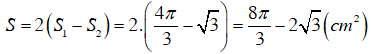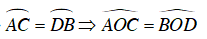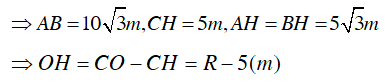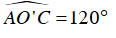Tính diện tích các hình liên quan đến diện tích hình tròn, hình quạt tròn | Toán lớp 9

Tính diện tích các hình liên quan đến diện tích hình tròn, hình quạt tròn

Với Tính diện tích các hình liên quan đến diện tích hình tròn, hình quạt tròn Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính diện tích các hình liên quan đến diện tích hình tròn, hình quạt tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

Sử dụng linh hoạt các kiến thức đã học để góc ở tâm, bán kính đường tròn. Từ đó sử dụng các công thức tính diện tích hình tròn và quạt tròn để tính diện tích hình cần tìm.

Áp dụng các công thức:

+ Công thức tính diện tích hình tròn: S = πR²

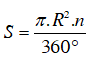
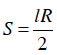
+ Công thức tính diện tích hình quạt tròn bán kính R, cung n^o : hay .

B. Ví dụ minh họa

Ví dụ 1 : Một đám cỏ hình tròn có đường kính 12m, bị cắt thành một lối đi thẳng rộng 3m để lát sỏi. Một cạnh của lối đi này là đường kính của đám cỏ. Tìm diện tích đám cỏ còn lại.

Hướng dẫn giải

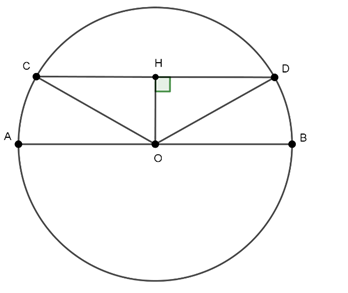
Ta có các dây AB, CD tạo thành lối đi

Vì AB//CD

OH là bề rộng của lối đi nên OH = 3m.

Đường kính đường tròn là 12m, nên bán kính là 6m

Xét ΔOHC vuông tại H, ta có:

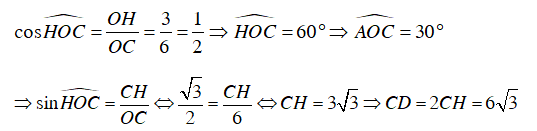
Diện tích ΔCOD là: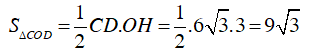

Diện tích hình quạt AOC là: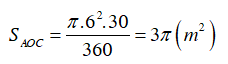

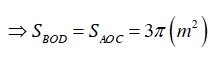
Diện tích lối đi: .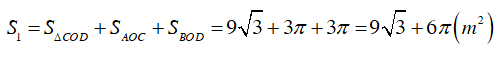

Diện tích hình tròn là: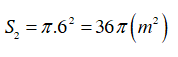

Diện tích đám cỏ còn lại là: .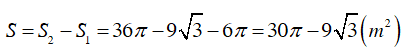

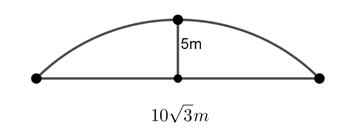
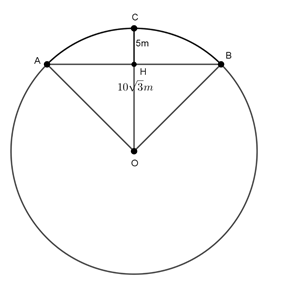
Ví dụ 2 : Một đường hầm có mặt cắt vuông góc là một phần đường tròn như hình bên. Mặt cắt này có chiều cao lớn nhất là 5m, chiều rộng 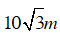. Tính diện tích mặt cắt của đường hầm.

Hướng dẫn giải

Gọi AB là dây cung tương ứng với chiều rộng của mặt cắt đường hầm, C là điểm trên cung nhỏ AB sao cho OC ⊥ AB, H là giao điểm của AB và OC. Khi đó, ta có: H là trung điểm của AB.

Xét ΔOAH vuông tại H, có: OA² = OH² + AH² ( định lý Py – ta – go)

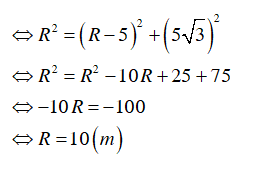
⇒ OH = 5 (m)

Ta lại có: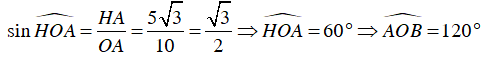

Diện tích hình quạt AOB là: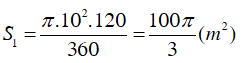

Diện tích tam giác AOB là: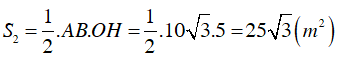

Khi đó diện tích mặt cắt hầm là: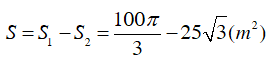

Ví dụ 3 : Cho hình thang ABCD (AD//BC) có: 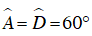và AD = 4cm. Cạnh BC là đường kính của nửa đường tròn nội tiếp (như hình vẽ). Tính diện tích phần nằm trong hình thang và nằm ngoài nửa hình tròn.

Hướng dẫn giải

Từ B hạ BK ⊥ AD, đặt AK = x

Xét ΔABK vuông tại K, ta có:

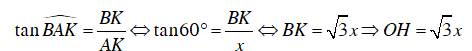
Vì H thuộc nửa đường tròn đường kính BC

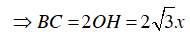
Mà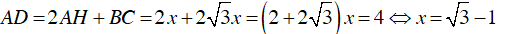

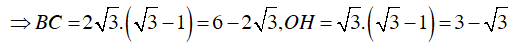
Diện tích hình thang ABCD là: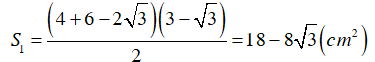

Diện tích nửa hình tròn đường kính BC là: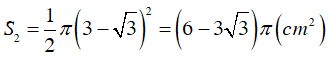

Diện tích hình cần tìm là: .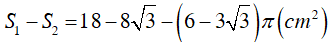

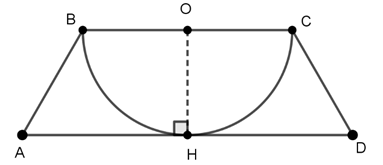
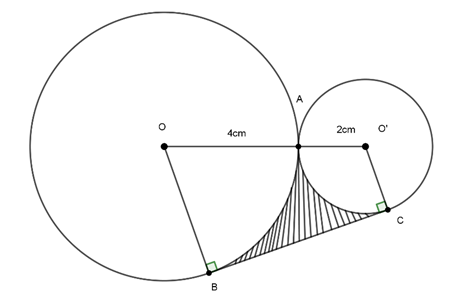
Ví dụ 4 : Cho hai đường tròn (O; 4cm) và (O’; 2cm) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài tiếp xúc (O) tại B và (O’) tại C. Tính diện tích phần gạch sọc biết BC = 5cm và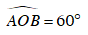

Hướng dẫn giải

Diện tích hình thang OO’CB là: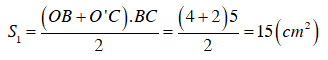

Diện tích hình quạt OAB là: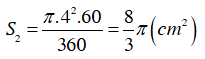

Vì O’C//OB ⇒ 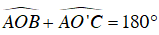(hai góc trong cùng phía bù nhau)

⇒

Diện tích hình quạt AO’C là: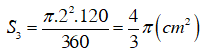

Diện tích phần gạch sọc: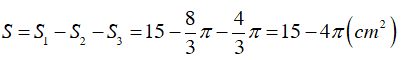

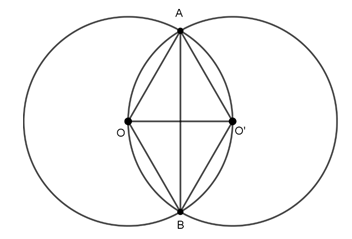
Ví dụ 5 : Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tâm O nằm trên đường tròn (O’) và tâm O’ nằm trên đường tròn (O). Biết 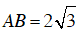cm. Tìm diện tích phần giao của hai đường tròn.

Hướng dẫn giải

Ta có: OA = OB = OO’ = O’A = O’B

⇒ (O) và (O’) bằng nhau, ΔOAO' ,ΔOBO' đều

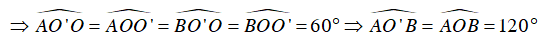
Gọi H là giao điểm của OO’ với AB

và

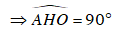
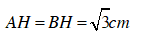
Xét tam giác AHO vuông tại H, ta có:

+

+

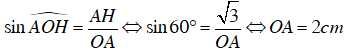
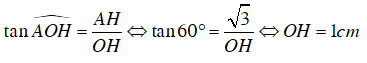
Diện tích hình quạt AO’B là :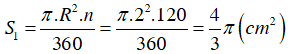

Diện tích hình tam giác AOB là :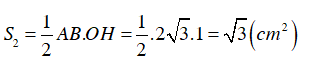

Diện tích cần tìm là : .