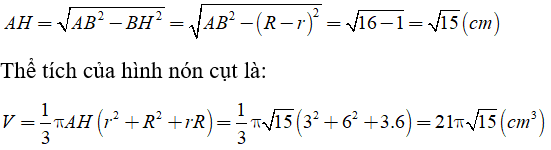Các dạng bài tập Toán 9 Chương 4 phần Hình học cực hay có đáp án | Toán lớp 9
Các dạng bài tập Toán 9 Chương 4 phần Hình học cực hay có đáp án
Với Các dạng bài tập Toán 9 Chương 4 phần Hình học cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 4 phần Hình học từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Lý thuyết & Trắc nghiệm theo bài học
- Lý thuyết Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ (hay, chi tiết)
- Trắc nghiệm Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
- Lý thuyết Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt (hay, chi tiết)
- Trắc nghiệm Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Lý thuyết Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu (hay, chi tiết)
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
- Tổng hợp lý thuyết Chương 4 Hình học 9 (hay, chi tiết)
- Tổng hợp Trắc nghiệm Chương 4 Hình học 9
Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
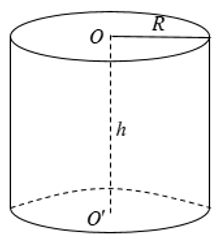
1. Hình trụ
Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.
+ Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.
+ Đường thẳng AB được gọi là trục của hình trụ.
+ Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.
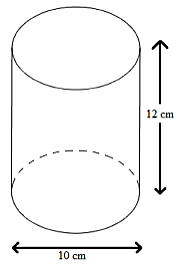
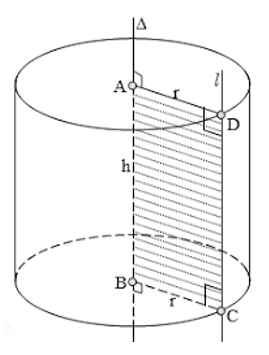
2. Cắt hình trụ bởi một mặt phẳng
+ Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.
+ Khi cắt hình trụ bởi một mặt phẳng song song với trục OO' thì mặt cắt là một hình chữ nhật
3. Diện tích và thể tích hình trụ
Cho hình trụ có bán kính đáy R và chiều cao h.
+ Diện tích xung quanh: Sxq = 2πRh
+ Diện tích toàn phần: Stp = 2πRh + 2πR2
+ Thể tích: V = πR2h
4. Ví dụ cụ thể
Câu 1: Một hình trụ có bán kính đáy bằng 1/4 đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là một hình chữ nhật có diện tích là 50cm2. Tính diện tích xung quanh và thể tích hình trụ.
Hướng dẫn:
Theo giả thiết ta có
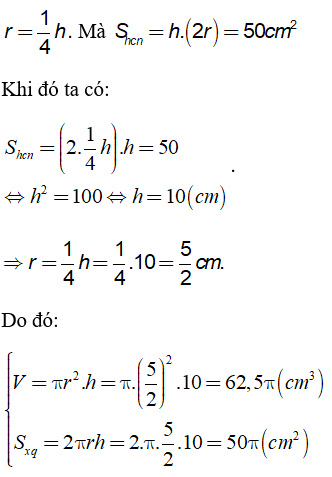
B. Bài tập tự luận
Câu 1: Tính diện tích xung quanh và diện tích toàn phần của hình sau
Lời giải:

Câu 2: Hình chữ nhật ABCD có AB = a, BC = 3a . Quay hình chữ nhật quanh cạnh AB thì được thể tích V1, quay quanh cạnh BC thì được thể tích V2. Tỉ số thể tích giữa V1 và V2 là?
Lời giải:

Lý thuyết Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
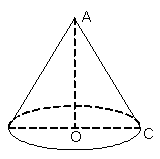
1. Hình nón
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.
+ Điểm A được gọi đỉnh của hình nón.
+ Hình tròn (O) được gọi là đáy của hình nón.
+ Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
+ Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích – thể tích của hình nón
Đặt AC = l; l là đường sinh
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
+ Diện tích xung quanh: Sxq = πRl
+ Diện tích toàn phần: Stp = πRl + πR2
+ Thể tích: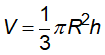
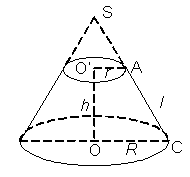
3. Hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.
+ Hai hình tròn (O) và (O') được gọi là hai đáy.
+ Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.
+ Đoạn AC được gọi là đường sinh.
4. Diện tích – thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
+ Diện tích xung qaunh: Sxq = π(R + r)l
+ Thể tích: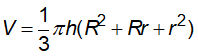
5. Ví dụ cụ thể
Câu 1: Một hình nón có bán kính đáy bằng và diện tích xung quanh là . Tính thể tích của hình nón đó.
Hướng dẫn:
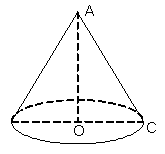
Ta có Sxq = πRl. Theo giả thiết ta có: Sxq = 65π (cm2) ⇒ πRl = 65π (cm2)
Khi đó ta có:
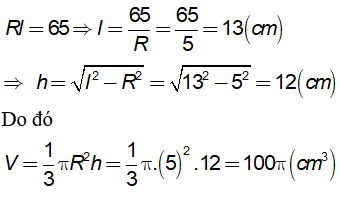
B. Bài tập tự luận
Câu 1: Cho hình nón như hình bên:
Biết rằng đáy là hình tròn có bán kính bằng 3cm, đường sinh có độ dài là 5cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón đó.
Lời giải:
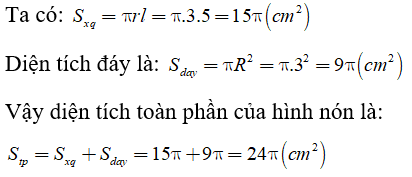
Muốn tính thể tích hình nón, ta cần biết chiều cao hạ từ đỉnh xuống đáy (hay khoảng cách từ đỉnh xuống tâm đường tròn)
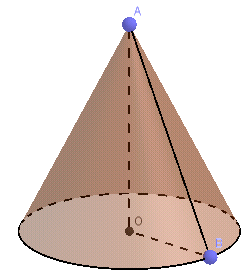
Xét tam giác AOB vuông tại O
Áp dụng định lý Pi – ta- go trong tam giác AOB ta có:
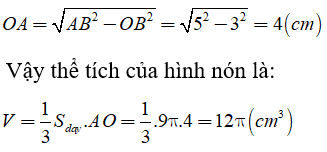
Câu 2: Cho hình nón cụt như hình vẽ
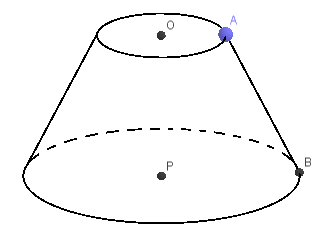
Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh và thể tích của hình nón cụt
Lời giải:
Diện tích xung quanh của hình nón cụt là:
Sxq = π(r + R)l = π(3 + 6).4 = 36π (cm2)
Để tính chiều cao hình nón cụt, ta có hình vẽ sau:
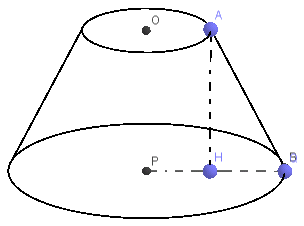
Áp dụng định lý Py – ta – go và tam giác AHB vuông tại H ta có: