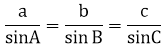Cách tính Tỉ số lượng giác của góc nhọn cực hay, có đáp án | Toán lớp 9
Cách tính Tỉ số lượng giác của góc nhọn cực hay, có đáp án
Với Cách tính Tỉ số lượng giác của góc nhọn cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tỉ số lượng giác của góc nhọn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Lý thuyết và Phương pháp giải
1. Định nghĩa
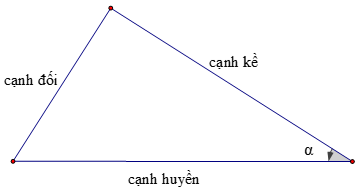

2. Định lí
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.
3. Một số hệ thức cơ bản
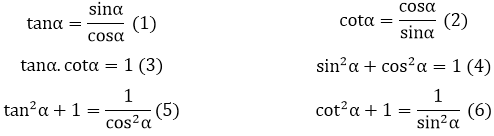
4. So sánh các tỉ số lượng giác
a) Cho α,β là hai góc nhọn. Nếu α < β thì
* sinα < sinβ; tanα < tanβ
*cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα

Ví dụ minh họa
Ví dụ 1: Cho ΔABC với 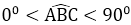
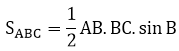
Hướng dẫn:
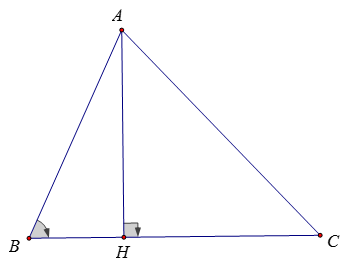
Kẻ AH vuông góc với BC, H ∈ BC
Ta có: SABC = 1/2.AH.BC (1)
Xét tam giác ABH vuông tại H có:
sinB = AH/AB ⇒ AH = AB.sinB (2)
Từ (1) và (2),ta có
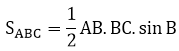
Ví dụ 2: Cho tam giác ABC, góc A bằng 600. Vẽ các đường cao AD và CE. Chứng minh rằng: BC = 2DE
Hướng dẫn:
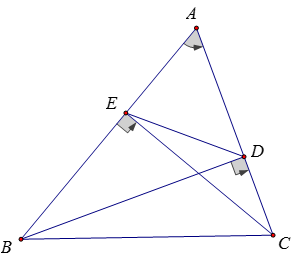
Ta có: ΔABD ~ ΔACE (g.g)
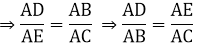
Xét ΔADE và ΔABC có:
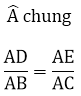
⇒ ΔADE ~ ΔABC (c.g.c)

Vậy BC = 2DE
Ví dụ 3: Chứng minh rằng giá trị cuả các biểu thức sau không phụ thuộc vào số đo của góc nhọn α
a) A = cos4α + 2cos2α.sin2α + sin4α
b) B = sin4α + cos2α.sin2α + cos2α
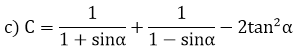
Hướng dẫn:
a) A = cos4 α + 2cos2 α.sin2 α + sin4 α
=(cos2 α + sin2 α)2 = 12 = 1
b) B = sin4 α + cos2 α.sin2 α + cos2 α
= sin2 α(sin2 α + cos2 α) + cos2 α
= sin2 α.1 + cos2 α = 1
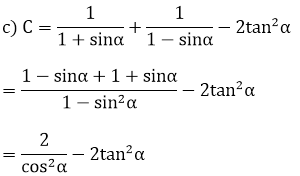
= 2(1 + tan2 α) - 2tan2 α = 2
Ví dụ 4: Không dùng bảng số hay máy tính , hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: cos 650; sin 200; cot 400, tan 480
Hướng dẫn:
Ta có: cos 650 = sin 250; cot 400 = tan 500
Sắp xếp: sin 200 < sin 250 < sin 480 < tan 480 < tan 500
Do đó: sin 200 < cos 650 < tan 480 < cot 400
Ví dụ 5: Chứng minh định lí sin: Trong tam giác nhọn, độ dài các cạnh tỉ lệ với sin của các góc đối diện:
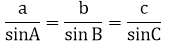
Hướng dẫn:
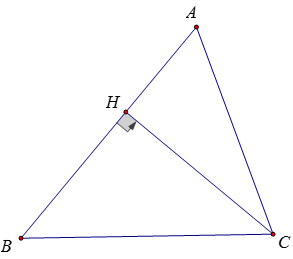
Vẽ đường cao CH, ta có:
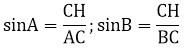
Do đó:
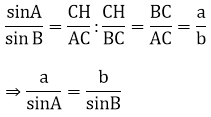
Chứng minh tương tự, ta có:
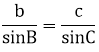
Vậy