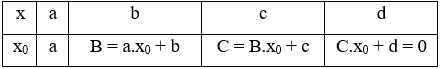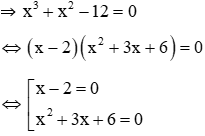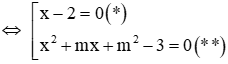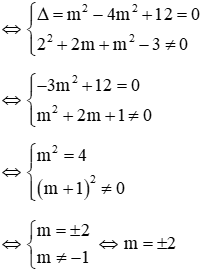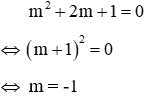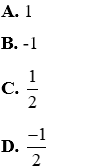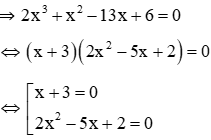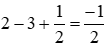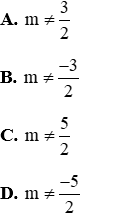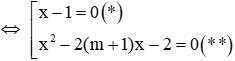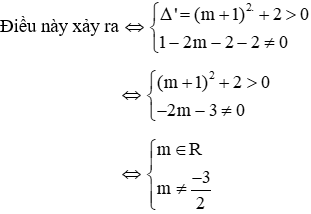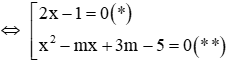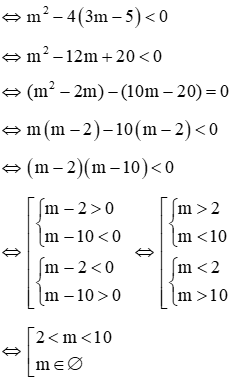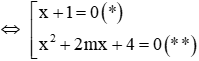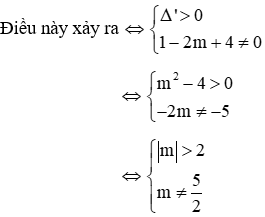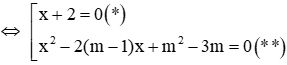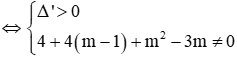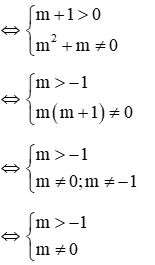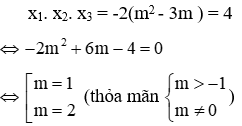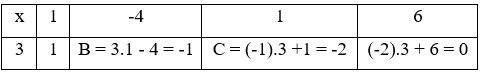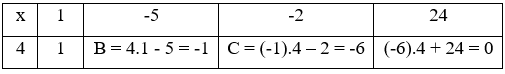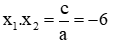Cách giải phương trình bậc ba có một nghiệm cho trước | Toán lớp 9

Cách giải phương trình bậc ba có một nghiệm cho trước

Với Cách giải phương trình bậc ba có một nghiệm cho trước Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình bậc ba có một nghiệm cho trước từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Bài toán: Cho phương trình ax³ + bx² + cx + d = 0 (a ≠ 0), biết phương trình có một nghiệm x ₀, tìm các nghiệm còn lại của phương trình

Cách giải:

- Nếu x = x ₀ là nghiệm của phương trình ax³ + bx² + cx + d = 0 thì

ax³ + bx² + cx + d = (x - x ₀).f(x)

- Để tìm f(x) ta lấy đa thức ax³ + bx² + cx + d chia cho (x - x ₀).

- Giả sử f(x) = ax² + Bx + C, khi đó phương trình ax³ + bx² + cx + d = 0 được đưa về phương trình dạng tích (x - x ₀). (ax² + Bx + C) = 0

Chú ý: để tìm f(x) ngoài cách chia đa thức ta có thể sử dụng sơ đồ Hooc-ne sau

Khi đó: ax³ + bx² + cx + d = (x - x ₀).(ax² + Bx + C)

Ví dụ 1: Tìm các nghiệm của phương trình x³ + x² = 12 (1), biết x = 2 là một nghiệm của phương trình

Giải

Phương trình (1) ⇔ x³+x²-12 = 0

Vì x = 2 là một nghiệm của phương trình nên lấy đa thức (x³ + x² – 12) chia cho

(x – 2). Ta sử dụng sơ đồ Hooc-ne để chia:

Vậy x³ + x² – 12 = (x – 2).( x² + 3x + 6)

Xét phương trình: x – 2 = 0 ⇔ x = 2

Xét phương trình: x² + 3x + 6 = 0 có ∆ = 3² - 4.1.6 = -15 < 0 nên phương trình vô nghiệm

Vây phương trình có nghiệm duy nhất x = 2

Ví dụ 2: Tìm m để phương trình: (x - 2)(x² + mx+ m² – 3) = 0 (1) có đúng 2 nghiệm phân biệt

Giải

Phương trình (1)

Phương trình (*) có 1 nghiệm x = 2 nên để phương trình (1) có đúng 2 nghiệm thì phương trình (**) phải có nghiệm kép khác 2 hoặc có 2 nghiệm phân biệt trong đó một nghiệm bằng 2

+ TH1: phương trình (**) có nghiệm kép khác 2 ⇔ phương trình (**) có

∆ = 0 và x = 2 không là nghiệm của (**)

+ TH2: phương trình (**) có 2 nghiệm phân biệt trong đó một nghiệm bằng 2

Thay x = 2 vào phương trình (**) ta được:

Với m = -1 thì phương trình (**) trở thành: x²-x-2 = 0

Phương trình này có a – b + c = 0 nên có 2 nghiệm x = -1, x = 2

Suy ra m = -1 thỏa mãn

Vậy m = -1, m = 2, m = -2 là các giá trị cần tìm

B. Bài tập

Câu 1: Tính tổng các nghiệm của phương trình, biết x = -3 là một nghiệm của phương trình

Giải

Vì x = -3 là một nghiệm của phương trình nên ta lấy đa thức (2x³ + x² – 13x + 6)chia cho (x + 3). Ta sử dụng sơ đồ Hooc-ne để chia

Vậy 2x³ + x² – 13x + 6 = (x + 3).(2x² - 5x + 2)

Xét phương trình x + 3 = 0 ⇔ x = -3

Xét phương trình 2x² - 5x + 2 = 0 có ∆ = (-5)² - 4.2.2 = 9 > 0 nên phương trình có hai nghiệm phân biệt: x = 2, x = 1/2

Vậy tổng các nghiệm của phương trình là:

Đáp án là D

Câu 2: Tìm m để phương trình (x - 1)(x² – 2(m + 1)x – 2) = 0 (1) có 3 nghiệm phân biệt

Giải

Phương trình (1)

Phương trình (*) có 1 nghiệm x = 1 nên để phương trình (1) có 3 nghiệm phân biệt thì phương trình (**) phải có 2 nghiệm phân biệt khác x = 1

Vậy với 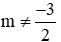thì phương trình có 3 nghiệm phân biệt

Đáp án là B

Câu 3: Tìm m để phương trình (2x - 1)(x² – mx + 3m - 5) = 0 (1) có đúng 1 nghiệm

A. 1 < m < 8

B. 2 < m < 10

C. m = 4

D. m = 0

Giải

Phương trình (1)

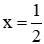
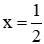
Phương trình (*) có 1 nghiệm nên để phương trình (1) có đúng 1 nghiệm thì phương trình (**) phải có nghiệm kép hoặc vô nghiệm

+ TH1: phương trình (**) có nghiệm kép

Thay 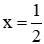vào phương trình (**) ta được:

+ TH2: phương trình (**) vô nghiệm ⇔ ∆ < 0

Vậy 2 < m < 10 là các giá trị cần tìm

Đáp án là B

Câu 4: Tìm m để phương trình (x + 1)(x² + 2mx + 4) = 0 (1) có 3 nghiệm phân biệt và tổng các nghiệm bằng 3

A. m = 1

B. m = 6

C. Không tồn tại m

D. m = 0

Giải

Phương trình (1)

Phương trình (*) có 1 nghiệm x₁ = -1 nên để phương trình (1) có 3 nghiệm thì phương trình (**) phải có 2 nghiệm phân biệt x₂, x₃ khác x₁ = -1

Vì x₂, x₃ là hai nghiệm của phương trình (**) nên x₂ + x₃ = -2m

Tổng các nghiệm của phương trình (1) là: x₁ + x₂ + x₃ = -1 – 2m = 3 ⇔ m = -2

m = -2 không thỏa mãn điều kiện 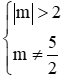nên loại

Vậy không có giá trị nào của m thỏa mãn đề bài

Đáp án là C

Câu 5: Tìm m để phương trình (x + 2)(x² – 2(m-1)x + m² – 3m) = 0 (1) có 3 nghiệm phân biệt và tích các nghiệm bằng 4

A. m = 1

B. m = 1, m = 2

C. m = 2

D. m = 0

Giải

Phương trình (1)

Phương trình (*) có 1 nghiệm x₁ = -2 nên để phương trình (1) có 3 nghiệm thì phương trình (**) phải có 2 nghiệm phân biệt x₂, x₃ khác x₁ = -2

Điều này xảy ra

Vì x₂, x₃ là hai nghiệm của phương trình (**) nên x₂. x₃ = m² - 3m

Tích các nghiệm của phương trình (1) là:

Vậy với m = 1, m = 2 thì phương trình (1) có nghiệm thỏa mãn yêu cầu đặt ra

Đáp án đúng là B

Câu 6: Biết rằng phương trình x³ – 4x² + x + 6 = 0 được đưa về phương trình

(x -3)(x² + Bx + C) = 0. Hãy tính B + C

A. -5

B. -4

C. -6

D. -3

Giải

Dùng sơ đồ Hooc-ne chia đa thức x³ – 4x² + x + 6 cho x – 3

Vậy x³ - 4x² + x + 6 = (x - 3).(x² - x - 2)

Suy ra phương trình x³ – 4x² + x + 6 = 0 ⇔ (x - 3).(x² - x - 2) = 0

Vậy B = -1 và C = -2 ⇒ B + C = -1 – 2 = -3

Đáp án D

Câu 7: Biết rằng phương trình x³ – 5x² - 2x + 24 = 0 được đưa về phương trình (x - 4)(x² + Bx + C) = 0. Hãy tính tích các nghiệm của phương trình x² + Bx + C = 0 nếu có

A. -6

B. -7

C. -8

D. -9

Giải

Dùng sơ đồ Hooc-ne chia đa thức x³ – 5x² - 2x + 24 cho x – 4

Vậy x³ - 5x² - 2x + 24 = (x - 4).(x² - x - 6)

Suy ra phương trình x² + Bx + C = 0 là phương trình x² - x – 6 = 0

Phương trình này có Δ = (-1)² - 4.(-6) = 25 > 0 nên có hai nghiệm phân biệt

Theo Vi-et tích các nghiệm của phương trình là

Đáp án A