Cách biến đổi đơn giản biểu thức chứa căn bậc hai cực hay, có đáp án | Toán lớp 9

Cách biến đổi đơn giản biểu thức chứa căn bậc hai cực hay, có đáp án

Với Cách biến đổi đơn giản biểu thức chứa căn bậc hai cực hay, có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập biến đổi đơn giản biểu thức chứa căn bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Lý thuyết và Phương pháp giải

    1. Đưa thừa số ra ngoài dấu căn

    với B ≥ 0

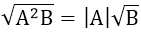
    2. Đưa thừa số vào trong dấu căn

    với A ≥ 0; B ≥ 0

    với A < 0; B ≥ 0

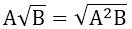
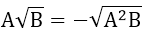
    3. Khử mẫu ở biểu thức chứa căn

    với AB ≥ 0; B ≠ 0

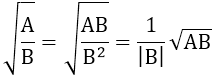
    4. Trục căn thức ở mẫu

    (A ≥ 0; B ≥ 0; A ≠ B)

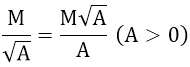
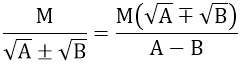
    5. Rút gọn biểu thức có chứa căn bậc hai

    Bước 1: Dùng các phép biến đổi đơn giản để đưa các căn thức bậc hai phức tạp thành căn thức bậc hai đơn giản.

    Bước 2: Thực hiện các phép tính theo thứ tự đã biết.

Ví dụ minh họa

Ví dụ 1: Sắp xếp các số sau theo thứ tự tăng dần:

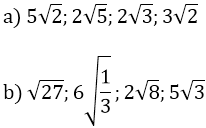
Hướng dẫn:

    a) Đưa thừa số vào trong dấu căn ta được:

    5√2 = √50; 2√5 = √20; 2√3 = √12; 3√2 = √18

    Mà √12 < √18 < √20 < √50

    ⇒ 2√3 < 3√2 < 2√5 < 5√2

    b) Đưa thừa số vào trong dấu căn ta được:

    6√(1/3) = √12; 2√8 = √32; 5√3 = √75

    Mà √12 < √27 < √32 < √75

    ⇒ 6√(1/3) < √27 < 2√8 < 5√3

    Nhận xét: Khi so sánh các căn thức với nhau, ta nên đưa các thừa số vào trong dấu căn, sau đó mới so sánh.

Ví dụ 2: Tính:

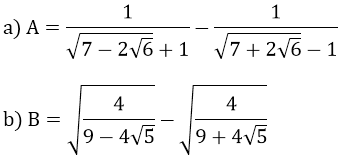
Hướng dẫn:

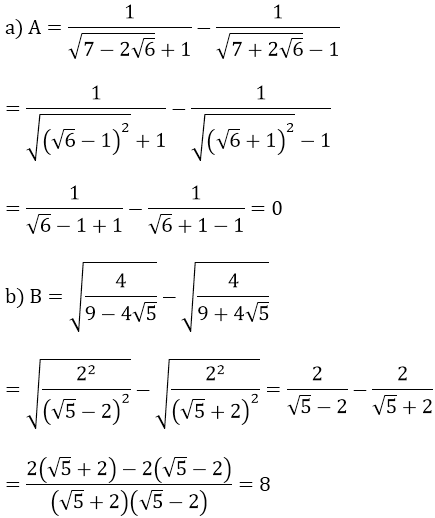
Ví dụ 3: Chứng minh đẳng thức sau:

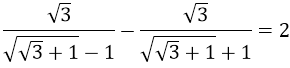
Hướng dẫn:

    Biến đổi vế trái, ta được:

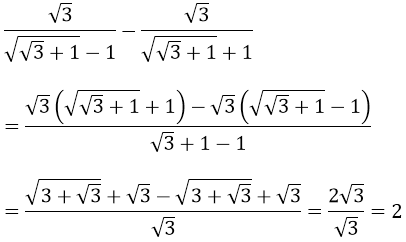
    Vế trái bằng vế phải, ta được điều phải chứng minh.

Ví dụ 4:Cho:

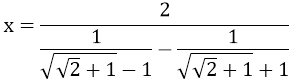
    Tính giá trị của biểu thức A = (x⁴ - x³ - x² + 2x - 1)²⁰¹⁸

Hướng dẫn:

    Biến đổi biểu thức ở mẫu của x, ta được:

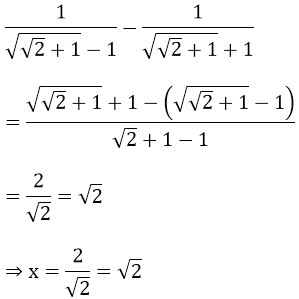
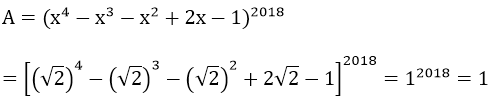
Ví dụ 5: Cho biểu thức:

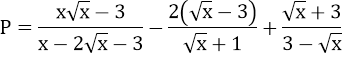
    a) Rút gọn P

    b) Tính giá trị của P với x = 14 - 6√5

    c) Tìm giá trị nhỏ nhất của biểu thức P

Hướng dẫn:

    a) ĐKXĐ: x ≥ 0; x ≠ 9. Ta có:

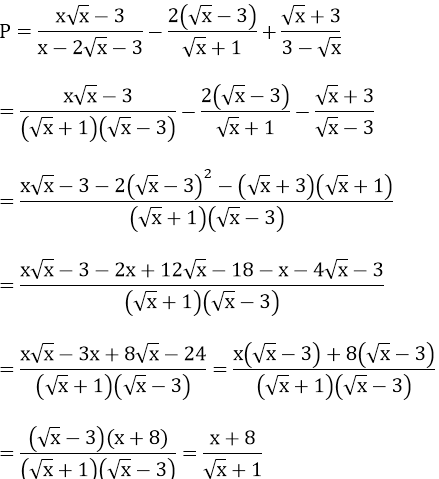
    b) x = 14 - 6√5 = (3 - √5)² thỏa mãn ĐKXĐ. Thay vào ta có:

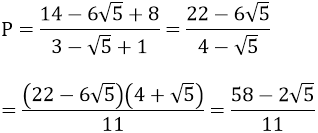
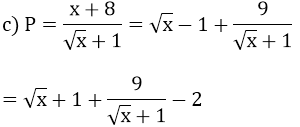
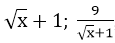
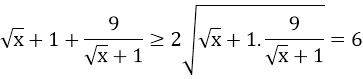
    Áp dụng bất đẳng thức Cauchy cho 2 số không âm , ta có:

    ⇒ P ≥ 6 - 2 = 4

    Dấu bằng xảy ra khi:

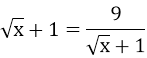
    ⇒ (√x + 1)² = 9 ⇒ √x + 1 = 3 ⇒ x = 4

    Vậy giá trị nhỏ nhất của P là 4, đạt được khi x = 4