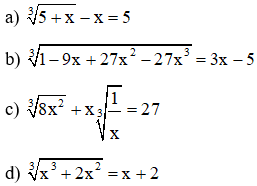Các dạng toán về Căn bậc ba và cách giải | Toán lớp 9
Các dạng toán về Căn bậc ba và cách giải
Với Các dạng toán về Căn bậc ba và cách giải Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Căn bậc ba từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
I. Lý thuyết
1. Căn bậc ba
Căn bậc ba của một số thực a là số x sao cho x3 = a kí hiệu là 3√a .
*Mọi số a đều có một căn bậc ba duy nhất.
*Căn bậc ba của số âm là số âm, căn bậc ba của số 0 là số 0, căn bậc ba của số dương là số dương.
2. Các công thức liên quan đến căn bậc ba
* A < B ⇔ 3√A < 3√B
* 3√A = 3√B ⇔ A = B
* 3√AB = 3√A.3√B
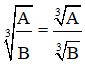với B ≠ 0
3. Trục căn thức bậc ba
Sử dụng các hằng đẳng thức:
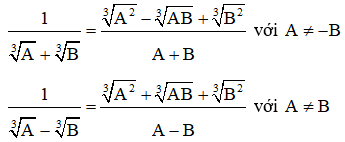
II. Các dạng bài tập.
Dạng 1: Thực hiện phép tính chứa căn bậc ba.
Phương pháp giải: Áp dụng công thức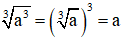 
Ví dụ: Thực hiện phép tính
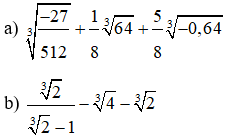
Lời giải:
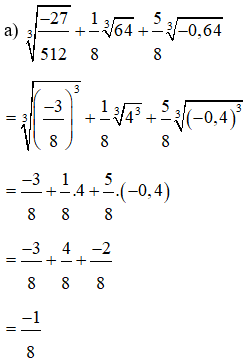
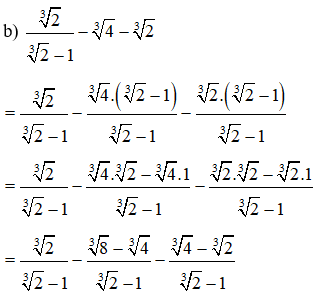
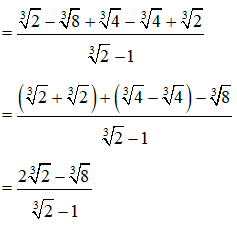
Dạng 2: Rút gọn biểu thức:
Phương pháp giải: Sử dụng hằng đẳng thức liên quan đến căn bậc ba:
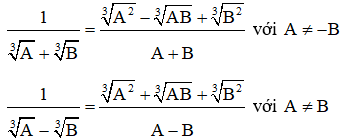
Ví dụ: Rút gọn biểu thức sau:
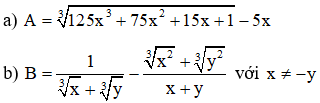
Lời giải:
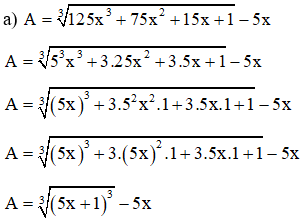
A = (5x + 1) - 5x
A = 5x + 1 - 5x
A = 1
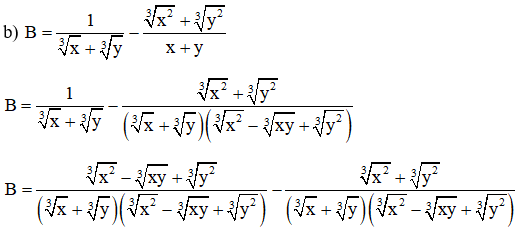
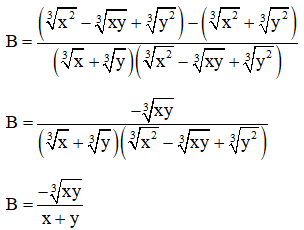
Dạng 3: So sánh căn bậc ba:
Phương pháp giải: Áp dụng lí thuyết
A < B ⇔ 3√A < 3√B
Ví dụ 1: So sánh
a) 7 và 23√43
b) A =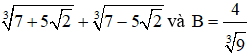 
Lời giải:
a) Ta có:
73 = 343
23√43 =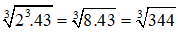 
Vì 343 < 344
=> 3√343 < 3√344
=> 7 < 23√43
Vậy 7 < 23√43
b) Ta có:
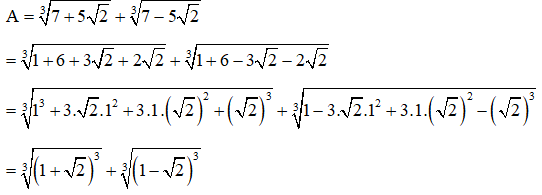
= 1 + √2 + 1 - √2
= 2
Ta có:
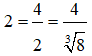
Vì 8 < 9 => 3√8 < 9√9
=> 
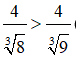(phân số nào có mẫu số lớn hơn thì bé hơn)
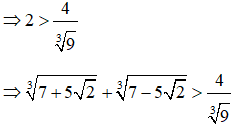
=> A > B
Dạng 4: Giải phương trình căn bậc ba.
Phương pháp giải:
Áp dụng: 3√A = B ⇔ A = B3
Chú ý: Căn bậc ba không có điều kiện trong căn như căn bậc hai
Ví dụ: Giải các phương trình sau:
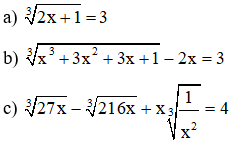
Lời giải:
a)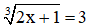 
⇔ 2x + 1 = 33
⇔ 2x + 1 = 27
⇔ 2x = 27 - 1
⇔ 2x = 26
⇔ x = 26 : 2
⇔ x = 13
Vậy nghiệm của phương trình là S =
b)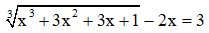 
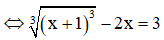
⇔ x + 1 - 2x = 3
⇔ -x = 3 -1
⇔ -x = 2
⇔ x = -2
Vậy phương trình có nghiệm là S = {-2}
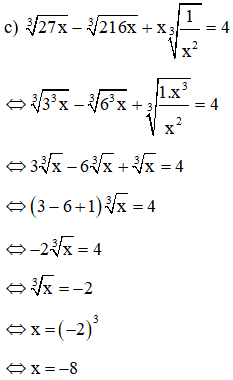
Vậy phương trình có nghiệm S = {-8}
III. Bài tập tự luyện
Bài 1: Thực hiện phép tính:
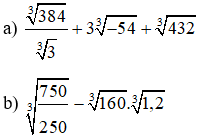
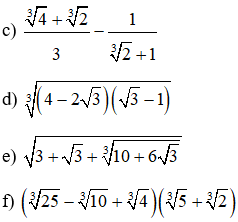
Bài 2: Rút gọn biểu thức:
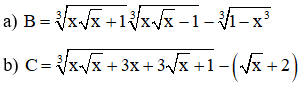
Bài 3: So sánh
a) 6 và 23√26
b) 33√2 và 3√53
c)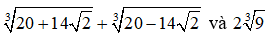 
Bài 4: Tìm x
