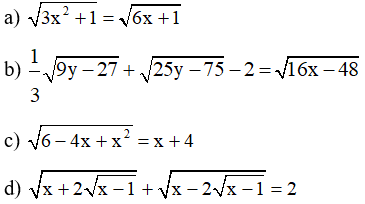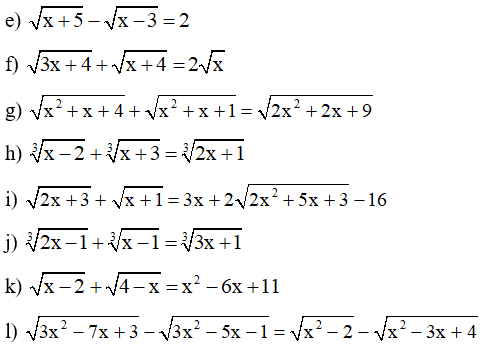Phương pháp Giải phương trình chứa dấu căn cực hay | Toán lớp 9
Phương pháp Giải phương trình chứa dấu căn cực hay
Với Phương pháp Giải phương trình chứa dấu căn cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giải phương trình chứa dấu căn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
I. Lý thuyết.
Một số phương pháp giải.
+ Biến đổi tương đương
+ Đưa về phương trình chứa dấu giá trị tuyệt đối
+ Đặt ẩn phụ
+ Nâng lũy thừa
+ Dùng bất đẳng thức đánh giá.
Một số phương trình căn bậc 2 thường gặp.
II. Dạng bài tập:
Dạng 1: Biến đổi tương đương
Phương pháp giải: Sử dụng các phép biến đổi khai căn, đưa thừa số vào trong căn hoặc ngoài dấu căn để giải phương trình.
Phương trình có dạng:
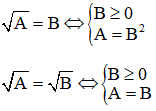
Ví dụ
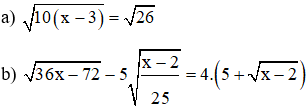
Lời giải:
a)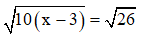 
Điều kiện: x ≥ 3
Phương trình đã cho ⇔ 10(x - 3) = 26
⇔ 10x - 30 = 26
⇔ 10x = 26 + 30
⇔ 10x = 56
⇔ x = 56 : 10
⇔ x =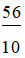 
(thỏa mãn)
Vậy phương trình có nghiệm S = {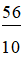
}
b)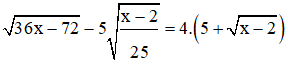 
Điều kiện: x ≥ 2
Phương trình đã cho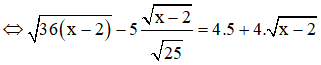 
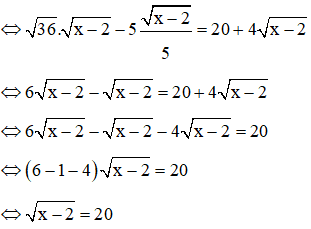
⇔ x - 2 = 400
⇔ x = 402
Vậy phương trình có nghiệm S =
Dạng 2: Đưa về phương trình chứa dấu giá trị tuyệt đối
Phương pháp giải: Sử dụng các công thức biến đổi để đưa phương trình về dạng
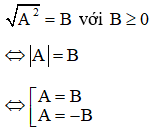
Ví dụ: Giải phương trình sau: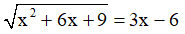 
Lời giải:
Điều kiện: 3x - 6 ≥ 0 ⇔ 3x ≥ 6 ⇔ x ≥ 2
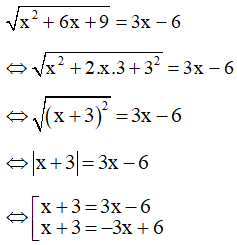
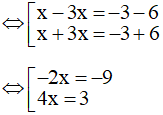
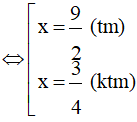
Vậy nghiệm của phương trình S =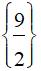 
Dạng 3: Đặt ẩn phụ
Phương pháp giải: Đặt ẩn thành một ẩn mới, khi đó phương trình sẽ được đưa về biến mới có thể giải bằng các phương pháp như biến đổi tương đương, trị tuyệt đối.
Ví dụ: Giải phương trình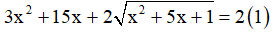 
Lời giải:
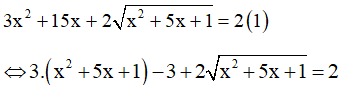
Đặt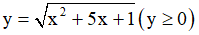 
Khi đó phương trình trở thành
3y2 + 2y - 3 - 2 = 0
⇔ 3y2 + 2y - 5 = 0
⇔ 3y2 - 3y + 5y - 5= 0
⇔ 3y(y - 1) + 5(y - 1) = 0
⇔ (y - 1)(3y + 5) = 0
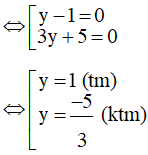
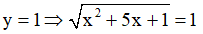
⇔ x2 + 5x + 1 = 1
⇔ x2 + 5x + 1 - 1 = 0
⇔ x2 + 5x = 0
⇔ x(x + 5) = 0
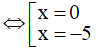
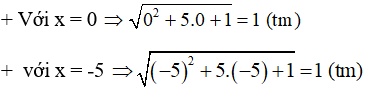
Vậy phương trình đã cho có nghiệm S = {-5,0}
Dạng 4: Đánh giá phương trình
Phương pháp giải: Sử dụng các phép đánh giá đã biết để đánh giá 2 về phương trình để suy ra trường hợp dấu bằng xảy ra.
Ví dụ: Giải phương trình sau: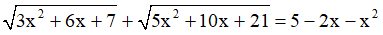 
Lời giải:
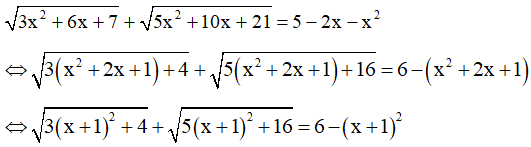
Ta có:
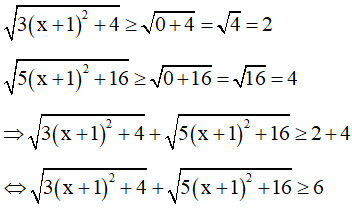
Lại có:
6 - (x - 1)2 ≤ 6
Dấu bằng xảy ra để vế trái bằng vế phải là
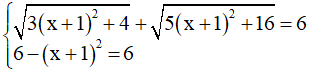
=> (x - 1)2 = 0
⇔ x + 1 = 0
⇔ x = -1
Vậy nghiệm của phương trình là S = {-1}
III. Bài tập vận dụng
Giải các phương trình sau
