Lý thuyết Cung chứa góc hay, chi tiết | Toán lớp 9

Lý thuyết Cung chứa góc hay, chi tiết

Tài liệu Lý thuyết Cung chứa góc hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Cung chứa góc từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Quỹ tích cung chứa góc

Với đoạn thẳng AB và góc α (0 < α < 180°) cho trước thì quỹ tích các điểm M thoả mãn ∠AMB = a là hai cung chứa góc α dựng trên đoạn AB.

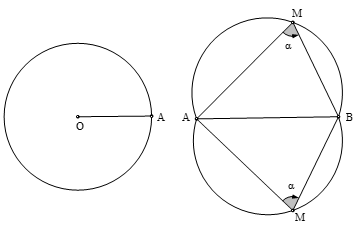
Chú ý:

    + Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB.

    + Hai điểm A, B được coi là thuộc quỹ tích.

    + Đặc biệt: Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

2. Cách vẽ cung chứa góc α

– Vẽ đường trung trực d của đoạn thẳng AB.

– Vẽ tia Ax tạo với AB một góc α.

– Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d.

– Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.

- được vẽ như trên là một cung chứa góc α.

3. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm M thoả mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:

– Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.

– Phần đảo: Mọi điểm thuộc hình H đều có tính chất T.

– Kết luận: Quỹ tích các điểm M có tính chất T là hình H.

4. Ví dụ

Ví dụ 1: Từ điểm M nằm bên ngoài đường tròn (O), kẻ cát tuyến MAB đi qua O và các tiếp tuyến MC, MD. Gọi K là giao điểm của AC và BD. Chứng mình rằng: 4 điểm B, C, M, K thuộc cùng một đường tròn.

Hướng dẫn: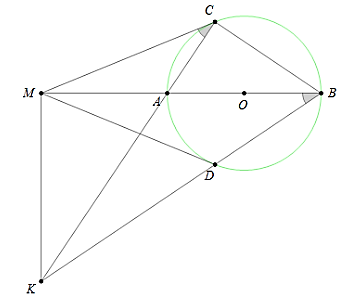

Ta đã biết MO là đường trung trực của CD nên AB là đường trung trực của CD

Suy ra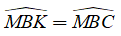

Mặt khác 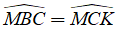(góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung CA)

Do đó: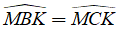

Tứ giác MCBK có 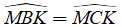nên M, C, B, K cùng thuộc một đường tròn

Ví dụ 2: Cho hình bình hành ABCD (AB // CD) , O là giao điểm của hai đường chéo. Trên tia OA lấy điểm M sao cho OM = OB. Trên tia OB lấy điểm N sao cho ON = OA. Chứng minh rằng: 4 điểm D, M, N, C cùng thuộc một đường tròn.

Hướng dẫn: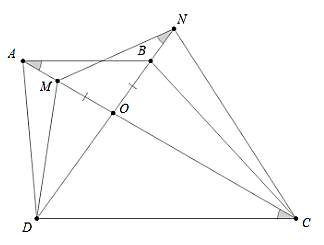

B. Bài tập tự luận

Câu 1: Cho cung AB cố định tạo bởi các bán kính OA, OB vuông góc với nhau, điểm I chuyển động trên cung AB. Trên tia OI lấy điểm M sao cho OM bằng tổng các khoảng cách từ I đến OA và OB. Tìm quỹ tích các điểm M.

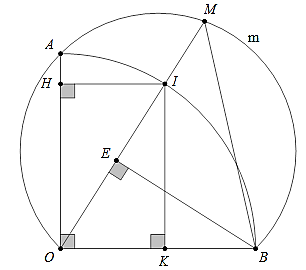
Lời giải:

Kết luận: Quỹ tích (tập hợp) điểm M là cung AmB, một phần của cung chứa góc 45° dựng trên OB nằm bên trong góc vuông AOB.

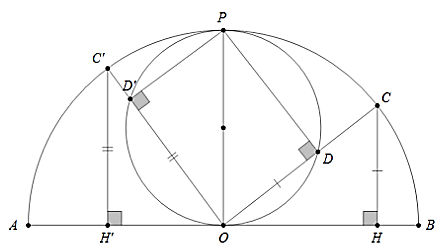
Câu 2: Cho nửa đường tròn (O) đường kính AC. C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách từ C đến AB.

Lời giải:

Kết luận: Quỹ tích (tập hợp) các điểm D khi C chạy trên nửa đường tròn đường kính AB là đường tròn đường kính OP với P là điểm chính giữa cung AB.