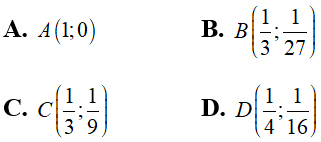Bài tập Đồ thị hàm số y = ax2 (a ≠ 0) chọn lọc, có đáp án | Toán lớp 9

Bài tập Đồ thị hàm số y = ax2 (a ≠ 0) chọn lọc, có đáp án

Với Bài tập Đồ thị hàm số y = ax2 (a ≠ 0) chọn lọc, có đáp án Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đồ thị hàm số y = ax2 (a ≠ 0) từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Đồ thị hàm số y = 1/3 x² đi qua điểm nào sau đây?

Lời giải:

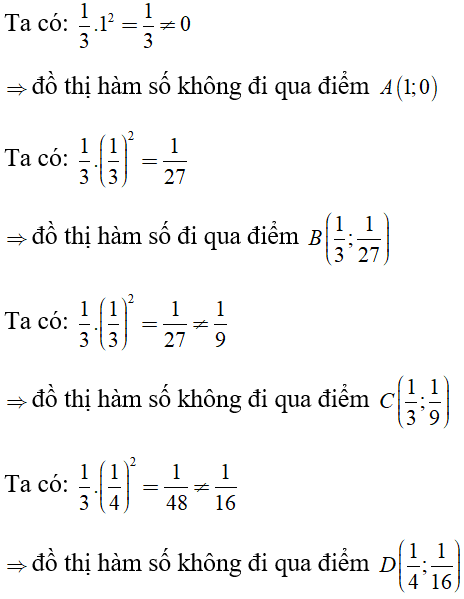
Chọn đáp án B.

Câu 2: Tọa độ giao điểm của đồ thị hàm số y = x² với đường thẳng y = 4x - 3 là?

A. (-1; 1), (3; 9)

B. (-1; 1), (-3; 9)

C. (1; 1), (3; 9)

D. (1; 1), (-3; 9)

Lời giải:

Phương trình hoành độ giao điểm là:

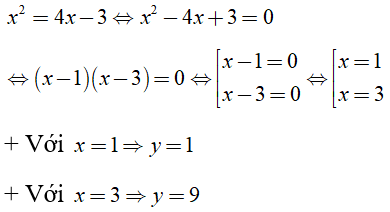
Do đó tọa độ giao điểm là (1; 1), (3; 9)

Chọn đáp án C.

Câu 3: Số giao điểm của đồ thị hàm số y = 4x² với đường thẳng y = 4x - 3

A. 1

B. 0

C. 2

D. 3

Lời giải:

Phương trình hoành độ giao điểm:

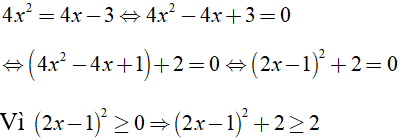
Khi đó phương trình hoành độ giao điểm trên vô nghiệm.

Vậy không có giao điểm nào

Chọn đáp án B.

Câu 4: Trên mặt phẳng tọa độ cho điểm A( 1; 2) thuộc đồ thị hàm số y = ax² (a ≠ 0).

Hỏi điểm nào thuộc đồ thị hàm số ?

A. M (2; 8)

B. N ( -2; 4)

C. P( - 3; 9)

D. Q( 4; 16)

Lời giải:

Vì điểm A(1; 2) thuộc đồ thị hàm số y = ax² (a ≠ 0) nên:

2 = a.1² ⇒ a = 2

Vây hàm số đã cho là y = 2x².

Trong các điểm đã cho chỉ có điểm M (2; 8) thuộc đồ thị hàm số .

Chọn đáp án A.

Câu 5: Biết đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm A(1; a). Hỏi có bao nhiêu giá trị của a thỏa mãn?

A. 1

B.2

C. 0

D. Vô số

Lời giải:

Do đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm A(1; a) nên:

a = a.1² ⇔ a = a ( luôn đúng với mọi a khác 0).

Vậy có vô số giá trị của a thỏa mãn.

Chọn đáp án D.

Câu 6: Cho đồ thị hàm số y = -2x². Tìm các điểm thuộc đồ thị hàm số đã cho có tung độ - 8.

A. (2; -8)

B. (-2; -8)

C. Cả A và B đúng

D. Tất cả sai

Lời giải:

Các điểm thuộc đồ thị hàm số đã cho có tung độ bằng -8 thỏa mãn:

-8 = -2x² ⇔ x² = 4 ⇔ x = ±2

Vậy có 2 điểm thuộc đồ thị hàm số đã cho có tung độ bằng -8 là M (-2; - 8) và N(2; -8)

Chọn đáp án C.

Câu 7: Cho y = ax² (a ≠ 0) đồ thị hàm số . Với giá trị nào của a thì đồ thị của hàm số đã cho nằm phía trên trục hoành.

A. a < 0

B. a > 0

C.

D. a > 2

Lời giải:

Đồ thị hàm số y = ax² (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.

+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.

+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.

Do đó, để đồ thị hàm số đã cho nằm phía trên trục hoành thì a > 0.

Chọn đáp án B.

Câu 8: Cho đồ thị của các hàm số sau:

(1): y = - 2x²      (2): y = x²      (3): y = -3x²      (4): y = -10x²

Hỏi có bao nhiêu đồ thị hàm số nằm phía dưới trục hoành?

A. 1

B. 2

C. 3

D. 4

Lời giải:

Đồ thị hàm số y = ax² (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.

+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.

+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.

Trong đồ thị các hàm số đã cho; các đồ thị nằm phía dưới trục hoành là”

(1): y = -2x²; (3): y = - 3x² và (4):y = -10x²

Chọn đáp án C.

Câu 9: Cho đồ thị hàm số y = 3x². Tìm tung độ của điểm thuộc parabol có hoành độ là số nguyên dương nhỏ nhất?

A. 0

B. 1

C. -3

D. 3

Lời giải:

Số nguyên dương nhỏ nhất là 1.

Do đó, tung độ của điểm thuộc parabol có hoành độ 1 là: y = 3.1² = 3

Chọn đáp án D.

Câu 10: Cho đồ thị hàm số y = x² và y = 3x². Tìm giao điểm của hai đồ thị hàm số đã cho?

A. O(0; 0)

B. A(1; 1)

C. O(0; 0) và A(1; 1)

D. O(0; 0) và B( 1; 3)

Lời giải:

Hoành độ giao điểm của hai đồ thị hàm số đã cho là nghiệm phương trình:

x² = 3x² ⇔ -2x² = 0 ⇔ x = 0

Với x = 0 thì y= 0² = 0

Do đó,đồ thị hai hàm số đã cho cắt nhau tại điểm duy nhất là gốc tọa độ O(0; 0).

Chọn đáp án A.