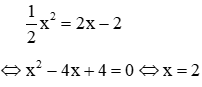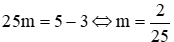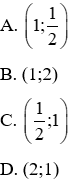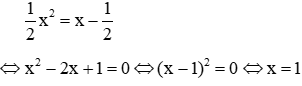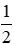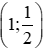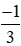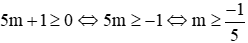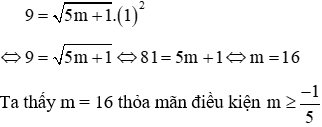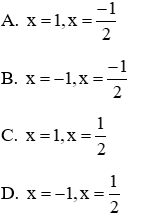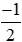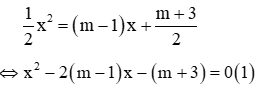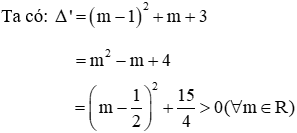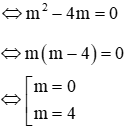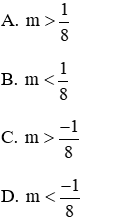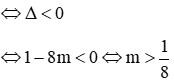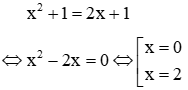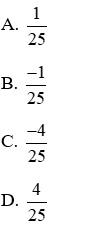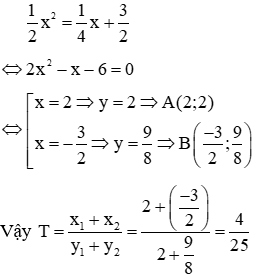Cách tìm giao điểm của parabol P và đường thẳng hay, chi tiết | Toán lớp 9

Cách tìm giao điểm của parabol P và đường thẳng hay, chi tiết

Với Cách tìm giao điểm của parabol P và đường thẳng hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm giao điểm của parabol P và đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Bài toán: Cho parabol (P) y = ax² (a ≠ 0) và đường thẳng y = kx + b. Tìm giao điểm của (P) và đường thẳng

Cách giải:

- Lập phương trình hoành độ giao điểm: ax² = kx + b (1)

- Số nghiệm của phương trình (1) là số giao điểm của (P) và đường thẳng

- Thay nghiệm x của phương trình (1) vào công thức của đường thẳng hoặc của (P) tìm y. Khi đó tọa độ giao điểm của (P) và đường thẳng là (x;y)

Ví dụ 1: Cho parabol (P) 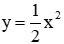và đường thẳng y = 2x - 2. Tìm giao điểm của (P) và đường thẳng

Giải

Phương trình hoành độ giao điểm:

Thay x = 2 vào phương trình đường thẳng y = 2x – 2 ta được y = 2

Vậy (P) cắt đường thẳng tại một điểm A(2;2)

Ví dụ 2: Cho hàm số y = mx² có đồ thị là parabol (P). Tìm m biết rằng (P) cắt đường thẳng y = x – 3 tại điểm có hoành độ bằng 5

Giải

Phương trình hoành độ giao điểm: mx² = x – 3 (1)

Vì (P) cắt đường thẳng y = x – 3 tại điểm có hoành độ bằng 5 nên x = 5 là nghiệm của phương trình (1), do đó ta có:

Vậy 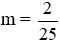là giá trị cần tìm

Ví dụ 3: Cho hàm số y = (m-1)x² có đồ thị là parabol (P). Tìm m biết rằng (P) cắt đường thẳng (d): y = 3 - 2x tại điểm có tung độ bằng 5

Giải

Vì (P) cắt đường thẳng y = 3 - 2x tại điểm có tung độ bằng 5 nên điểm này thuộc đường thẳng (d). Thay y = 5 vào phương trình đường thẳng (d), ta có:

5 = 3 – 2x ⇔ x = -1

Điểm có tọa độ (-1;5) cũng thuộc (P) nên : 5 = (m – 1).(-1)² ⇔5 = m - 1 ⇔ m = 6

Vậy m = 6 là giá trị cần tìm

B. Bài tập

Câu 1: Cho 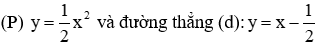. Tìm tọa độ giao điểm của (P) và đường thẳng (d)

Giải

Phương trình hoành độ giao điểm:

Thay x = 1 vào phương trình đường thẳng (d) ta được y =

Vậy (P) cắt đường thẳng (d) tại điểm có tọa độ là

Đáp án đúng là A

Câu 2: Cho (P) y = 3x² và đường thẳng (d): y = -4x - 1. Số giao điểm của (P) và đường thẳng (d)

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình hoành độ giao điểm: 3x² = -4x - 1 ⇔ 3x² + 4x + 1 = 0

Phương trình trên là phương trình bậc hai có a – b + c = 3 – 4 + 1 = 0 nên có hai nghiệm x = -1, x =

Vậy (P) cắt đường thẳng (d) tại 2 điểm

Đáp án đúng là C

Câu 3: Cho (P) 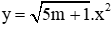và đường thẳng (d): y = 5x + 4. Tìm m để (P) và đường thẳng (d) cắt nhau tại điểm có tung độ bằng 9

A. m = 5

B. m = 15

C. m = 6

D. m = 16

Giải

Điều kiện:

Vì (P) cắt đường thẳng (d) tại điểm có tung độ bằng 9 nên điểm này thuộc đường thẳng (d). Thay y = 9 vào phương trình đường thẳng (d), ta có:

9 = 5x + 4 ⇔ x = 1

Điểm có tọa độ (1;9) cũng thuộc (P) nên:

Đáp án đúng là D

Câu 4: Cho (P) 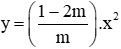và đường thẳng (d): y = 2x + 2. Biết (P) cắt (d) tại điểm có tung độ bằng 4. Tìm hoành độ giao điểm của (P) và (d)

Giải

Vì (P) cắt đường thẳng (d) tại điểm có tung độ bằng 4 nên điểm này thuộc đường thẳng (d). Thay y = 4 vào phương trình đường thẳng (d), ta có:

4 = 2x + 2 ⇔ x = 1

Phương trình hoành độ giao điểm của (P) và (d):

4x² = 2x + 2 ⇔ 4x² - 2x - 2 = 0

Phương trình trên là phương trình bậc hai có a + b + c = 4 – 2 – 2 = 0 nên có 2 nghiệm x = 1, x =

Đáp án đúng là A

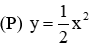
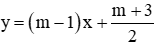
Câu 5: Cho và đường thẳng (d): . Tìm m để (P) và (d) cắt nhau tại 2 điểm phân biệt

A. m > 1

B. m = 1

C. m < -2

D. m ∈ R

Giải

Phương trình hoành độ giao điểm:

(P) và (d) cắt nhau tại 2 điểm phân biệt khi phương trình (1) có 2 nghiệm phân biệt ⇔ Δ' > 0

Đáp án đúng là D

Câu 6: Cho (P) y = x² và đường thẳng (d): y = mx - m. Tìm m để (d) tiếp xúc với (P)

A. m = 1, m = 2

B. m = 0, m = 4

C. m = -1, m = 2

D. m = 2, m = 4

Giải

Phương trình hoành độ giao điểm: x² = mx - m ⇔ x² - mx + m = 0(1)

(d) tiếp xúc với (P) khi phương trình (1) có nghiệm kép ⇔ Δ = 0

Đáp án đúng là B

Câu 7: Cho (P) y = 2x² và đường thẳng (d): y = x - m. Tìm m để (d) và (P) không có điểm chung

Giải

Phương trình hoành độ giao điểm: 2x² = x - m ⇔ 2x² - x + m = 0(1)

(d) và (P) không có điểm chung khi phương trình (1) vô nghiệm

Đáp án đúng là A

Câu 8: Cho (P) y = x² + 1 và đường thẳng (d): y = 2x + 1. Biết (d) và (P) cắt nhau tại 2 điểm phân biệt, tọa độ của 2 điểm đó là

A. (0;-1) và (2;5)

B. (0;1) và (2;5)

C. (1;0) và (2;5)

D. (1;0) và (5;2)

Giải

Phương trình hoành độ giao điểm:

Khi x = 0 thay vào phương trình của (d) ta tính được y = 1

Khi x = 2 thay vào phương trình của (d) ta tính được y = 5

Vậy tọa độ giao điểm của (P) và (d) là: (0;1) và (2;5)

Đáp án đúng là B

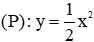
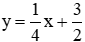
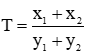
Câu 9: Trong mặt phẳng với hệ tọa độ, cho parabol và đường thẳng . Gọi (x₁;y₁) và B(x₂;y₂) lần lượt là các giao điểm của (P) với (d). Tính giá trị biểu thức .

Giải

Phương trình hoành độ giao điểm của (P) và (d):

Đáp án đúng là D