Lý thuyết Tỉ số lượng giác của góc nhọn hay, chi tiết | Toán lớp 9

Lý thuyết Tỉ số lượng giác của góc nhọn hay, chi tiết

Tài liệu Lý thuyết Tỉ số lượng giác của góc nhọn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Tỉ số lượng giác của góc nhọn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định nghĩa

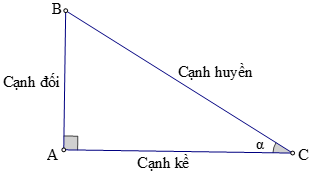
    + Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

    + Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.

    + Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.

    + Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.

Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.

Nhận xét: Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0

2. Tỉ số lượng giác của hai góc phụ nhau

Với hai góc α, β mà α + β = 90°,

Ta có: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.

Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.

3. Một số góc đặc biệt

Với một số góc đặc biệt ta có:

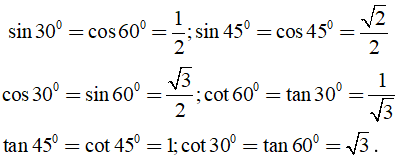
4. Ví dụ cụ thể

Câu 1: Biết sinα = 5/13. Tính cosα, tanα và cotα.

Hướng dẫn:

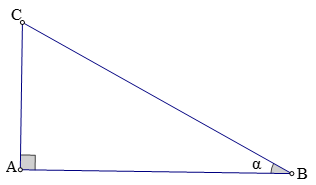
Xét ΔABC vuông tại A.

Câu 2: Biết sinα.cosα = 12/25. Tính sinα, cosα.

Hướng dẫn:

Biết sinα.cosα = 12/25. Để tính sinα,cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα.

Ta có:

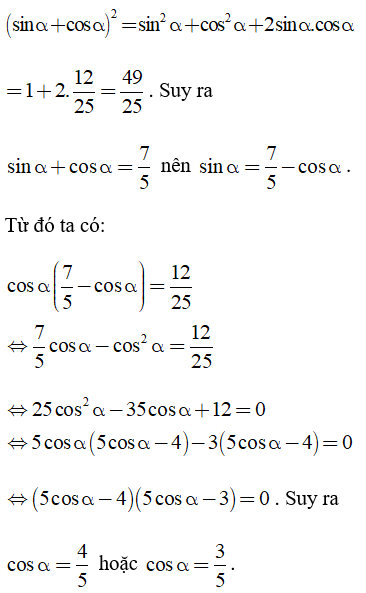
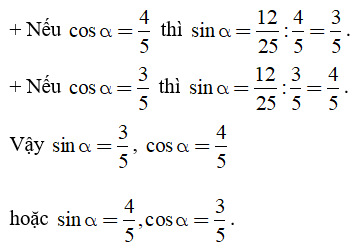
B. Bài tập tự luận

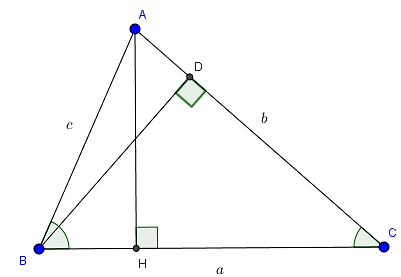
Câu 1: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .

Lời giải:

Câu 2: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: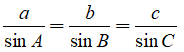

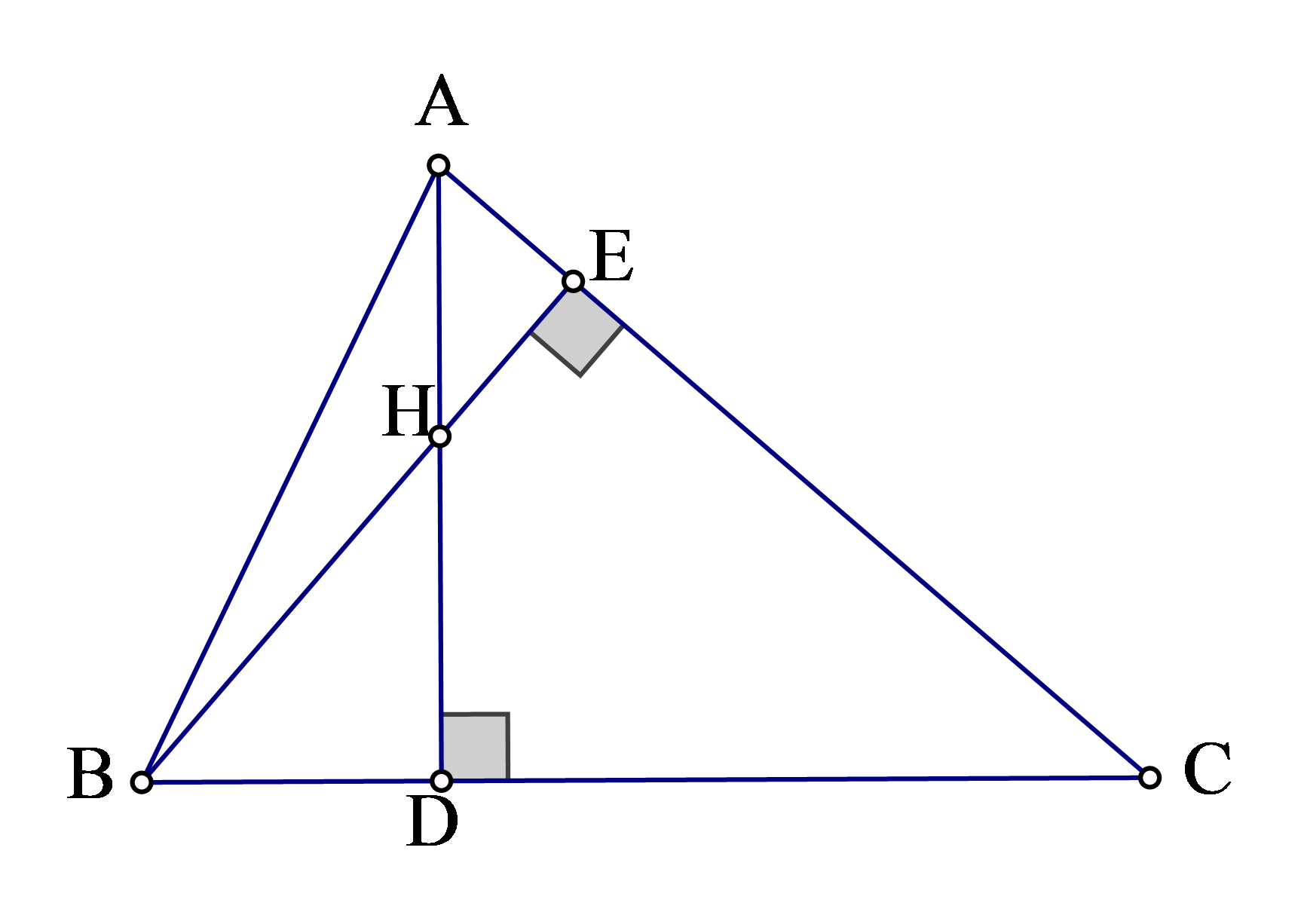
Lời giải: