Lý thuyết Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết | Toán lớp 9
Lý thuyết Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết
Tài liệu Lý thuyết Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Vị trí tương đối của đường thẳng và đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Ba vị trí tương đối của đường thẳng và đường tròn
a) Đường thẳng và đường tròn cắt nhau
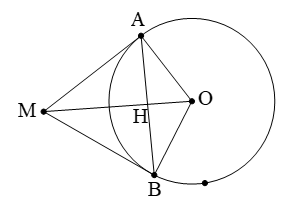
Khi một đường thẳng có hai điểm chung A, B với đường tròn (O) ta nói đường thẳng cắt đường tròn tại hai điểm phân biệt. Khi đó ta có những kết quả quan trọng sau:
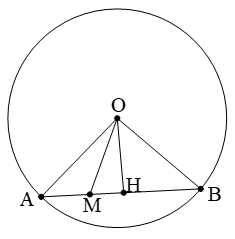
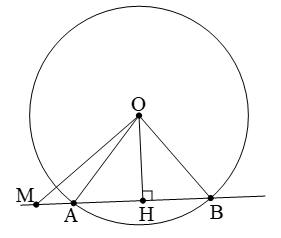
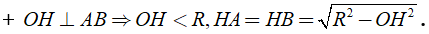
Theo định lý Pitago ta có: OH2 = MO2 - MH2
Mặt khác ta cũng có: OH2 = R2 - AH2 nên suy ra
MO2 - MH2 = R2 - AH2 ⇔ MH2 - AH2 = MO2 - R2
⇔ (MH - AH)(MH + AH) = MO2 - R2
+ Nếu M nằm ngoài đoạn AB thì MA.MB = MO2 - R2
+ Nếu M nằm trong đoạn AB thì MA.MB = R2 - MO2
Mối liên hệ khoảng cách và dây cung: R2 = OH2 + AB2/4
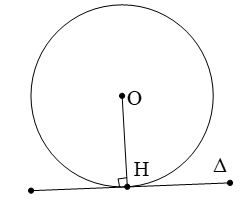
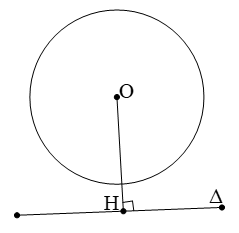
b) Đường thẳng và đường tròn tiếp xúc nhau.
Khi một đường thẳng Δ chỉ có một điểm chung H với đường tròn (O), ta nói đường thẳng tiếp xúc với đường tròn, hay Δ là tiếp tuyến của đường tròn (O). Điểm H gọi là tiếp điểm của tiếp tuyến với đường tròn (O)
Như vậy nếu Δ là tiếp tuyến của (O) thì Δ vuông góc với bán kính đi qua tiếp điểm
Ta có OH = R

c) Đường thẳng và đường tròn không giao nhau
Khi một đường thẳng Δ và đường tròn (O) không có điểm chung ta nói đường thẳng Δ và đường tròn (O) không giao nhau. Khi đó OH > R
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau | 2 | d < R |
| Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
| Đường thẳng và đường tròn không giao nhau | 0 | d > R |
3. Ví dụ cụ thể
Câu 1: Cho đường tròn tâm O bán kính bằng 6cm và một điểm A cách O 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài đoạn AB.
Hướng dẫn:
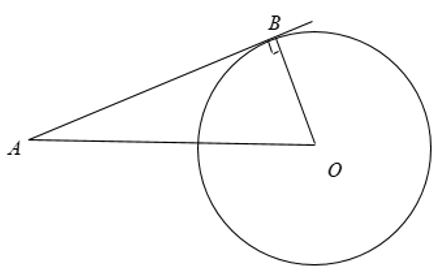
OA = 10cm ⇒ A nằm ngoài đường tròn
Ta có: AB là tiếp tuyến, B là tiếp điểm, khi đó OB = R = 6cm.
AB ⊥ OB áp dụng định lý Py – ta – go ta có:
AB2 + OB2 = OA2
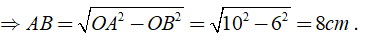
Vậy AB = 8cm

B. Bài tập tự luận
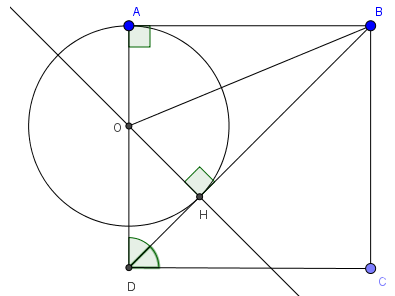
Câu 1: Cho hình vuông ABCD. Trên đường chéo BD lấy điểm H sao cho BH = BA , qua H vẽ đường thẳng vuông góc với BD cắt AD tại O
a) So sánh OA, OH và HD
b) Xác định vị trí tương đối của BD với (O; OA)
Lời giải:

Câu 2: Cho đường tròn (O; 5) . Từ M ngoài O vẽ hai tiếp tuyến MA, MB sao cho MA ⊥ MB tại M.
a) Tính MA, MB
b) Gọi I là giao điểm của OM với (O) . Kẻ tiếp tuyến với (O) tại I cắt OA, OB lần lượt ở C và D. Tính CD
Lời giải:
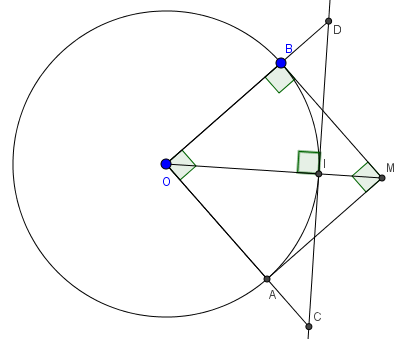
a) Ta có: MA, MB là hai tiếp tuyến nên khoảng cách từ O đến MA và MB lần lượt là OA và OB (do A, B là các tiếp điểm duy nhất với (O))
Từ đó ta có: OA ⊥ MA, OB ⊥ MB
Tứ giác OAMB có 3 góc vuông và OA = OB = R nên OAMB là hình vuông
⇒ MA = MB = R = 5
b) Dễ dàng chứng minh


