Bài tập Đường tròn cực hay, chọn lọc, có lời giải chi tiết | Toán lớp 9
Bài tập Đường tròn cực hay, chọn lọc, có lời giải chi tiết
Với Bài tập Đường tròn cực hay, chọn lọc, có lời giải chi tiết Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Bài 1: Đường tròn là hình:
A. Không có trục đối xứng
B. Có một trục đối xứng
C. Có hai trục đối xứng
D. Có vô số trục đối xứng
Bài 2: Cho (O; 15cm) có dây AB = 24 cm thì khoảng cách từ tâm O đến dây AB là:
A. 12 cm B. 9 cm C. 8 cm D. 6 cm
Bài 3: Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp tam giác là điểm nằm ở:
A. Ngoài tam giác
B. Trong tam giác
C. Là trung điểm của cạnh nhỏ nhất
D. Là trung điểm của cạnh lớn nhất
Bài 4: Cho đoạn thẳng OI = 8 cm. Vẽ các đường tròn (O; 10cm); (I; 2cm). Hai đường tròn (O) và (I) có vị trí tương đối như thế nào với nhau?
A. (O) và (I) cắt nhau
B. (O) và (I) tiếp xúc ngoài với nhau
C. (O) và (I) tiếp xúc trong với nhau
D. (O) và (I) không cắt nhau
Bài 5: Cho (O; 6cm) và đường thẳng a. Gọi d là khoảng cách từ tâm O đến a. Điều kiện để a cắt (O) là:
A. Khoảng cách d < 6cm
B. Khoảng cách d = 6 cm
C. Khoảng cách d ≤ 6cm
D. Khoảng cách d > 6 cm
Bài 6: Tâm đường tròn ngoại tiếp tam giác là:
A. Giao của 3 đường trung tuyến
B. Giao của 3 đường phân giác
C. Giao của 3 đường trung trực
D. Giao của 3 đường cao
Bài 7: Gọi d là khoảng cách hai tâm của hai đường tròn (O, R) và (O', r) (với 0 < r < R). Để (O) và (O') ở ngoài nhau thì
A. d < R – r B. d = R – r
C. d = R + r D. d > R + r
Bài 8: Cho tam giác ABC có độ dài các cạnh AB = 7 cm; AC = 24 cm; BC = 25 cm. Bán kính đường tròn ngoại tiếp tam giác ABC là:
A. 10 cm B. 12,5 cm C. 12 cm D. Một số khác
Bài 9: Cho AB và AC là 2 tiếp tuyến của (O) với B, C là các tiếp điểm. Câu trả lời nào sau đây là sai?
A. AB = AC B. AB = BC
C. AO là trục đối xứng của dây BC
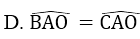
Bài 10: Cho hai đường tròn (O;5) và (O’;5) cắt nhau tại A và B. Biết OO’=8. Độ dài dây cung chung AB là:
A. 4 C. 6
B. 5 D.7

Bài 11: Cho đường tròn (O;R) đường kính AB. M là một điểm nằm giữa A và B. Qua M vẽ dây CD vuông góc với AB
Biết AM = 4, R = 6,5. Giá trị diện tích tam giác BCD là bao nhiêu?
A. 50 C. 54
B. 52 D. 56
Bài 12: Cho 2 đường tròn (O;R) và (O’;r), R > r
Trong các phát biểu sau phát biểu nào là phát biểu sai
A. Hai đường tròn (O) và (O’) cắt nhau khi và chỉ khi R - r < OO' < R + r
B. Hai đường tròn (O) và (O’) tiếp xúc ngoài khi và chỉ khi OO’ = R - r
C. Hai đường tròn (O) và (O’) tiếp xúc trong khi và chỉ khi OO’ = R - r
D. Hai đường tròn (O) và (O’) gọi là ngoài nhau khi và chỉ khi OO’ > R + r
Bài 13: Cho đường thẳng d. Tâm các đường tròn có bán kính là 2 và tiếp xúc với d nằm trên đường nào
A. Một đường thẳng song song với d và cách d một khoảng là 1
B. Một đường thẳng song song với d và cách d một khoảng là 2
C. Hai đường thẳng song song với d và cách d một khoảng là 4
D. Hai đường thẳng song song với d và cách d một khoảng là 2
Bài 14: Cho (O; 5cm) và đường thẳng d. Gọi OH là khoảng cách từ tâm O đến a. Điều kiện để a và O có 2 điểm chung là:
A. Khoảng cách OH ≤ 5 cm
B. Khoảng cách OH = 5 cm
C. Khoảng cách OH > 5 cm
D. Khoảng cách OH < 5 cm
Bài 15: Cho tam giác ABC có độ dài các cạnh AB = 12 cm; AC = 16 cm; BC = 20 cm. Bán kính đường tròn ngoại tiếp tam giác ABC là:
A. 6 cm B. 8 cm C. 10 cm D. 12 cm
Bài 16: Cho (O, 15 cm), dây AB cách tâm 9 cm thì độ dài dây AB là:
A. 12 cm B. 16 cm C. 20 cm D. 24 cm
Bài 17: Cho AB, AC là 2 tiếp tuyến của đường tròn (O) với B, C là các tiếp điểm thì câu nào sau đây là đúng?
A. AB = BC
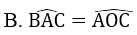
C. AO ⊥ BC
D. BO = AC
Bài 18: Gọi d là khoảng cách 2 tâm của (O, R) và (O', r) với 0 < r < R. Để (O) và (O') tiếp xúc trong thì:
A. R - r < d < R + r B. d = R - r
C. d > R + r D. d = R + r
Bài 19: Cho đường tròn (O; 25). Khi đó dây lớn nhất của đường tròn (O; 25) có độ dài là:
A. 12,5 C. 50
B. 25 D. 20
Bài 20: Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
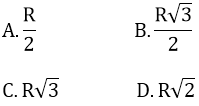

Đáp án và hướng dẫn giải
| 1. D | 2. B | 3. A | 4. C | 5. A |
| 6. C | 7. D | 8. B | 9. B | 10. C |
| 11. C | 12. B | 13. B | 14. D | 15. C |
| 16. D | 17. C | 18. B | 19. B | 20. C |
Bài 11:
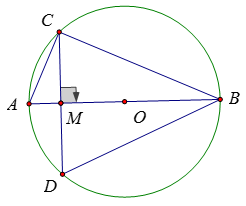
ΔABC vuông tại C có CM là đường cao
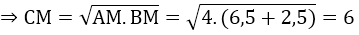
⇒ CD = 2CM = 12
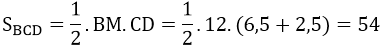
Chọn đáp án C
Bài 20:
Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
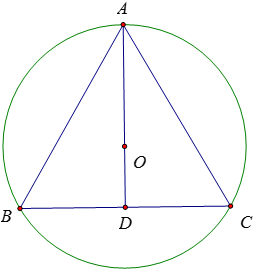
Gọi D là trung điểm của BC
ΔABC đều cạnh a nên
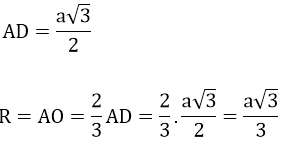
⇒ a = R√3
Chọn đáp án C
Bài 21:
ΔOAB vuông tại O có OM là trung tuyến nên
OM = AB/2 = 4
Điểm M luôn cách điểm O một khoảng cố định là 4. Vậy tập hợp điểm M là đường tròn tâm O, bán kính 4.
Chọn đáp án C
Bài 22:
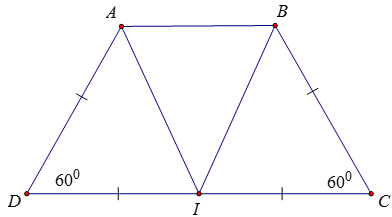
Hình thang ABCD có 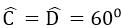
⇒ AD = BC
Gọi I là trung điểm của DC ⇒ AD = DI = IC = BC = 4
ΔADI cân có góc D bằng 600 nên ΔADI đều ⇒ AI = DI
Tương tự: BI = CI
Vậy 4 điểm A, B, C, D thuộc đường tròn (I; 4)
Chọn đáp án D
Bài 23:
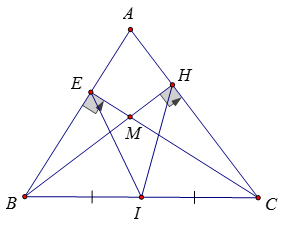
góc BEC bằng 900 nên E thuộc đường tròn đường kính BC
góc BHC ̂bằng 900 nên H thuộc đường tròn đường kính BC
Vậy B, C, E, H cùng thuộc đường tròn tâm I, bán kính IB
Chọn đáp án B
Bài 25:
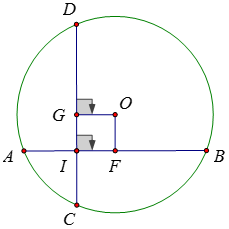
Gọi F, G lần lượt là hình chiếu của O lên AB và CD
Tứ giác OGIF có 3 góc vuông nên là hình chữ nhật
Lại có OG = OF (do AB = CD) nên OGIF là hình vuông
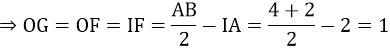
Vậy d = d’ = 1
Bài 26:
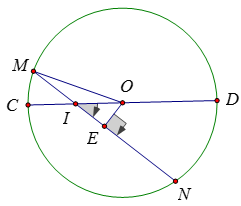
Kẻ OE ⊥ MN ⇒ E là trung điểm của MN
OE = OI.sin300 = 6.sin300 = 3
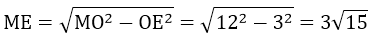
⇒ MN = 2ME = 6√15
Bài 27:
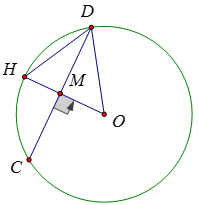
Ta có: OM2 = OD2 - DM2
⇒ (R - 4)2 = R2 - 82 ⇒ R = 10
Bài 30:
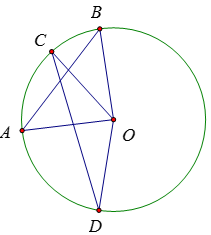
Các ΔOAB và ΔOCD cân tại O nên
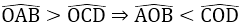
⇒ AB < CD
Bài 37:
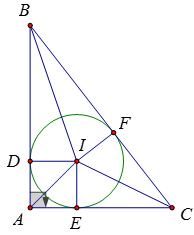
Tam giác ABC vuông tại A có AB = 3, AC = 4 ⇒ BC = 5
Ta có: CE = CF; BF = BD; AD = AE
⇒ 2AD = AB + AC = BC = 2 ⇒ AD = 1
Tứ giác ADIE có 3 góc vuông, ID = IE nên ADIE là hình vuông
⇒ r = ID = AD = 1
Bài 39:
Ta có:
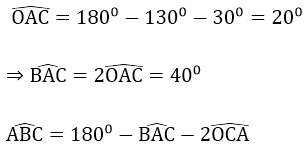
= 1800 - 400 - 600 = 800
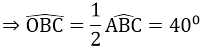
Xét tam giác OBC có:
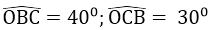
⇒ OB < OC

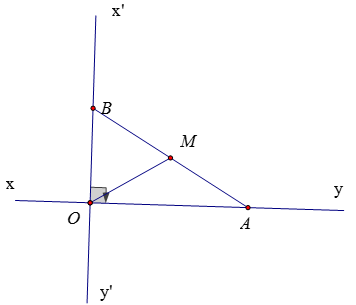
Bài 21: Cho hai đường thẳng xy và x’y’ vuông góc với nhau tại O. Một đoạn thẳng AB = 8 chuyển động sao cho A luôn nằm trên xy và B luôn nằm trên x’y’. Khi đó trung điểm M của đoạn AB di chuyển trên đoạn nào?
A. Đường thẳng song song với xy cách xy một đoạn là 4
B. Đường thẳng song song với x’y’ cách x’y’ một đoạn là 4
C. Đường tròn tâm O bán kính là 4
D. Đường tròn tâm O bán kính là 8
Bài 22: Cho hình thang ABCD (AB // CD), 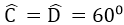
A. (I, R = 4√2) với I là trung điểm của CD
B. (O, R = 4√2) với O là giao điểm của AC và BD
C. (O, R = 4) với O là giao điểm của AC và BD
D. (I, R = 4) với I là trung điểm của CD
Bài 23: Cho tam giác ABC có BH, CE là các đường cao. Gọi M là giao điểm BH và CE. I là trung điểm BC. Khi đó B, C, E, H cùng thuộc đường tròn nào?
A. (I; R = IA)
B. (I; R = IB)
C. (M; R = MB)
D. (M; R = MA)
Bài 24: Cho đường tròn tâm A đường kính BC. Gọi D là trung điểm AB. Dây EF vuông góc với AB tại D. Tứ giác EBFA là hình gì?
A. Hình chữ nhật
B. Hình vuông
C. Hình thoi
D. Chưa đủ dữ kiện để kết luận
Bài 25: Cho đường tròn (O; R) và 2 dây AB và CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2, IB = 4. Khoảng cách từ tâm O tới AB là d và tới CD là d’
Giá trị của d và d’
A. d = 2; d′ = 1
B. d = d′ = 1
C. d = d′ = 2
D. d = 1; d′ = 2
Bài 26: Cho đường tròn (O; 12) có đường kính CD. Dây MN qua trung điểm I của OC sao cho góc NID bằng 30 độ. MN = ?
A. 6√15 C. 9
B. 6√2 D. 6
Bài 27: Cho đường tròn (O; R) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O) tại H. Biết CD = 16, MH = 4.R = ?
A. 8 C. 10
B. 9 D. 11
Bài 28: Cho (O; 25), dây AB = 40. Vẽ dây CD song song với AB và có khoảng cách tới AB là 22. Độ dài dây CD là?
A. 42 C. 46
B. 44 D. 48
Bài 29: Cho đường tròn (O; 25) và hai dây MN // PQ có độ dài theo thứ tự là 40 và 48. Khi đó khoảng cách giữa MN và PQ là:
A. 22 C. 30
B. 8 D. 22 hoặc 8
Bài 30: Cho đường tròn (O; R) 2 dây cung AB và CD. Biết rằng: 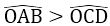
A. AB > CD
B. AB = CD
C. AB < CD
D. Chưa đủ dữ kiện để kết luận

Bài 31: Câu nào trong các câu sau đây là câu đúng:
A. Đường thẳng tiếp xúc với đường tròn khi đường thẳng đó có 2 giao điểm với đường tròn
B. Đường thẳng cắt đường tròn khi đường thẳng đó có 1 giao điểm với đường tròn
C. Đường thẳng không giao nhau với đường tròn khi nó chỉ có 1 giao điểm với đường tròn
D. Đường thẳng cắt đường tròn khi đường thẳng đó có 2 giao điểm với đường tròn
Bài 32: Cho tam giác ABC có AH là đường cao (H thuộc BC). Đường tròn (A; AH) sẽ có vị trí như thế nào với các cạnh của tam giác ABC
A. (A; AH) tiếp xúc với AB,AC và cắt BC
B. (A; AH) tiếp xúc với BC, AC và không cắt AB
C. (A; AH) cắt AB, AC và tiếp xúc với BC
D. (A; AH) cắt AB và tiếp xúc với BC, AC
Bài 33: Trong các phát biếu dưới đây phát biểu nào đúng:
A. Đường thẳng d được gọi là tiếp tuyến của (O) khi chúng có điểm chung
B. Đường thẳng d được gọi là tiếp tuyến khi d vuông góc với bán kính OA và OA < R
C. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính OA và A thuộc đường tròn
D. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với OA tại A và OA > R
Bài 34: Cho đường tròn (O). A, B, C là 3 điểm thuộc đường tròn sao cho tam giác ABC cân tại A. Phát biểu nào sau đây đúng
Tiếp tuyến của đường tròn tại A là
A. Đi qua A và vuông góc AB
B. Đi qua A và song song BC
C. Đi qua A và song song AC
D. Đi qua A và vuông góc BC
Bài 35: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó:
A. AC là tiếp tuyến của (B; 3)
B. AB là tiếp tuyến của (C; 3)
C. AB là tiếp tuyến của (B; 4)
D. AC là tiếp tuyến của (C; 4)
Bài 36: Phát biểu nào sau đây là đúng
A. Có 3 đường tròn nội tiếp một tam giác
B. Có chỉ một đường tròn bàng tiếp một tam giác
C. Giao điểm của các đường phân giác trong chính là tâm đường tròn bàng tiếp tam giác đó
D. Giao điểm của phân giác trong góc A và phân giác ngoài tại B là tâm đường tròn bầng tiếp trong góc A
Bài 37: Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Đường tròn (I; r) nội tiếp tam giác ABC. Giá trị của r là:
A. 1 C.3
B. 2 D.4
Bài 38: Cho tam giác ACB vuông tại A. O là tâm đường tròn nội tiếp tam giác ABC. D, E, F lần lượt là các tiếp điểm trên AB, AC, BC. Hệ thức nào đúng
A. AD = AC + AB - BC
B. 2AD = AB + AC - BC
C. 2EC = AB + AC - BC
D. 2BD = AC + BC - AB
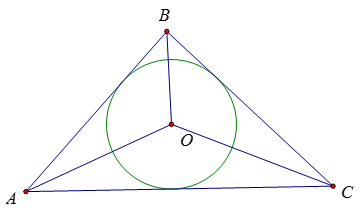
Bài 39: Cho tam giác ABC ngoại tiếp đường tròn (O). Biết góc AOC bằng 1300, góc OCA bằng 300. So sánh OB và OC
A. OB < OC
B. OB > OC
C. OB = OC
D. Chưa đủ dữ kiện để so sánh
Bài 40: Cho đường tròn (O; 10) và (O’; 3). Biết OO’ = 8. Vị trí tương đối của hai đường tròn là
A. (O) chứa (O’) C. Tiếp xúc trong
B. Cắt nhau D. Tiếp xúc ngoài

Đáp án và hướng dẫn giải
| 21. C | 22. D | 23. B | 24. C | 25. B |
| 26. A | 27. C | 28. D | 29. D | 30. C |
| 31. D | 32. C | 33. C | 34. B | 35. A |
| 36. D | 37. A | 38. B | 39. A | 40. B |
Bài 21:

ΔOAB vuông tại O có OM là trung tuyến nên
OM = AB/2 = 4
Điểm M luôn cách điểm O một khoảng cố định là 4. Vậy tập hợp điểm M là đường tròn tâm O, bán kính 4.
Chọn đáp án C
Bài 22:

Hình thang ABCD có 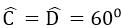
⇒ AD = BC
Gọi I là trung điểm của DC ⇒ AD = DI = IC = BC = 4
ΔADI cân có góc D bằng 600 nên ΔADI đều ⇒ AI = DI
Tương tự: BI = CI
Vậy 4 điểm A, B, C, D thuộc đường tròn (I; 4)
Chọn đáp án D
Bài 23:

góc BEC bằng 900 nên E thuộc đường tròn đường kính BC
góc BHC ̂bằng 900 nên H thuộc đường tròn đường kính BC
Vậy B, C, E, H cùng thuộc đường tròn tâm I, bán kính IB
Chọn đáp án B
Bài 25:

Gọi F, G lần lượt là hình chiếu của O lên AB và CD
Tứ giác OGIF có 3 góc vuông nên là hình chữ nhật
Lại có OG = OF (do AB = CD) nên OGIF là hình vuông
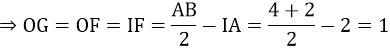
Vậy d = d’ = 1

Bài 26:

Kẻ OE ⊥ MN ⇒ E là trung điểm của MN
OE = OI.sin300 = 6.sin300 = 3
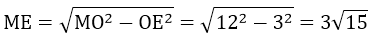
⇒ MN = 2ME = 6√15
Bài 27:

Ta có: OM2 = OD2 - DM2
⇒ (R - 4)2 = R2 - 82 ⇒ R = 10
Bài 30:

Các ΔOAB và ΔOCD cân tại O nên
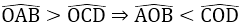
⇒ AB < CD
Bài 37:

Tam giác ABC vuông tại A có AB = 3, AC = 4 ⇒ BC = 5
Ta có: CE = CF; BF = BD; AD = AE
⇒ 2AD = AB + AC = BC = 2 ⇒ AD = 1
Tứ giác ADIE có 3 góc vuông, ID = IE nên ADIE là hình vuông
⇒ r = ID = AD = 1
Bài 39:

Ta có:
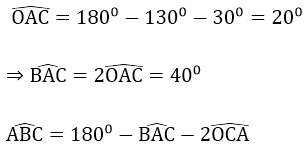
= 1800 - 400 - 600 = 800
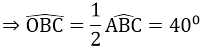
Xét tam giác OBC có:
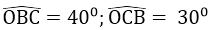
⇒ OB < OC

