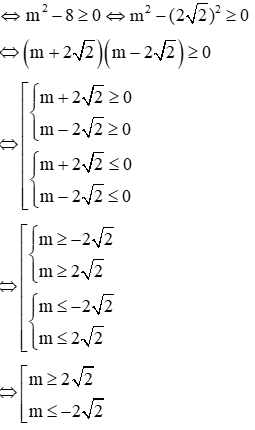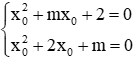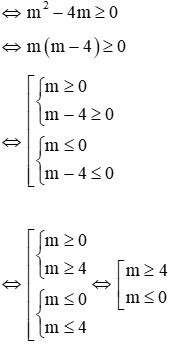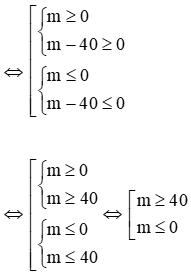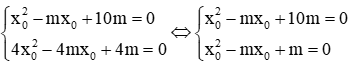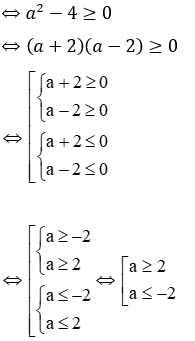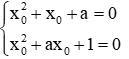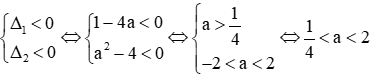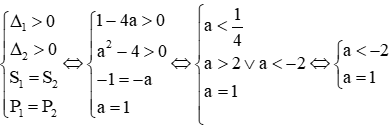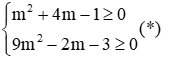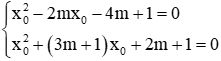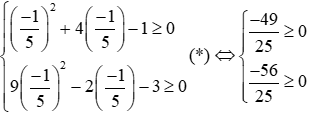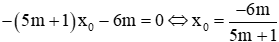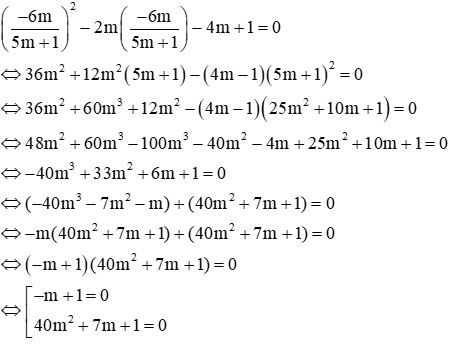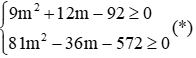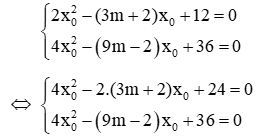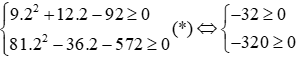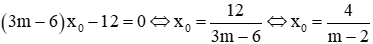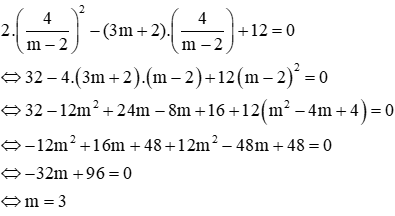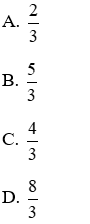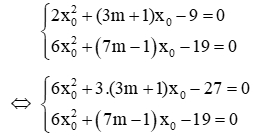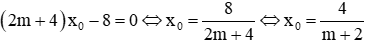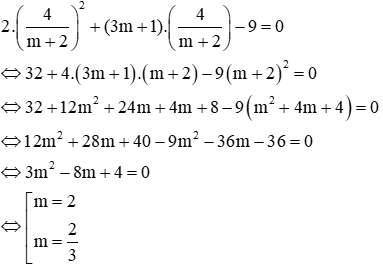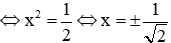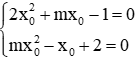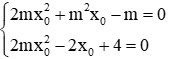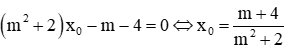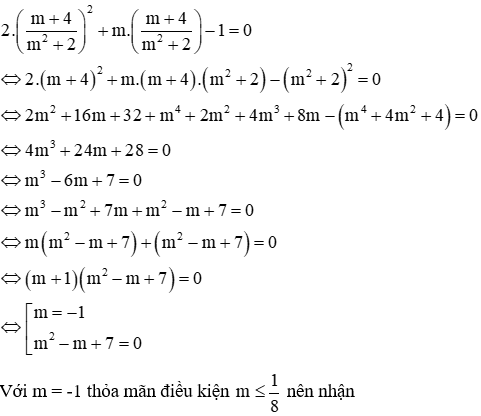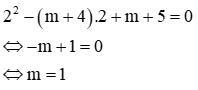Cách tìm m để hai phương trình có nghiệm chung cực hay | Toán lớp 9

Cách tìm m để hai phương trình có nghiệm chung cực hay

Với Cách tìm m để hai phương trình có nghiệm chung cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm m để hai phương trình có nghiệm chung từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

- Bài toán: Cho 2 phương trình dạng ax² + bx + c = 0 có chứa tham số m. Tìm m để 2 phương trình có ít nhất một nghiệm chung

- Cách giải:

+ B1: Tìm điều kiện của m để 2 phương trình cùng có nghiệm

+ B2: Giả sử x₀ là nghiệm chung của 2 phương trình. Tìm x₀

+ B3: Thế x₀ tìm được vào một trong hai phương trình tìm m

+ B4: Đối chiếu m tìm được với điều kiện ở B₁, nếu thỏa mãn thì nhận, không thỏa mãn thì loại

Ví dụ 1: Cho 2 phương trình : x² + mx + 2 = 0(1) và x² + 2x + m = 0(2). Tìm m để hai phương trình có ít nhất một nghiệm chung

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0

Phương trình (2 ) có nghiệm khi: Δ' ≥ 0 ⇔ 1 - m ≥ 0 ⇔ m ≤ 1

⇒ Điều kiện để 2 phương trình cùng có nghiệm là m ≤ -2√2 (*)

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: mx₀ - 2x₀ + 2 - m = 0 ⇔ (m - 2)x₀ = m - 2

Do m ≤ -2√2 nên m – 2 ≠ 0, suy ra x₀ = 1

Thay x₀ = 1 vào phương trình (1): 1 + m + 2 = 0 hay m = -3( thỏa mãn (*))

Vậy với m = -3 thì 2 phương trình có ít nhất một nghiệm chung

Ví dụ 2: Cho 2 phương trình : x² - 2mx + 4m = 0(1) và x² - mx + 10m = 0(2) . Tìm m để phương trình (2) có một nghiệm gấp 2 lần một nghiệm của phương trình (1)

Giải

Phương trình (1) có nghiệm khi: Δ' ≥ 0

Phương trình (2 ) có nghiệm khi: Δ ≥ 0

⇔ m² - 40m ≥ 0 ⇔ m(m - 40) ≥ 0

⇒ Điều kiện để 2 phương trình cùng có nghiệm là m ≥ 40 ∨ m ≤ 0 (*)

Giả sử x₀ là nghiệm của phương trình (2) thì 2x₀ là nghiệm của phương trình (1). Thay x₀ vào (2) và 2x₀ vào (1) ta có:

Trừ 2 phương trình cho nhau ta được: 9m = 0 ⇔ m = 0 (thỏa mãn (*))

Vậy với m = 0 thì phương trình (2) có một nghiệm gấp 2 lần một nghiệm của phương trình (1)

Ví dụ 3: Cho 2 phương trình : x² + x + a = 0(1) và x² + ax + 1 = 0(2).

a. Tìm a để 2 phương trình có ít nhất một nghiệm chung

b. Tìm a để 2 phương trình tương đương

Giải

a. Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ 1 – 4a ≥ 0 ⇔ a ≤ 1/4

Phương trình (2 ) có nghiệm khi: Δ ≥ 0

Điều kiện để 2 phương trình cùng có nghiệm là: a ≤ -2 (*)

Giả sử x₀ là nghiệm chung của 2 phương trình (2) ta có:

Trừ 2 phương trình cho nhau ta được: x₀(1 – a) – (1 – a) = 0

⇔ x₀(1 – a) = (1 – a) (**)

Vì a ≤ -2 nên 1 – a luôn khác 0. Chia hai vế của (**) cho 1 – a ta được x₀ = 1

Thay x₀ = 1 vào (1) ta có: a = -2 ( thỏa mãn (*))

Vậy với a = -2 thì 2 phương trình có ít nhất một nghiệm chung

b. Kí hiệu ∆₁, S₁, P₁ lần lượt là biệt thức đen-ta, tổng 2 nghiệm, tích 2 nghiệm của phương trình (1)

Kí hiệu ∆₂, S₂, P₂ lần lượt là biệt thức đen-ta, tổng 2 nghiệm, tích 2 nghiệm l của phương trình (2)

Hai phương trình tương đương khi chúng có cùng tập nghiệm . Ta xét các trường hợp sau:

+ TH₁: Hai phương trình cùng có tập nghiệm là rỗng

Trường hợp này xảy ra khi:

+ TH₂: Hai phương trình có nghiệm kép giống nhau

Trường hợp này xảy ra khi 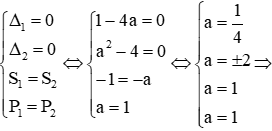vô nghiệm

+ TH₃: Hai phương trình có nghiệm phân biệt giống nhau

Trường hợp này xảy ra khi

⇒ vô nghiệm

Vậy với 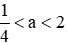thì 2 phương trình đã cho tương đương

B. Bài tập

Câu 1: Số giá trị của m để hai phương trình x² – 2mx – 4m + 1 = 0 (1) và x² + (3m + 1)x + 2m + 1 = 0 (2) có nghiệm chung là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có nghiệm khi Δ' ≥ 0 ⇔ m² + 4m - 1 ≥ 0

Phương trình (2 ) có nghiệm khi Δ ≥ 0 ⇔ (3m + 1)² - 4(2m + 1) ≥ 0 ⇔ 9m² - 2m - 3 ≥ 0

Điều kiện để hai phương trình có nghiệm là:

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: -2mx₀ - (3m + 1)x₀ - 4m + 1 - 2m - 1 = 0 ⇔ -(5m + 1)x₀ - 6m = 0

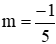
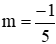
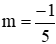
Nếu thì 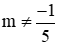điều kiện (*) trở thành

⇒ không thỏa mãn (*), nghĩa là với thì hai phương trình đều vô nghiệm. Vậy muốn hai phương trình có nghiệm chung thì

Khi thì

Thay vào phương trình (1):

Xét –m + 1 = 0 ⇔ m = 1( thỏa mãn (*)) ⇒ nhận

Xét 40m² + 7m + 1 = 0 có ∆ = 7² -4.40.1 = -111 < 0 nên vô nghiệm

Vậy với m = 1 thì 2 phương trình có nghiệm chung

Đáp án B

Câu 2: Số giá trị của m để hai phương trình 2x² – (3m + 2)x + 12 = 0 (1) và 4x² - (9m - 2)x + 36 = 0 (2) có nghiệm chung là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (3m + 2)² - 4.2.12 ≥ 0 ⇔ 9m² + 12m - 92 ≥ 0

Phương trình (2) có nghiệm khi: Δ ≥ 0 ⇔ (9m - 2)² - 4.4.36 ≥ 0 ⇔ 81m² - 36m + 4 - 576 ≥ 0 ⇔ 81m² - 36m - 572 ≥ 0

Điều kiện để hai phương trình có nghiệm là:

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: -(6m + 4)x₀ + (9m - 2)x₀ - 12 = 0 ⇔ (3m - 6)x₀ - 12 = 0

Nếu m = 2 thì điều kiện (*) trở thành:

⇒ m = 2 không thỏa mãn (*), nghĩa là với m = 2 thì 2 phương trình cùng vô nghiệm

Vậy muốn hai phương trình có nghiệm chung thì m ≠ 2

Khi m ≠ 2 thì

Thay vào phương trình (1):

Xét m = 3( thỏa mãn (*)) ⇒ nhận

Vậy với m = 3 thì 2 phương trình có nghiệm chung

Đáp án B

Câu 3: Tổng các giá trị của m để hai phương trình 2x² + (3m + 1)x - 9 = 0 (1) và 6x² + (7m - 1)x - 19 = 0 (2) có nghiệm chung là

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (3m + 1)² - 4.2.(-9) ≥ 0 ⇔ (3m + 1)² + 72 ≥ 0,(∀ m ∈ R)

Phương trình (2) có nghiệm khi: Δ ≥ 0 ⇔ (7m - 1)² - 4.6.(-19) ≥ 0 ⇔ (7m-1)² + 456 ≥ 0,(∀ m ∈ R)

⇒ Với mọi m hai phương trình luôn có nghiệm

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: (9m + 3)x₀-(7m-1)x₀-27+19=0 ⇔ (2m + 4)x₀-8=0(*)

Nếu m = -2 thì phương trình (*) vô nghiệm

Nghĩa là với m = -2 thì 2 phương trình cùng không có nghiệm chung

Vậy muốn hai phương trình có nghiệm chung thì m ≠ -2

Khi m ≠ -2 thì

Thay vào phương trình (1):

Vậy với m = 2, 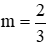thì 2 phương trình có nghiệm chung

Đáp án D

Câu 4: Tích các giá trị của m để hai phương trình 2x² + mx - 1 = 0 (1) và mx² - x + 2 = 0 (2) có nghiệm chung là

A. -1

B. 5

C. 8

D. -10

Giải

+) TH1: m = 0 thì phương trình (1): 2x² - 1 = 0

Phương trình (2): -x + 2 = 0 ⇔ x = 2

⇒ với m = 0 thì hai phương trình không có nghiệm chung

+) TH2: m ≠ 0 thì hai phương trình đều là phương trình bậc hai. Khi đó

Phương trình (1) có nghiệm khi Δ ≥ 0 m² + 8 ≥ 0,(∀ m ∈ R)

Phương trình (2 ) có nghiệm khi Δ ≥ 0 ⇔ 1 - 8m ≥ 0 ⇔ m ≤ 1/8

⇒ Với 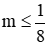hai phương trình luôn có nghiệm

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Vì m ≠ 0 nên ta nhân 2 vế của phương trình thứ nhất với m, nhân 2 vế của phương trình thứ hai với 2 ta được:

Trừ 2 phương trình cho nhau ta được:

Thay vào phương trình (1):

Xét phương trình m² – m + 7 = 0 có ∆ = (-1)² – 4.1.7 = -27 < 0 nên vô nghiệm

Vậy với m = -1 thì 2 phương trình có nghiệm chung

Đáp án A

Câu 5: Cho hai phương trình x² – (m + 4)x + m + 5 = 0 (1) và x² – (m + 2)x + m + 1 = 0 (2), khẳng định nào sau đây là đúng

A. Có một giá trị của m để hai phương trình có nghiệm chung

B. Tích các giá trị của m để hai phương trình có nghiệm chung bằng 10

C. Giá trị của m để hai phương trình có nghiệm chung là số lớn hơn 3

D. Không có giá trị của m để hai phương trình có nghiệm chung

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (m + 4)² - 4(m + 5) ≥ 0

⇔ m² + 8m + 16 - 4m - 20 ≥ 0 ⇔ m² + 4m - 4 ≥ 0

Phương trình (2 ) có nghiệm khi: Δ ≥ 0 ⇔ (m + 2)² - 4(m + 1) ≥ 0

⇔ m² + 4m + 4-4m - 4 ≥ 0 ⇔ m² ≥ 0,(∀ m ∈ R)

⇒ Điều kiện để hai phương trình luôn có nghiệm là: m² + 4m – 4 ≥ 0(*)

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: -(m + 4)x₀ + (m + 2)x₀ + 4 = 0 ⇔ -2x₀ + 4 = 0 ⇔ x₀ = 2

Thay vào phương trình (1):

Với m = 1 thì m² + 4m – 4 = 1 + 4 – 4 = 1 > 0 thỏa mãn điều kiện (*)nên nhận

Vậy với m = 1 thì 2 phương trình có nghiệm chung

Đáp án A