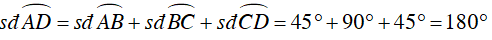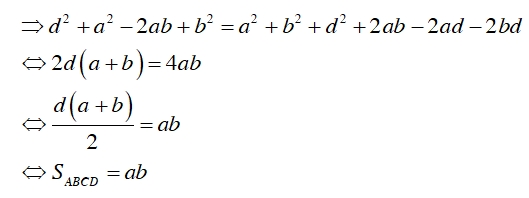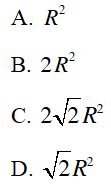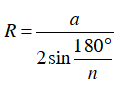Tính các đại lượng liên quan đến đa giác ngoại tiếp, nội tiếp đường tròn | Toán lớp 9
Tính các đại lượng liên quan đến đa giác ngoại tiếp, nội tiếp đường tròn
Với Tính các đại lượng liên quan đến đa giác ngoại tiếp, nội tiếp đường tròn Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính các đại lượng liên quan đến đa giác ngoại tiếp, nội tiếp đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
A. Phương pháp giải
+ Đa giác ngoại tiếp đường tròn là
Nắm vững các kiến thức liên quan đến đa giác nội tiếp, đa giác ngoại tiếp đường tròn.
+ Các công thức tính diện tích tam giác, hình thang, hình chữ nhật, hình vuông,…
B. Ví dụ minh họa
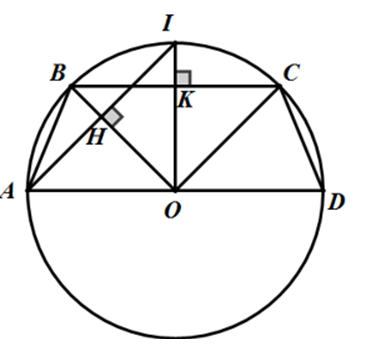
Ví dụ 1 : Trên đường tròn (O; R) lần lượt đặt theo cùng một chiều kẻ từ điểm A, cung AB = 45o , cung BC = 90o , cung CD = 45o .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính chu vi và diện tích tứ giác ABCD theo R.
Hướng dẫn giải
Ta có 
⇒ A, O, D thẳng hàng.
Vì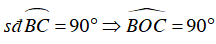 
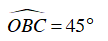
suy ra ΔBOC vuông cân ở O nên: 
Mà 
(góc ở tâm chắn cung AB)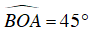
⇒ 
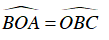
Mà hai góc này ở vị trí so le trong, suy ra BC // AD (1)
Lại có: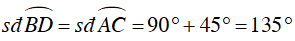 
⇒ BD = AC (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân.
b) Vì tam giác BOC vuông cân tại O nên: BC2 = OB2 + OC2 = 2R2
⇒ 
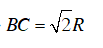
Gọi I là điểm chính giữa của cung BC, nối AI cắt OB tại H.
Dễ thấy ΔAHO vuông cân tại H, có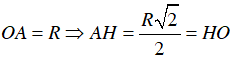 
Do đó: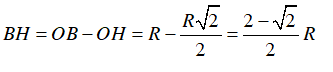 
Xét ΔABH vuông tại H nên:
AB2 = 2 + BH2
⇒ 
, do đó 
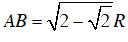
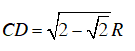
Vậy chu vi hình thang ABCD là:
AB + BC + CD + DA = 
Dễ thấy: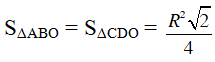 
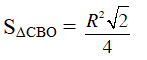
và 
Do đó diện tích của hình thang ABCD là:
.
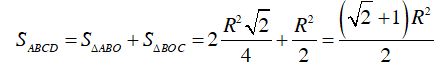
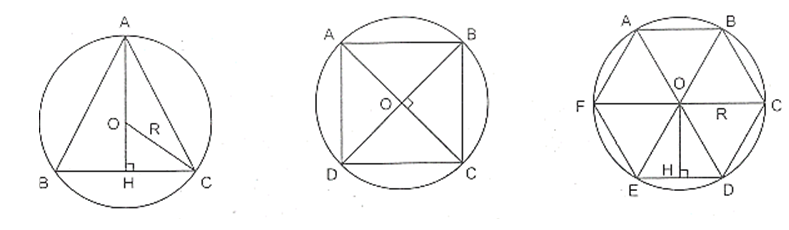
Ví dụ 2 : Một tam giác đều, một hình vuông và một hình lục giác đều cùng nội tiếp đường tròn (O ; R).
a) Tính độ dài mỗi cạnh của các hình trên theo R.
b) Chứng tỏ rằng bán kính của đường tròn nội tiếp lục giác đều bằng một nửa cạnh của tam giác đều.
Hướng dẫn giải
a) Xét tam giác đều ABC nội tiếp đường tròn (O ; R). (h.a)
Kẻ đường cao AH, ta có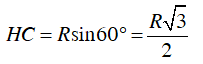 
Do đó BC = 2HC = BC = 2HC =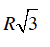 
– Xét hình vuông ABCD nội tiếp đường tròn (O ; R). (h.b)
ΔBOC vuông cân nên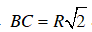 
.
– Xét lục giác đều ABCDEF nội tiếp đường tròn (O ; R). (h.c)
ΔBOC đều nên BC = R.
b) Kẻ OH ⊥ DE (h.c), OH là bán kính của đường tròn nội tiếp lục giác đều.
Ta có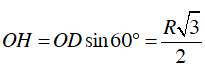 
.
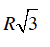
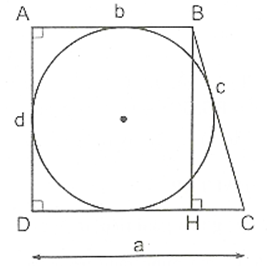
Cạnh của tam giác đều nội tiếp đường tròn (O ; R) bằng , do đó bán kính của đường tròn nội tiếp lục giác đều bằng nửa cạnh của tam giác đều.
Ví dụ 3 : Chứng minh rằng diện tích của một hình thang vuông ngoại tiếp một đường tròn bằng tích của hai cạnh đáy.
Hướng dẫn giải
Xét hình thang ABCD ngoại tiếp đường tròn (O),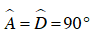 
.
Đặt CD = a, AB = b, BC = c, AD = d.
Kẻ BH ⊥ CD.
Trong tam giác vuông BHC ta có:
BH2 + HC2 = BC2 nên d2 + (a - b)2 = c2 (1)
Do ABCD là tứ giác ngoại tiếp nên a + b = c + d
⇒ c = a + b – d, do đó c2 = (a + b - d)2
Từ (1) và (2) suy ra d2 - (a + b)2 = (a + b - d)2
Vậy diện tích hình thang vuông ngoại tiếp một đường tròn bằng tích của hai cạnh đáy.
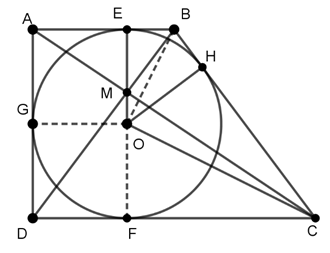
Ví dụ 4 : Cho hình thang vuông ABCD có AB là cạnh đáy nhỏ, CD là cạnh đáy lớn. M là giao điểm của hai đường chéo AC và BD. Biết rằng hình thang ABCD ngoại tiếp đường tròn bán kính R. Tính diện tích tam giác ADM.
Hướng dẫn giải
Gọi O là tâm đường tròn nội tiếp hình thang vuông ABCD. E, F, G, H lần lượt là các tiếp điểm tiếp xúc của đường tròn nội tiếp các cạnh AB, CD, AD, BC. Gọi M là giao điểm của AC và BD.
Giả sử .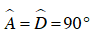
Ta có OB là phân giác của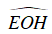 
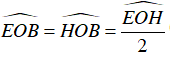
(tính chất hai tiếp tuyến AB và BC cắt nhau)
⇒ 
(1)
OC là phân giác của 
(tính chất hai tiếp tuyến CD và BC cắt nhau)
⇒ 
(2)
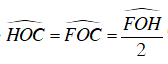
Mà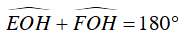 
(hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: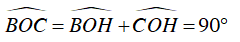 
Xét ΔBOC vuông tại O, có OH ⊥ BC : OH2 = BH.CH
Ta xét tứ giác AEFD có :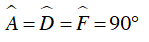 
AEFD là hình chữ nhật
⇒ AE = DF = OE = OH .
Ta có : EB = BH, CF = CH (tính chất hai tiếp tuyến cắt nhau)
⇒ 
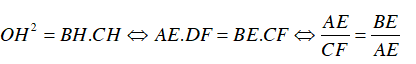
Do đó M nằm trên đoạn EF.
Đường cao ứng với đỉnh M của ΔADM có độ dài R và cạnh đáy là 2R. Suy ra S ΔADM = R2 .
Vì diện tích các tam giác ADM và BCM bằng nhau, nên trong trường hợp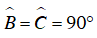 
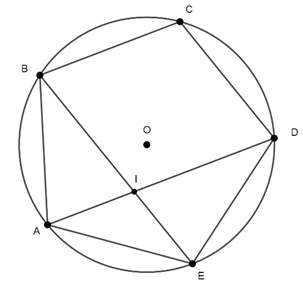
, ta cũng có S ΔBCM = R2 .
Ví dụ 5 : Cho ngũ giác đều ABCDE. Gọi I là giao điểm của AD và BE. Hệ thức nào sau đây đúng. Chứng minh AE2 = AI.AD
Hướng dẫn giải
Ta có: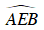 
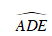
là góc nội tiếp chắn cung AB
là góc nội tiếp chắn cung AE
Mà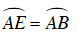 
⇒ 
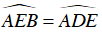
( hai góc nội tiếp chắn hai cung bằng nhau)
Xét ΔAEI và ΔADE , có:
: góc chung
(cmt)
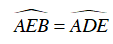
⇒ ΔAEI ∼ ΔADE (g - g)
⇒ 
.
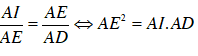
C. Bài tập trắc nghiệm
Câu 1 : Xét các câu sau đây:
(1) Nếu qua bốn đỉnh của một tứ giác có một đường tròn thì tứ giác đó gọi là tứ giác nội tiếp đường tròn.
(2) Trong một tứ giác nội tiếp, tổng số đo hai góc dối diện nhau bằng 1 góc vuông.
(3) Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1 góc vuông thì tứ giác đó nội tiếp được một đường tròn.
(4) Nếu hai đỉnh P, Q liên tiếp cùng nhìn đoạn thẳng MN dưới cùng một góc thì tứ giác MNPQ nội tiếp.
Trong các câu trên:
A. Chỉ có 1 câu đúng
B. Chỉ có 2 câu đúng
C. Chỉ có 3 câu đúng
D. Không có câu nào sai
Hướng dẫn giải
Đáp án B
Trong một tứ giác nội tiếp, tổng số đo hai góc dối diện nhau bằng
Và một tứ giác có tổng hai góc đối diện bằng thì tứ giác đó nội tiếp đường tròn.
Nên (2) và (3) sai.
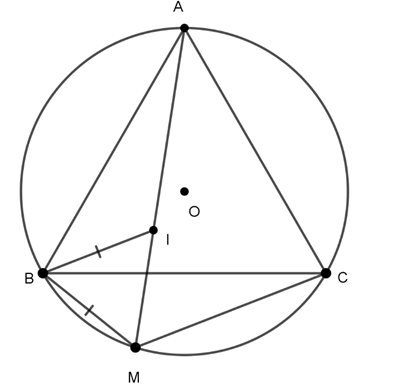
Câu 2 : Cho tam giác ABC nội tiếp đường tròn tâm O (AB < AC). Hai đường cao BE và CF cắt nhau tại H. Tia AO cắt đường tròn tại D.
Xác định câu sai trong các câu sau
A. Tứ giác BHCD là hình bình hành
B. Tứ giác BFEC nội tiếp được đường tròn
C.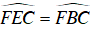 
D. Tứ giác BHCD không nội tiếp được đường tròn.
Hướng dẫn giải
Đáp án C
+ Ta có: A, O, D thẳng hàng nên AD là đường kính. Dó đó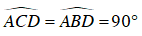 
(góc nội tiếp chắn nửa đường tròn)
⇒ AC ⊥ CD, AB ⊥ BD
Mà BE ⊥ AC , CF ⊥ AB
⊥ BH \\ CD (cùng vuông góc với AC)
Và CH \\ BD (cùng vuông góc với AB)
⇒ BHCD là hình bình hành. Suy ra A đúng.
+ Ta có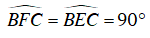 
⇒ E, F là hai đỉnh liên tiếp cùng nhìn BC dưới một góc 90o nên BFEC nội tiếp. Suy ra B đúng.
+ Do BFEC nội tiếp nên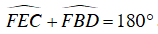 
. Suy ra C sai.
+ Do BHCD là hình bình hành nên không nội tiếp đường tròn. Suy ra D đúng.
Câu 3 : Cho tam giác đều ABC và M là điểm thuộc cung BC ( không chứa A) của đường tròn ngoại tiếp tam giác. Nếu cho MB = 60cm và MC = 90cm thì MA sẽ bằng:
A. 150cm
B. 210cm
C. 30cm
D. 75cm
Hướng dẫn giải
Đáp án A
Trên MA lấy điểm I sao cho BM = BI.
⇒ ΔBMI cân tại B
Mà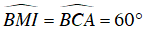 
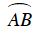
(hai góc nội tiếp cùng chắn 
)
⇒ ΔBMI đều
⇒ IM = BM (1)
Ta lại có:
( ΔABC đều)
(ΕMBI đều)
⇒ 
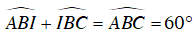
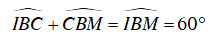
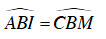
Xét ΔAIB và ΔCMB , ta có:
(hai góc nội tiếp cùng chắn 
)
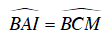
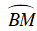
AB = BC ( ΔABC đều)
(cmt)
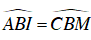
⇒ ΔAIB = ΔCMB (g - c- g)
⇒ AI = CM (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: MA = MB + MC = 60 + 90 = 150 cm
Vậy MA = 150 cm.
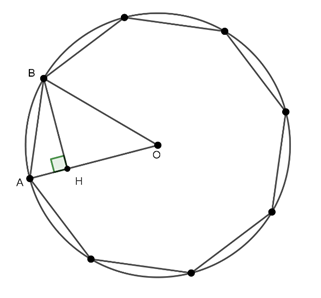
Câu 4 : Tính diện tích của hình 8 cạnh đều nội tiếp trong một đường tròn tâm O, bán kính R.
Hướng dẫn giải
Đáp án C
Ta có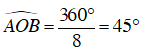 
Từ B kẻ BH ⊥ OA
⇒ ΔOBH vuông cân tại H, ta có: OB2 = OH2 + BH2
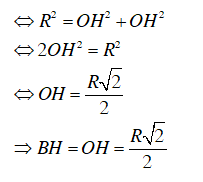
Diện tích tam giác OAB là: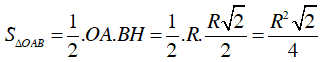 
Gọi S là diện tích của hình 8 cạnh đều, khi đó: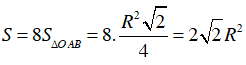 
.
Câu 5 : Tính số cạnh của một đa giác đều nội tiếp đường tròn tâm O, bán kính R, biết độ dài cạnh AB của nó bằng R.
A. 4
B. 5
C. 6
D. 8
Hướng dẫn giải
Đáp án C
Áp dụng công thức: 
Ta có: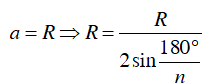 
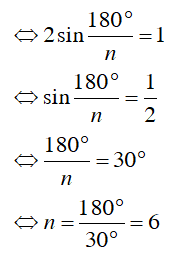
Vậy đa giác đều có sáu cạnh.
