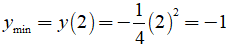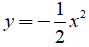Đồ thị hàm số y = ax^2 (a ≠ 0): lý thuyết, các dạng bài tập có đáp án | Toán lớp 9
Đồ thị hàm số y = ax^2 (a ≠ 0): lý thuyết, các dạng bài tập có đáp án
Tài liệu Đồ thị hàm số y = ax^2 (a ≠ 0): lý thuyết, các dạng bài tập có đáp án Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Đồ thị hàm số y = ax^2 (a ≠ 0) từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Đồ thị hàm số y = ax2 (a ≠ 0)
Đồ thị của hàm số y = ax2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất cảu đồ thị.
2. Cách vẽ đồ thị hàm số y = ax2 (a ≠ 0)
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số y =ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
3. Ví dụ cụ thể
Câu 1: Vẽ đồ thị hàm số y = x2.
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = x2 | 0 | 1 | 1 | 4 | 4 |
Trên mặt phẳng tọa độ, lấy các điểm O(0;0): A(1; 1); B (-1; 1); C(2; 4) và D( -2;4) rồi lần lượt nối chúng để được đường cong như hình dưới đây.
Đồ thị của hàm số y = x2:
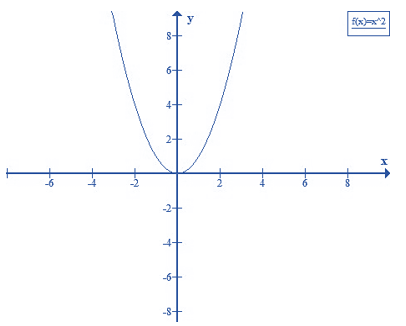
Câu 2: Vẽ đồ thị hàm số y = -(1/2)x2
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = -(1/2)x2 | 0 | -1/2 | -1/2 | -2 | -2 |
Đồ thị
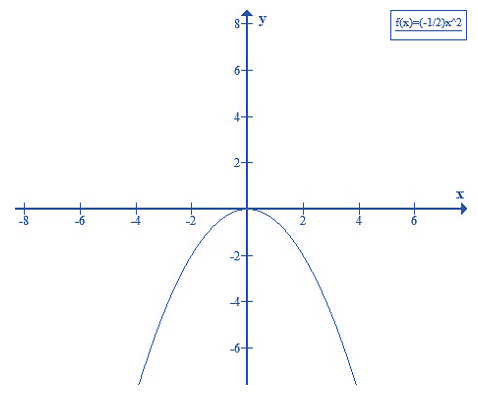
Trên mặt phẳng tọa độ lấy các điểm
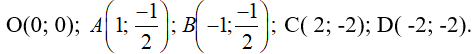
Nối các điểm đó ta được đường cong như hình vẽ dưới đây là đồ thị hàm số

B. Bài tập tự luận
Câu 1: Cho hàm số y = ax2 . Tìm giá trị nhỏ nhất của y khi x đi từ -2017 đến 2018
Lời giải:
Ta thấy rằng hệ số a của đồ thị này dương, nên đồ thị có giá trị nhỏ nhất là y = 0 tại x = 0
Nhận thấy rằng trong khoảng -2017 đến 2018 đi qua hoành độ x = 0
Do đó giá trị nhỏ nhất của hàm số y = ax2 là y(0) = 0
Vậy giá trị nhỏ nhất của y bằng 0 tại x = 0
Câu 2: Cho hàm số 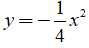
Lời giải:
Hệ số a của đồ thị này là số âm nên đồ thị này có giá trị lớn nhất là
* Khi x đi từ -1 đến 0 thì hàm số đồng biến nên trên đoạn [-1; 0] , hàm số đạt giá trị nhỏ nhất tại x = -1 và 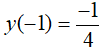
* Khi x đi từ 0 đến 2 thì hàm số nghịch biến nên hàm số đạt giá trị nhỏ nhất tại x = 2 trên đoạn
[ 0; 2] và y(2) = -1
* Suy ra, hàm số đạt giá trị nhỏ nhất tại x = 2 và