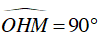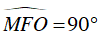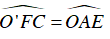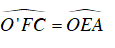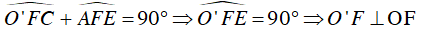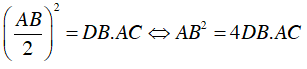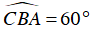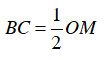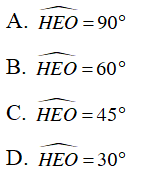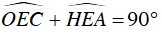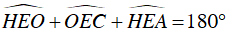Cách chứng minh tiếp tuyến của một đường tròn cực hay, chi tiết | Toán lớp 9

---

Cách chứng minh tiếp tuyến của một đường tròn cực hay, chi tiết

Với Cách chứng minh tiếp tuyến của một đường tròn cực hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chứng minh tiếp tuyến của một đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Để chứng minh đường thẳng d là tia tiếp tuyến của đường tròn (O;R) tại điểm A ta dùng các cách sau đây:

Cách 1: Kẻ OA ⊥ d tại A, chứng minh OA = R.

Cách 2: Đường thẳng d đi qua A ∈ (O ; R) thì ta cần chứng minh OA ⊥ d tại điểm A.

B. Ví dụ minh họa

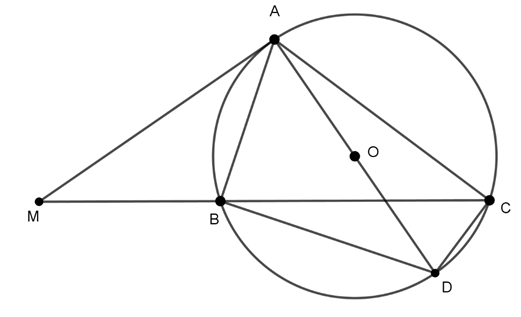
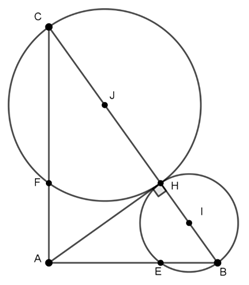
Ví dụ 1 : Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA² = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

Vì MA² = MB.MC ⇒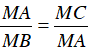

Xét ΔMAC và ΔMBA có

: góc chung

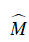
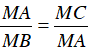
⇒ ΔMAC ∼ ΔMBA (c.g.c)

⇒ (1)

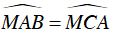
Kẻ đường kính AD của (O)

Ta có 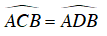(hai góc nội tiếp cùng chắn cung AB )

Mà 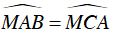(chứng minh trên)

Suy ra 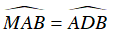(3)

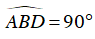
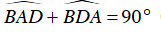
Lại có (góc nội tiếp chắn nửa đường tròn)

⇒ (4)

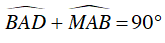
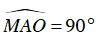
Từ (3) và (4) suy ra hay

⇒ OA ⊥ MA

Do A ∈ (O)

⇒ MA là tiếp tuyến của (O).

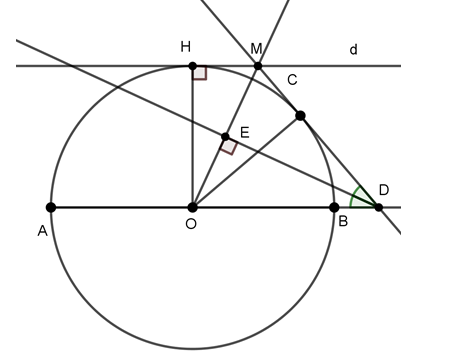
Ví dụ 2 : Cho đường tròn tâm O đường kính AB. C là một điểm thay đổi trên đường tròn (O). Tiếp tuyến tại C của (O) cắt AB tại D. Đường thẳng qua O và vuông góc với phân giác của 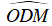, cắt CD tại M. Qua M kẻ đường thẳng d song song với AB. Chứng minh d là tiếp tuyến của (O).

Hướng dẫn giải

Kẻ OH ⊥ d ⇒

Ta có CD là tiếp tuyến của (O) nên OC ⊥ CD tại C ⇒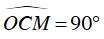

Gọi E là giao điểm của tia phân giác 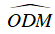với OM

Xét tam giác MDO có : DE là phân giác 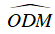, DE là đường cao

⇒ ΔDOM cân tại D

⇒ (hai góc ở đáy)

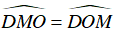
Ta lại có : d//AB ⇒ 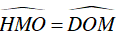(hai góc so le trong)

⇒

Xét ΔOHM và ΔOCM , có :

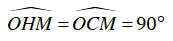
OM: cạnh chung

(cmt)

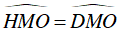
⇒ ΔOHM = Δ OCM (cạnh huyền – góc nhọn)

⇒ OH = OC = R (hai cạnh tương ứng)

⇒ H ∈ (O;R)

Do đó d là tiếp tuyến của (O;R).

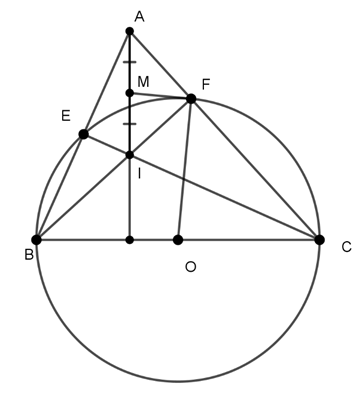
Ví dụ 3 : Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).

Hướng dẫn giải

Ta có : 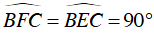(góc nội tiếp chắn nửa đường tròn)

⇒ BF ⊥ AC , CE ⊥ AB

Xét tam giác ABC, có BF ∩ CE = {I}

⇒ I là trực tâm tam giác ABC

Gọi H là giao điểm của AI với BC

⇒ AH ⊥ BC tại H

Xét tam giác AFI vuông tại F, có M là trung điểm của AI

⇒ FM = MA = MI

⇒ ΔFMA cân tại M

⇒ (hai góc ở đáy) (1)

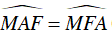
Xét tam giác OFC, có OF = OC

⇒ FOC cân tại O

⇒ (hai góc ở đáy) (2)

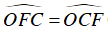
Xét tam giác AHC vuông tại H, có: 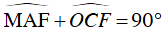(hai góc phụ nhau)(3)

Từ (1), (2) và (3)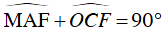

Mà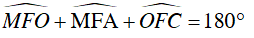

⇒

⇒ MF ⊥ OF

Vậy MF là tiếp tuyến của (O).

C. Bài tập trắc nghiệm

Câu 1 : Cho nửa đường tròn tâm O đường kính AB. Ax, By là hai tiếp tuyến của (O) (Ax, By cùng phía đối với đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho

.

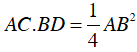
Khi đó:

a. CD tiếp xúc với đường tròn (O)

b. CD cắt đường tròn (O) tại hai điểm phân biệt

c. CD không có điểm chung với (O)

d. CD = R²

Hướng dẫn giải

Đáp án A

Trên tia đối của tia BD lấy điểm E sao cho BE = AC

Kẻ OH ⊥ CD

Ta có: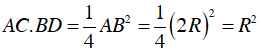

Mà AC = BE ⇒ BE.BD = R² = OB²

⇒ ΔDOE vuông tại O

Xét ΔOAC và ΔOBE , ta có:

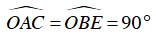
AC = BE (gt)

OA = OB (=R)

⇒ ΔOAC = ΔOBE (g-g-g)

⇈ (hai góc tương ứng)

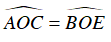
Ta có: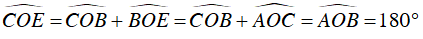

Nên C, O, E thẳng hàng

Xét tam giác DCE, có:

OD vừa là đường cao vừa là đường trung tuyến của △CDE nên OD cũng là đường phân giác.

⇒ (DO là phân giác )

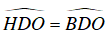
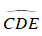
Xét ΔOHD và ΔOBD , có:

OD chung

(Cmt)

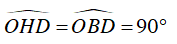
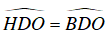
⇒ ΔOHD = ΔOBD (cạnh huyền - góc nhọn)

⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).

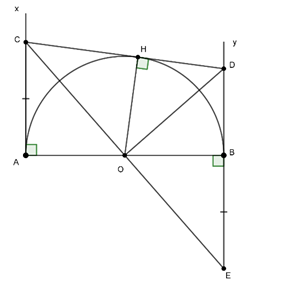
Câu 2 : Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau ở I. Khi đó:

a. AK là tiếp tuyến của đường tròn đường kính AI

b. BK là tiếp tuyến của đường tròn đường kính AI

c. BH là tiếp tuyến của đường tròn đường kính AI

d. HK là tiếp tuyến của đường tròn đường kính AI

Hướng dẫn giải

Đáp án D

Gọi O là trung điểm của AI, khi đó: KO là đường trung tuyến của tam giác vuông AKO.

⇒ AO = IO = OK.

⇒ ΔOAK cân tại O

⇒ (hai góc ở đáy) (1)

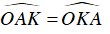
Xét tam giác BKC vuông tại K, có H là trung điểm của BC(do tam giác ABC cân tại A)

⇒ BH = HK = HC.

⇒ ΔHCK cân tại H

⇒ (hai góc ở đáy) (2)

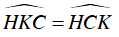
Ta lại có: 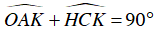(hai góc nhọn phụ nhau trong tam giác vuông AHC)(3)

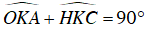
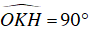
Từ (1), (2) và (3) suy ra: hay

Từ đó suy ra rằng HK là tiếp tuyến của đường tròn đường kính AI.

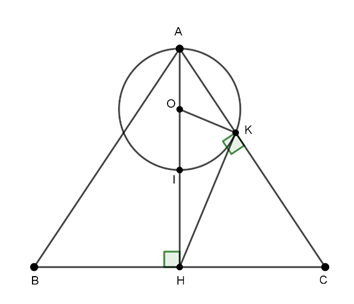
Câu 3 : Cho đường tròn (O) đường kính AB, lấy điểm M sao cho A nằm giữa B và M. Kẻ đường thẳng MC tiếp xúc với đường tròn (O) tại C. Từ O hạ đường thẳng vuông góc với CB tại H và cắt tia MC tại N. Khẳng định nào sau đây không đúng?

a. BN là tiếp tuyến của đường tròn (O)

b. BC là tiếp tuyến của đường tròn (O)

c. OC là tiếp tuyến của đường tròn (O, ON)

d. AC là tiếp tuyến của đường tròn (C, BC)

Hướng dẫn giải

Đáp án A

+ BC là dây của đường tròn (O), nên B sai.

+ Ta có 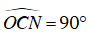⇒ ΔOCN nội tiếp đường tròn đường kính ON

⇒ OC là dây của đường tròn đường kính ON, nên C sai.

+ Ta có AC là đường thẳng đi qua tâm của (C,BC) nên không thể là tiếp tuyến. Do đó D sai.

+ Ta có OH ⊥ BC

Xét tam giác OBC cân tại O (OB = OC) có OH là đường cao

⇒ OH là phân giác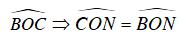

Xét ΔOCN và ΔOBN , ta có :

OC = OB

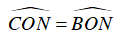
ON : cạnh chung

⇒ ΔOCN = ΔOBN (c-g-c)

⇒ (hai góc tương ứng)

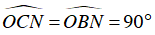
⇒ BN ⊥ OB

Vậy BN là tiếp tuyến của đường tròn (O).

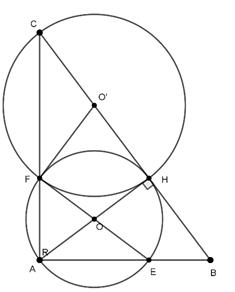
Câu 4 : Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm O đường kính AH cắt AB tại E, đường tròn tâm O’ đường kính HC cắt AC tại F. Khi đó:

a. EF là tiếp tuyến của đường tròn (H, HO)

B, O’F là tiếp tuyến của đường tròn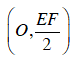

c. EF là tiếp tuyến chung của hai đường tròn (O) và (O’).

d. OF là tiếp tuyến của đường tròn (C, CF).

Hướng dẫn giải

Đáp án

EF không vuông góc với OH nên EF không là tiếp tuyến của (H,HO).

EF là không là tiếp tuyến chung của hai đường tròn (O) và (O’).

EF không vuông góc với CF nên EF không là tiếp tuyến của (C,CF).

Xét tam giác O’CF cân tại O’(O’C = O’F)

⇒ (hai góc ở đáy)

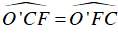
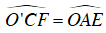
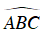
Ta lại có: (hai góc cùng phụ )

⇒

Mà 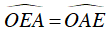( ΔOAE cân tại O)

⇒

Mà 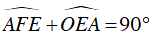(hai góc phụ nhau trong tam giác vuông AEF)

⇒

Vậy O’F là tiếp tuyến của đường tròn .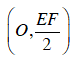

Câu 5 : Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn dựng hai tiếp tuyến Ax và By. Trên tia Ax lấy điểm C, trên tia Ay lấy điểm D. Điều kiện cần và đủ để CD tiếp xúc với đường tròn (O) là:

A. AB² = AC.BD

B. AB² = 2AC.BD

C. AB² = 4AC.BD

D. AB² = AC².BD²

Hướng dẫn giải

Đáp án C

( ⇒ ) CD tiếp xúc với đường tròn (O)

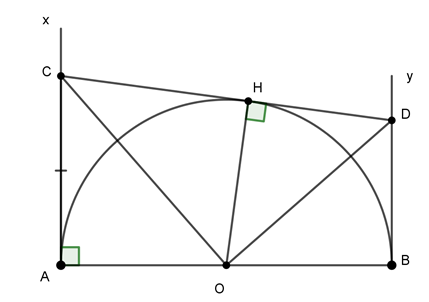
CD là tiếp tuyến của (O) tại H

CD cắt Ax tại C, theo tính chất hai tiếp tuyến cắt nhau, ta có:

AC = CH và OC là tia phân giác của 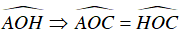(1)

CD cắt By tại D, theo tính chất hai tiếp tuyến cắt nhau, ta có:

và OD là phân giác của 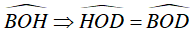(2)

Từ (1) và (2) suy ra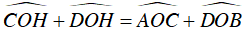

Ta lại có: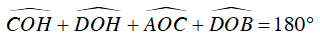

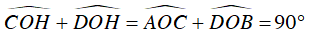
Xét tam giác COD vuông tại O, OH ⊥ CD :

OH² = DH.CH = DB.AC

⇔

(⇐)

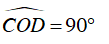
Kẻ OH ⊥ CD

Trên tia đối của tia BD lấy điểm E sao cho BE = AC

Ta có: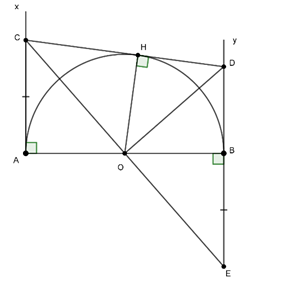

Mà AC = BE ⇒ BE.BD = R² = OB²

⇒ ΔDOE vuông tại O

Xét ΔOAB và ΔOBE , ta có:

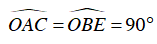
AC = BE (gt)

OA = OB (=R)

⇒ ΔOAB = ΔOBE

⇒ (hai góc tương ứng)

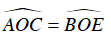
Ta có: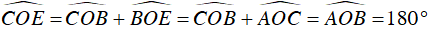

Nên C, O, E thẳng hàng

Xét tam giác DCE, có:

OD vừa là đường cao vừa là đường trung tuyến của ΔCDE nên OD cũng là đường phân giác.

⇒ (DO là phân giác )

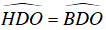
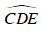
Xét ΔOHD và ΔOBD , có:

OD chung

(Cmt)

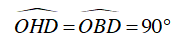
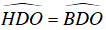
⇒ ΔOHD = ΔOBD (cạnh huyền - góc nhọn)

⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).

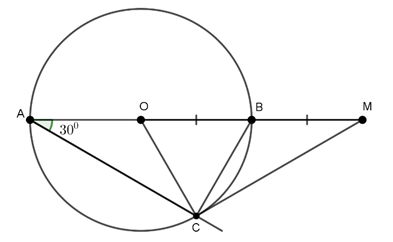
Câu 6 : Cho đường tròn (O, R) đường kính AB. Vẽ dây cung AC sao cho góc CAB bằng 30^o . Trên tia đối của tia BA lấy điểm M sao cho BM = R. Khi đó:

a. AM là tiếp tuyến của đường tròn (O).

b. BM là tiếp tuyến của đường tròn (O).

c. CM là tiếp tuyến của đường tròn (O).

d. AB là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

Đáp án C

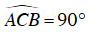
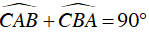
Ta có: (góc nội tiếp chắn nửa đường tròn)

⇒(hai góc phụ nhau)

⇒

Xét tam giác OBC có OB = OC và

⇒ ΔOBC đều

⇒ OB = BC = BM

⇒

⇒ ΔOCM vuông tại C

⇒ ⇒ OC ⊥ CM

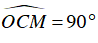
Vậy CM là tiếp tuyến của đường tròn (O).

Câu 7 : Trong các phát biểu dưới đây, phát biểu nào sau đây đúng:

A. Đường thẳng d được gọi là tiếp tuyến của (O) khi chúng có điểm chung

B. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A

C. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và A thuộc (O)

D. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và OA > R.

Hướng dẫn giải

Đáp án C

Theo định nghĩa của tiếp tuyến, Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và OA = R.

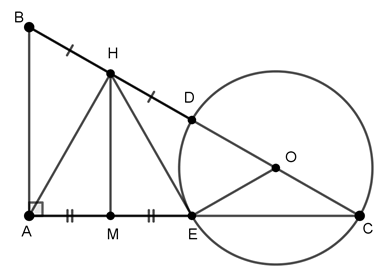
Câu 8 : Cho tam giác ABC vuông ở A. Vẽ đường cao AH, gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD cắt CA ở E, O là trung điểm của CD Khi đó, góc HEO bằng:

Hướng dẫn giải

Đáp án A

Gọi O là tâm đường tròn đường kính CD

E nằm trên đường tròn đg kính CD

⇒ ΔDE vuông tại E

⇒ ⇒ DE ⊥ EC

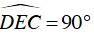
Mà AB AC (do tam giác ABC vuông tại A)

⇒ DE // AB ( từ vuông góc đến song song)

⇒ ABDE là hình thang

Gọi M là trung điểm của AE

Ta có: H là trung điểm của BD (D đối xứng với B qua H)

⇒ HM là đg trung bình của hình thang ABDE

⇒ HM // AB HM ⊥ AC

Xét ΔAHE có HM vừa là đường trung tuyến, vừa là đường cao

⇒ ΔAHE cân tại H ⇒ 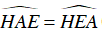( Hai góc ở đáy)

+ ΔCOE cân tại O ⇒ 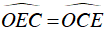(hai góc ở đáy)

Mà (hai góc phụ nhau trong tam giác vuông AHC)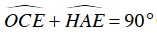

⇒

Mà

⇒ .

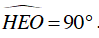
Câu 9 : Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm I đường kính BH cắt AB tại E, đường tròn tâm J đường kính HC cắt AC tại F. Khi đó:

A. EH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H

B. BH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H

C. AH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H

D. CH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H

Hướng dẫn giải

Đáp án C

Ta nhận thấy H ∈ (I), H ∈ (J)

Mà AH ⊥ JH , AH ⊥ IH

Suy ra AH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H.

Câu 10 : Cho tam giác ABC có AB=3cm, AC=4cm và BC=5cm. Khi đó:

A. AB là tiếp tuyến của (C;3cm).

B. AC là tiếp tuyến của (B;3cm).

C. AB là tiếp tuyến của (B;4cm).

D. AC là tiếp tuyến của (C;4cm).

Hướng dẫn giải

Đáp án B

Vì AB = 3cm ⇒ A ∈ (B;3cm).

Xét tam giác ABC, có :

BC² = 5² = 25

AB² + AC² = 3² + 4² = 9 + 16 = 25

⇒ AB² + AC² = BC²

Theo định lý Py – ta – go đảo suy ra tam giác ABC vuông tại A

⇒ AB ⊥ AC

⇒ AC là tiếp tuyến của (B;3cm).