Lý thuyết Giải bài toán bằng cách lập phương trình hay, chi tiết | Toán lớp 9

Lý thuyết Giải bài toán bằng cách lập phương trình hay, chi tiết

Tài liệu Lý thuyết Giải bài toán bằng cách lập phương trình hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Giải bài toán bằng cách lập phương trình từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Các bước giải toán

Các bước giải bài toán bằng cách lập phương trình:

Bước 1: Lập phương trình:

    + Chọn ẩn và đặt điều kiện thích hợp cho chúng

    + Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.

    + Lập phương trình biểu thị mối quan hệ giữa các đại lượng .

Bước 2: Giải phương trình nói trên.

Bước 3: Trả lời: kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thích hợp với bài toán và kết luận.

2. Ví dụ cụ thể

Câu 1: Cho một bể cạn (không có nước). Nếu hai vòi nước cùng được mở để chảy vào bể này thì sẽ đầy bể sau 4 giờ 48 phút. Nếu mở riêng từng vòi chảy vào bể thì thời gian vòi một chảy đầy bể sẽ ít hơn thời gian vòi hai chảy đầy bể là 4 giờ. Hỏi mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể?

Hướng dẫn:

Đổi 4 giờ 48 phút = 24/5 (giờ)

Gọi thời gian vòi một chảy một mình đầy bể là x (giờ, x > 24/5)

Khi đó trong một giờ vòi một chảy được 1/x (phần bể)

Vòi hai chảy một mình đầy bể trong x + 4 (giờ) nên trong một giờ chảy được: 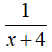(phần bể)

Tổng cộng trong một giờ hai vòi chảy được 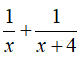(phần bể) (3)

Sau 4 giờ 48 phút = 24/5 giờ hai vòi cùng chảy thì đầy bể nên trong một giờ chảy được 5/24 (phần bể) (4)

Từ (3) và (4) ta có phương trình

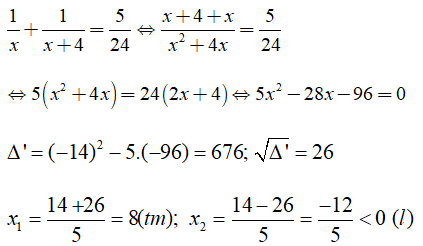
Vậy thời gian vòi một chảy một mình đầy bể là 8 giờ. Vòi hai chảy một mình đầy bể là 8 + 4 = 12 (giờ).

Câu 2: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài lớn hơn chiều rộng là 7m. Tính chiều dài và chiều rộng của mảnh đất đó.

Hướng dẫn:

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m, x > 0; x < 13)

Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)

Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:

x² + (x + 7)² = 13² ⇔ 2x² + 14x - 120 = 0

Ta có:

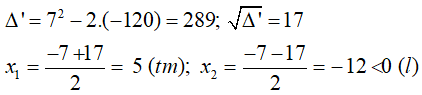
Giải phương trình ta được x = 5 hoặc x = -12. Đối chiếu với điều kiện ta có chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.

B. Bài tập tự luận

Câu 1: Một người dự định đi xe đạp từ địa điểm A tới địa điểm B cách nhau 36km trong một thời gian nhất định. Sau khi đi được nửa quãng đường, người đó dừng lại nghỉ 18 phút. Do đó để đến B đúng hạn, người đó đã tăng thêm vận tốc 2km trên quãng đường còn lại. Tính vận tốc ban đầu và thời gian thực tế xe lăn bánh trên đường.

Lời giải:

Đổi đơn vị: 18 phút = 3/10 giờ

Gọi vận tốc dự định của người đó là x (km/ h; x > 0)

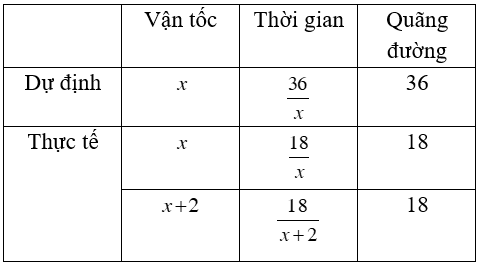
Ta có phương trình :

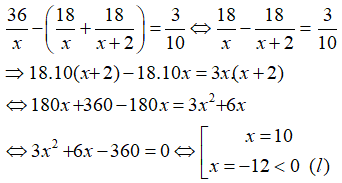
Vậy vận tốc ban đầu là 10 km/h

Thời gian xe lăn bánh trên đường là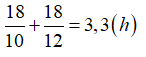

Câu 2: Một ca nô đi xuôi dòng nước từ bến A đến bến B, cùng lúc đó một người đi bộ đi từ bến A dọc theo bờ sông về hướng B. Sau khi chạy được 24 km, ca nô quay trở lại và gặp người đi bộ tại địa điểm C cách bến A 18km. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc của người đi bộ và vận tốc dòng nước đều bằng 4km/h.

Lời giải:

Gọi vận tốc của cano khi nước yên lặng là x (km/h; x > 4).

Vận tốc cano khi xuôi dòng là: x + 4( km/h). Thời gian đi xuôi dòng là: 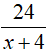( h)

Vận tốc cano khi ngược dòng là: x - 4 ( km/h).

Vì ca no gặp người tại địa điểm C cách A 18 km nên quãng đường BC = 24 – 18 = 6km.

Thời gian cano đi ngược dòng từ B đến C là: 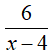(h)

Thời gian của người đi bộ kể từ khi xuất phát đến khi gặp cano là: 18/4 ( h)

Vì cano và người đi bộ khởi hành cùng lúc nên ta có phương trình:

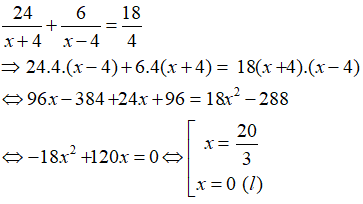
Vậy vận tốc cần tìm là 20/3 (km/h)