Lý thuyết Vị trí tương đối của hai đường tròn (tiếp theo) hay, chi tiết | Toán lớp 9

Lý thuyết Vị trí tương đối của hai đường tròn (tiếp theo) hay, chi tiết

Tài liệu Lý thuyết Vị trí tương đối của hai đường tròn (tiếp theo) hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Vị trí tương đối của hai đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Ba vị trí tương đối của hai đường tròn.

a) Hai đường tròn cắt nhau.

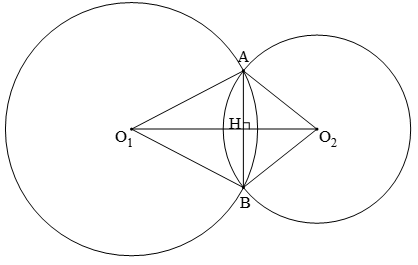
Hai đường tròn có hai điểm chung được gọi là hai đường tròn cắt nhau.

    + Hai điểm A, B là hai giao điểm.

    + Đoạn thẳng AB là dây chung.

    + Đặt O₁A = R; O₂A = r khi đó: |R - r| < O₁O₂ < R + r

    + Đường thẳng O₁O₂ là đường nối tâm, đoạn thẳng O₁O₂ là đoạn nối tâm.

    + Tính chất đường nối tâm: Đường nối tâm là đường trung trực của dây chung

b) Hai đường tròn tiếp xúc nhau.

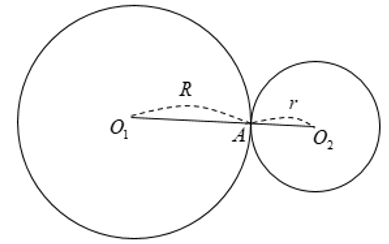
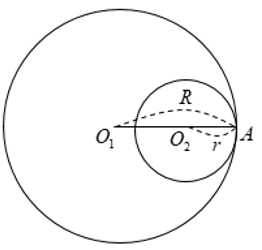
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc.

    + Điểm A gọi là tiếp điểm.

    + Có hai trường hợp tiếp xúc của hai đường tròn:

     ⋅ Tiếp xúc ngoài tại A: O₁O₂ = R + r

     ⋅ Tiếp xúc trong tại A: O₁O₂ = |R - r|

c) Hai đường tròn không giao nhau

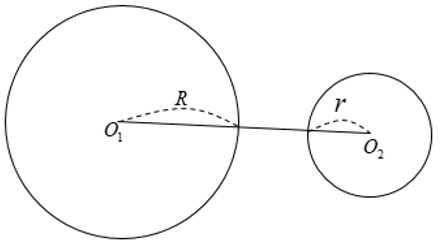
Hai đường tròn không có điểm chung nào được gọi là hai đường tròn không giao nhau.

    + Hai đường tròn ngoài nhau: O₁O₂ > R + r

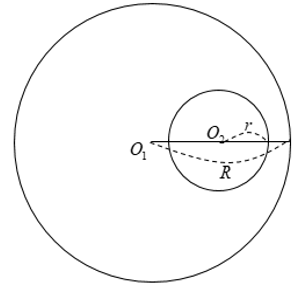
    + Hai đường tròn đựng nhau: O₁O₂ < |R - r|

    + Đặc biệt, khi (O₁) và (O₂) đồng tâm: O₁O₂ = 0

2. Định lý

    + Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung.

    + Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.

3. Tiếp tuyến chung của hai đường tròn

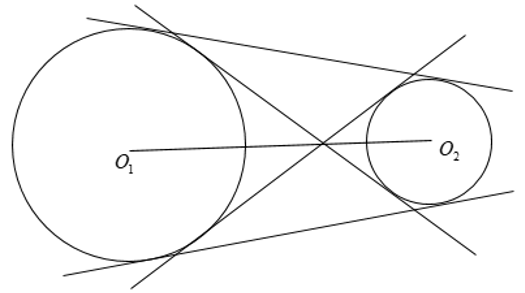
    + Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.

    + Tiếp tuyến chung ngoài không cắt đường nối tâm.

    + Tiếp tuyến chung trong cắt đường nối tâm.

4. Ví dụ cụ thể

Câu 1: Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA. Xác định tính tương đối của hai đường tròn

Hướng dẫn:

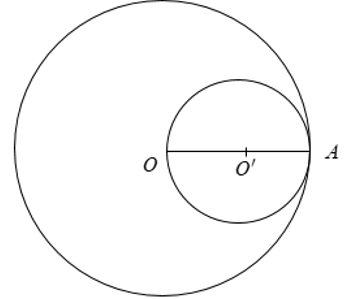
Gọi đường tròn (O') là đường tròn đường kính OA.

Ta có: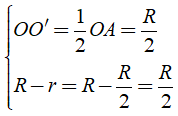

⇒ (O) và (O') tiếp xúc trong.

B. Bài tập tự luận

Câu 1: Cho hai đường tròn (O; 20) và (O'; 15) cắt nhau tại A và B. Tính đoạn thẳng nối OO' biết rằng AB = 24

Lời giải:

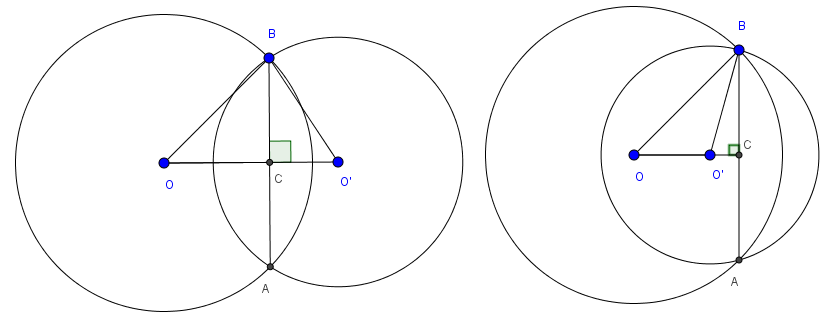
Ta có 2 trường hợp xảy ra:

Gọi C là giao điểm của đường thẳng AB và OO'

Câu 2: Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại hai điểm A và B. Vẽ đường kính AOC và đường kính AO'D

a) Chứng minh ba điểm C, B, D thẳng hàng

b) Qua A vẽ cát tuyến cắt (O) và (O') lần lượt tại M và N. CMR: MN ≤ CD

Lời giải:

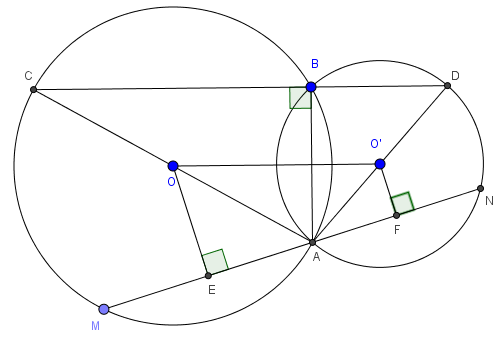
a) Tam giác ABC có AC là đường kính nên tam giác ABC vuông tại B hay AB ⊥ BC

Tam giác ABD có AD là đường kính nên tam giác ABD vuông tại B hay AB ⊥ BD

⇒ C, B, D cùng thuộc đường thẳng qua B và vuông góc với AB

b) Xét tam giác ACD có OO' là đường trung bình nên OO' = 1/2 CD

Gọi E, F lần lượt là hình chiếu của O và O' nên MN

Khi đó E, F lần lượt là trung điểm của AM và AN

⇒ EF = 1/2 MN

Ta đưa việc so sánh CD với MN qua so sánh OO' với EF

Xét 2 đường thẳng OE và O'F song song với nhau.

EF vuông góc với cả hai đoạn thẳng nên EF là đoạn thẳng nhỏ nhất trong các đoạn nối từ 1 điểm trên OE tới 1 điểm trên O'F. Khi đó: EF ≤ OO' ⇒ MN ≤ CD