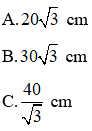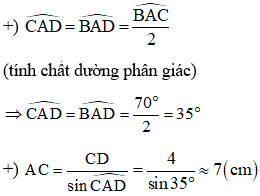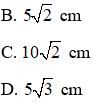Giải tam giác vuông biết độ dài một cạnh và số đo một góc nhọn | Toán lớp 9

Giải tam giác vuông biết độ dài một cạnh và số đo một góc nhọn

Với Giải tam giác vuông biết độ dài một cạnh và số đo một góc nhọn Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giải tam giác vuông biết độ dài một cạnh và số đo một góc nhọn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

Nhắc lại kiến thức

Trong một tam giác vuông, nếu cho trước hai cạnh hoặc một cạnh và một góc nhọn thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của nó. Bài toán đặt ra như thế được gọi là bài toán "Giải tam giác vuông".

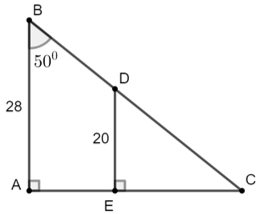
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c.

1. Định lý: Trong một tam giác vuông, mỗi cạnh góc vuông bằng

- Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

- Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.

2. Như vậy, trong tam giác ABC vuông tại A, ta có hệ thức

• b = a.sinB = a.cosC = c.tanB = c.cotC

• c = a.sinC = a.cosB = b.tanC = b.cotB

A. Phương pháp giải

• Xác định cạnh kề, cạnh đối. Viết tỉ số lượng giác để tìm độ dài các cạnh.

• Tính góc nhọn còn lại nhờ quan hệ phụ nhau.

• Thay giá trị rồi tính.

B. Ví dụ minh họa

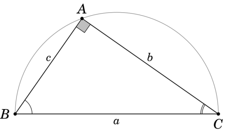
Ví dụ 1: Cho tam giác ABC vuông tại A có AB = 21 cm, 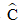= 40^o. Hãy tính độ dài:

a) AC, BC

b) Đường phân giác BD.

Hướng dẫn giải:

a) Xét tam giác ABC vuông tại A có:

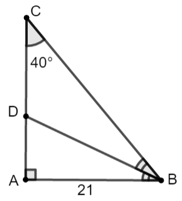
Ví dụ 2: Cho hình vẽ sau, biết 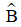= 50^o, cạnh DE = 20 cm, AB = 28 cm. Tính độ dài đoạn AE.

+) Xét tam giác ABC vuông tại A có:

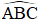
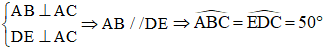
AC = AB.tan = AB.tan50^o ≈ 28.1,19 = 33,32 (cm)

+) (hai góc ở vị trí đồng vị)

+) Xét tam giác DEC vuông tại E có:

EC = ED.tan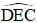 = 20.tan50^o ≈ 20.1,19 = 23,8 (cm)

Vậy AE = AC – EC = 33,32 – 23,8 = 9,52 (cm)

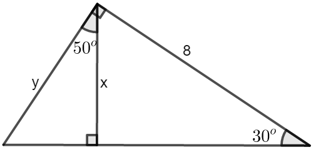
Ví dụ 3: Tìm x, y trong hình sau:

Hướng dẫn giải:

Ta có:

C. Bài tập trắc nghiệm

Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 23cm, 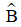= 50^o . Tính độ dài AC.

A. 38 cm

B. 35,78 cm

C. 39 cm

D. 34,12 cm

Hướng dẫn giải:

Xét tam giác ABC vuông tại A, có:

= 90^o - 50^o = 40^o

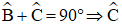
Xét tam giác AHC vuông tại H có:

AH = AC.sin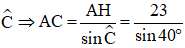 = 35,78 cm

Đáp án B.

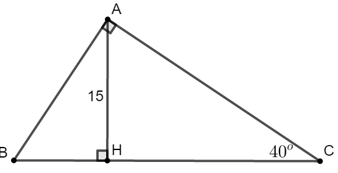
Bài 2: Cho hình vẽ sau. Tam giác ABC vuông tại A, đường cao AH. Biết AH = 15cm, 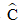= 40^o. Tính độ dài AB.

A. 19,58 cm

B. 21,01 cm

C. 20,15 cm

D. 18,67 cm

Hướng dẫn giải:

+) Xét tam giác AHC vuông tại H, có:

AH = AC.sin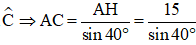 ≈ 23,34cm

+) Xét tam giác ABC vuông tại A có:

AB = AC.tan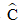 = 23,34.tan40^o ≈ 19,58

Đáp án A.

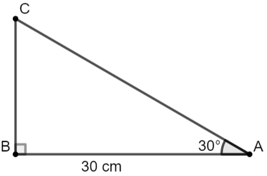
Bài 3: Cho tam giác ABC vuông tại B, có AB = 30 cm, 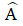= 30^o. Tính cạnh AC.

D. 60 cm

Hướng dẫn giải:

Xét ΔABC vuông tại B có: AC = 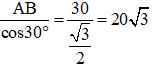(cm)

Đáp án A.

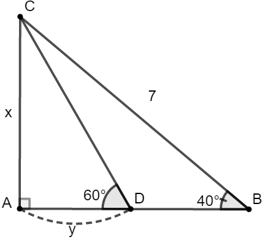
Bài 4: Tìm x, y trong hình vẽ dưới đây

A. x = 4,2 và y = 5

B. x = 5 và y = 4,2

C. x = 4,5 và y =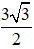

D. x = 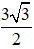và y = 4,5

Hướng dẫn giải:

+) Xét ΔABC vuông tại A có:

AC = BC.sin40^o ⇒ x ≈ 7.0,643 ≈ 4,5

+) Xét ΔADC vuông tại A có:

AD =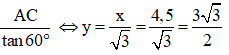

Đáp án C.

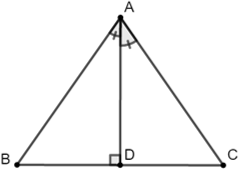
Bài 5: Cho tam giác ABC cân tại A, góc A có số đo bằng 70^o. Đường phân giác AD cắt BC ở D. Tính độ dài cạnh AC biết CD = 4 cm.

A. 7 cm

B. 2,3 cm

C. 3,76 cm

D. 4,3 cm

Hướng dẫn giải:

Do ΔABC cân ở A có AD là đường phân giác ⇒ AD đồng thời là đường cao của tam giác ⇒ AD ⊥ BC ⇒ ΔADC là tam giác vuông ở D.

Xét ΔADC vuông ở D có:

Đáp án A

Bài 6: Cho tam giác ABC vuông ở A có 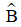= 45^o, biết BC = 10 cm. Tính độ dài đoạn thẳng AB, AC.

A. 5 cm

Hướng dẫn giải:

Tam giác vuông ABC có 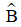= 45^o là tam giác vuông cân tại A

⇒ AB = AC

Ta có: AB = BC.sin45^o = 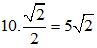(cm)

⇒ AB = AC = 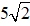cm

Đáp án B.

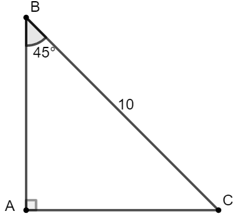
Bài 7: Một em học sinh đứng ở mặt đất cách tháp ăng – ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20^o so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tháp.

A. 54,6 m

B. 56,1 cm

C. 54,6 cm

D. 56,1 m

Hướng dẫn giải:

Gọi E là vị trí mà em học sinh đứng. B là vị trí của mắt.

Ta có: AB = 150 m, AD = BE = 1,5 m và 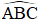= 20^o

Vậy chiều cao của tháp là đoạn thẳng CD.

+) Xét tam giác ABC vuông tại A có:

AC = AB.tan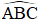 ⇒ AC = 150.tan20^o ≈ 54,6 (m)

⇒ CD = AC + AD = 54,6 + 1,5 = 56,1 (cm)

Đáp án D.

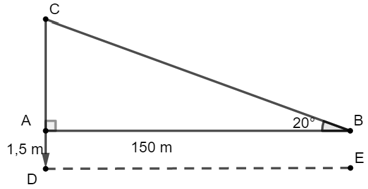
Bài 8: Thang AB dài 7 m tự vào tường làm thành góc 67^o so với mặt đất. Hỏi chiều cao của thang là bao nhiêu so với mặt đất?

A. 7,61 m

B. 5,56 m

C. 7 m

D. 6,44 m

Hướng dẫn giải:

Chiều dài cái thang chính là độ dài đoạn thẳng BC.

Xét ΔABC vuông tại B có:

BC = AC.sin67^o ⇒ BC ≈ 7.0,92 = 6,44 (m) (m)

Vậy cái thang cao 6,44m so với mặt đất.

Đáp án D.

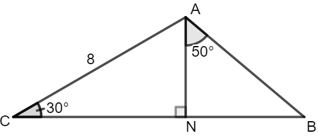
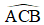
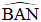
Bài 9: Cho hình vẽ sau, biết AC = 8; = 30^o, = 50^o. Tính AB ?

A. AB ≈ 3,6

B AB ≈ 5,2

C. AB ≈ 3,2

D. AB ≈ 6,2

Hướng dẫn giải:

Tam giác CAN vuông tại N, có sinC = 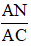⇒ AN = AC.sinC = 8.sin30^o

Tam giác ABN vuông tại N, có cos = 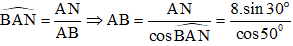≈ 6,2

Đáp án D.

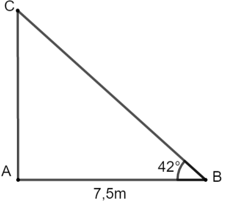
Bài 10: Một cột đèn có bóng trên mặt đất dài 7,5m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42^o. Tính chiều cao của cột đèn (làm tròn đến chữ số thập phân thứ hai)

A. 6,753m

B. 6,75m

C. 6,751m

D. 6,755m

Hướng dẫn giải:

Ta có chiều cao cột đèn chính là độ dài đoạn thẳng AC trong hình với AB = 7,5m và 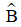= 42^o.

Xét tam giác ABC vuông tại A có:

AC = AB.tan = 7,5.tan42^o ≈ 6,753 (m)