Cách xác định điểm thuộc đường thẳng, điểm không thuộc đường thẳng cực hay, có đáp án | Toán lớp 9

Cách xác định điểm thuộc đường thẳng, điểm không thuộc đường thẳng cực hay, có đáp án

Với Cách xác định điểm thuộc đường thẳng, điểm không thuộc đường thẳng cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định điểm thuộc đường thẳng, điểm không thuộc đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Phương pháp giải

    Cho điểm M(x₀; y₀ ) và đường thẳng (d) có phương trình:

    y = ax + b. Khi đó:

    M ∈ (d) ⇔ y₀ = ax₀ + b;

    M ∉ (d) ⇔ y₀ ≠ ax₀ + b.

Ví dụ minh họa

Ví dụ 1: Cho hàm số y = (2m - 1)x + m + 1 với m ≠ 1/2. Hãy xác định m trong mỗi trường hợp sau:

    a) Đồ thị hàm số đi qua M(-1; 1)

    b) Đồ thị hàm số không đi qua điểm N (1; 3)

Hướng dẫn:

    a) Đồ thị đi qua điểm M (-1; 1) nên

    1 = (2m - 1)(-1) + m + 1 ⇔ m = 1

    Vậy với m = 1 thì đồ thị hàm số đi qua điểm M (-1; 1).

    b) Đồ thị hàm số không đi qua điểm N (1; 3) nên:

    3 ≠ (2m - 1).1 + m + 1 ⇔ 3m ≠ 3 ⇔ m ≠ 1.

Ví dụ 2: Cho đường thẳng (d): y = -2x + 3. Tìm m để đường thẳng (d) đi qua điểm A (-m; -3).

Hướng dẫn:

    Đường thẳng (d): y = -2x + 3 đi qua điểm A (-m; -3) khi:

    -3 = -2.(-m) + 3 ⇔ 2m = -6 ⇔ m = -3.

    Vậy đường thẳng (d): y = -2x + 3 đi qua điểm A (-m; -3) khi m = -3.

Ví dụ 3: Chứng minh rằng đường thẳng (d): (m + 2)x + y + 4m - 3 = 0 luôn đi qua một điểm cố định với mọi giá trị của m.

Hướng dẫn:

    Gọi điểm M(x₀; y₀ ) là điểm cố định mà (d) luôn đi qua, ta có:

    (m + 2) x₀ + y₀ + 4m - 3 = 0

    ⇔ m(x₀ + 4) + (2x₀ + y₀ - 3) = 0

    Đường thẳng (d) luôn đi qua M(x₀; y₀ ) với mọi m khi và chỉ khi:

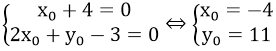
    Vậy điểm cố định mà (d) luôn qua với mọi giá trị của m là M (-4; 11).

Bài tập vận dụng

Bài 1: Cho đường thẳng (d): y = -3x + 1. Trong các điểm M(-1; 2), N(0; -1), P(1/3; 0), hãy xác định các điểm thuộc và không thuộc đường thẳng (d).

Bài 2: Cho đường thẳng (d): y = (m + 2)x + 3m - 1. Tìm m để đường thẳng (d) đi qua điểm M (-2; 3).

Hướng dẫn giải và đáp án

Hướng dẫn:

Bài 1:

    M(-1; 2) ∉ (d) vì khi x = -1 thì -3.(-1) + 1 = 4 ≠ 2

    N(0;1) ∈ (d) vì khi x = 0 thì -3.0 + 1 = 1

    P(1/3;0) ∈ (d) vì khi x = 1/3 thì (-3).1/3 + 1 = 0.

Bài 2:

    M(-2; 3) ∈ (d): y = (m + 2)x + 3m - 1 khi:

    3 = (m + 2).(-2) + 3m - 1 ⇔ 3 = -2m - 4 + 3m - 1

    ⇔ m = 8.

    Vậy đường thẳng (d): y = (m + 2)x + 3m - 1 đi qua điểm M khi m = 8.