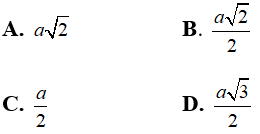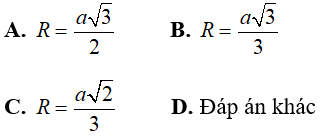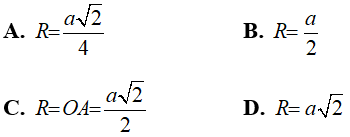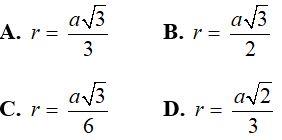Bài tập Đường tròn ngoại tiếp. Đường tròn nội tiếp chọn lọc, có đáp án | Toán lớp 9
Bài tập Đường tròn ngoại tiếp. Đường tròn nội tiếp chọn lọc, có đáp án
Với Bài tập Đường tròn ngoại tiếp. Đường tròn nội tiếp chọn lọc, có đáp án Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường tròn ngoại tiếp. Đường tròn nội tiếp từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Đường tròn ngoại tiếp đa giác là đường tròn
A. Tiếp xúc với tất cả các cạnh của đa giác đó
B. Đi qua tất cả các đỉnh của đa giác đó
C. Cắt tất cả các cạnh của đa giác đó
D. Đi qua tâm đa giác đó
Lời giải:
Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp của đa giác
Chọn đáp án B
Câu 2: Số đường tròn nội tiếp của một đa giác đều là
A. 1
B. 2
C. 3
D. 0
Lời giải:
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp
Chọn đáp án A
Câu 3: Đường tròn nội tiếp hình vuông cạnh a có bán kính là
Lời giải:
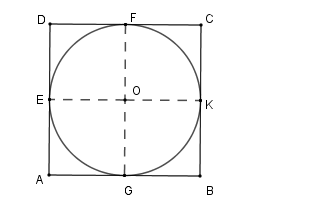

Chọn đáp án C
Câu 4: Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O. Tính số đo góc AOB
A. 60°
B. 120°
C. 30°
D. 240°
Lời giải:
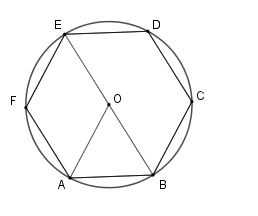
Ta có :
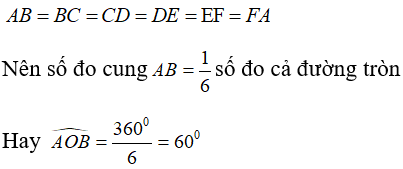
Chọn đáp án A
Câu 5: Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính R của đường tròn
Lời giải:
Do O là tâm của đường tròn ngoại tiếp tam giác đều ABC nên O đồng thời là trọng tâm tam giác AB
C.
Gọi M là trung điểm BC:

Chọn đáp án B.

Câu 6: Cho hình vuông ABCD cạnh a.Gọi O là tâm đường tròn ngoại tiếp hình vuông. Tính bán kính R của (O)?
Lời giải:
Gọi O là tâm của hình vuông ABCD
Khi đó, bán kính đường tròn ngoại tiếp hình vuông ABCD là R = OA
Áp dụng đinh lí Pytago vào tam giác vuông ABC ta có:

Chọn đáp án C.
Câu 7: Cho ngũ giác đều ABCDE nội tiếp đường tròn (O). Tính số đo AB⌢
A. 72°
B.60°
C. 120°
D. 90°
Lời giải:
Do ABCDE là ngũ giác đều nội tiếp đường tròn (O) nên:
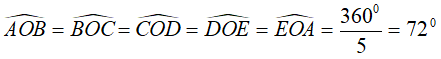
Suy ra, sđ AB⌢ = 72°
Chọn đáp án A.
Câu 8: Cho đường tròn (O) ngoại tiếp lục giác đều ABCDEF. Tính 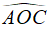
A. 120°
B.60°
C. 90°
D. 150°
Lời giải:
Ta có, đường tròn (O) ngoại tiếp lục giác đều ABCDEF nên
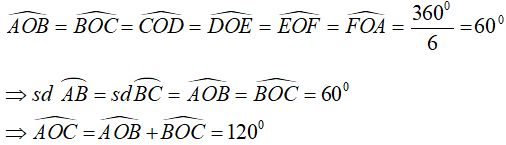
Chọn đáp án A.
Câu 9: Cho tam giác ABC đều cạnh a ngoại tiếp đường tròn tâm O. Tính bán kính đường tròn nội tiếp tam giác ABC?
Lời giải:
Gọi M là trung điểm của BC: 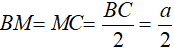
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:
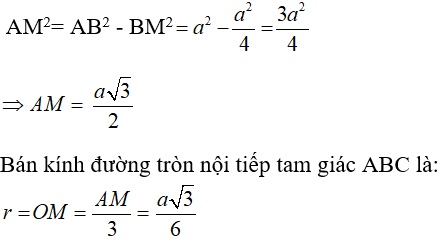
Chọn đáp án C.
Câu 10: Cho tam giác ABC có AB = 6cm; BC= 10 cm và AC = 8cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC?
A. 4cm
B. 5cm
C. 6cm
D. 7cm
Lời giải:
Ta có: AB2 + AC2 = BC2 ( = 100)
Suy ra tam giác ABC vuông tại A.
Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm cạnh huyền BC.
Đường kính đường tròn là : d = BC = 10cm
Suy ra, bán kính đường tròn ngoại tiếp tam giác ABC là R = d/2 = 5cm
Chọn đáp án B.