Các dạng bài tập Toán 9 Chương 2 phần Đại số cực hay có đáp án | Toán lớp 9

Các dạng bài tập Toán 9 Chương 2 phần Đại số cực hay có đáp án

Với Các dạng bài tập Toán 9 Chương 2 phần Đại số cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 2 phần Đại số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Các dạng bài tập Toán 9 Chương 2 phần Đại số cực hay có đáp án

I. Các dạng bài tập

II. Lý thuyết & Trắc nghiệm theo bài học

Lý thuyết hàm số bậc nhất đầy đủ nhất

1. Định nghĩa

- Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số thực cho trước và a ≠ 0

- Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x

2. Tính chất

a) Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R

b) Trên tập hợp số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) < f(x₂ )

Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) > f(x₂ )

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0)

a) Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0; nằm ở góc phần tư thứ II và thứ IV khi a < 0

b) Đồ thị của hàm số y = ax + b là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0.

Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn gọi là đường thẳng y = ax + b; b được gọi là tung độ gốc của đường thẳng.

4. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

a) Cách vẽ đồ thị của hàm số y = ax (a ≠ 0)

Cho x = 1 thì y = a. Vẽ điểm A (1; a)

Đồ thị là đường thẳng OA.

b) Cách vẽ đồ thị của hàm số y = ax + b (a ≠ 0 ; b ≠ 0)

Xác định giao điểm của đồ thị với trục tung và trục hoành

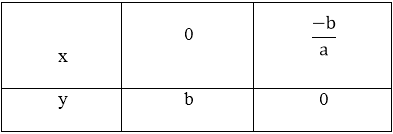
Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

P(0; b); Q((-b)/ a; 0)

Đồ thị là đường thẳng PQ

5. Chú ý

Cho hàm số y = f(x)

- Nếu tọa độ (x₀; y₀ ) của điểm A thỏa mãn hàm số y = f(x) thì điểm A thuộc đồ thị của hàm số này.

- Ngược lại, nếu điểm A (x₀; y₀ ) nằm trên đồ thị của hàm số y = f(x) thì tọa độ (x₀; y₀ ) của A thỏa mãn hàm số y = f(x)

6. Bổ sung

Trong mặt phẳng tọa độ, cho hai điểm A(x₁; y₁ ); B(x₂; y₂ ). Ta có:

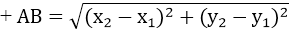
+ M (x; y) là trung điểm của AB

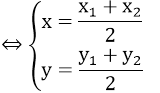
A đối xứng với B qua trục hoành ⇔ x₁ = x₂ và y₁ = -y₂ ;

A đối xứng với B qua trục tung ⇔ x₁ = -x₂ và y₁ = y₂;

A đối xứng với B qua gốc O ⇔ x₁ = -x₂ và y₁ = -y₂;

A đối xứng với B qua đường thẳng y = x ⇔ x₁ = y₂ và y₁ = x₂;

A đối xứng với B qua đường thẳng y = -x ⇔ x₁ = -y₂ và y₁ = -x₂;

Lý thuyết đường thẳng song song và đường thẳng cắt nhau đầy đủ nhất

1. Cho hai đường thẳng (d₁ ): y = ax + b (a ≠ 0)

(d₂ ): y =a'x + b' (a' ≠ 0)

+ (d₁ ) // (d₂ ) ⇔ a = a'; b ≠ b'

+ (d₁ ) ≡ (d₂ ) ⇔ a = a'; b = b'

+ (d₁ ) cắt (d₂ ) ⇔ a ≠ a'

2. Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn;

Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù.

3. Bổ sung

Cho hai đường thẳng (d₁ ): y = ax + b (a ≠ 0)

(d₂ ): y = a'x + b' (a' ≠ 0)

+ (d₁ ) ⊥ (d₂ ) ⇔ a.a' = 1

+ Nếu (d₁ ) cắt (d₂ ) thì hoành độ giao điểm là nghiệm của phương trình

ax + b = a'x + b' (gọi là phương trình hoành độ giao điểm)

+ Góc α là góc tạo bởi đường thẳng y = ax + b và trục Ox. Nếu a > 0 thì

tanα = a

Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 9

Các dạng bài tập Toán 9 Chương 2 phần Đại số cực hay có đáp án | Toán lớp 9