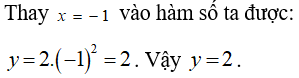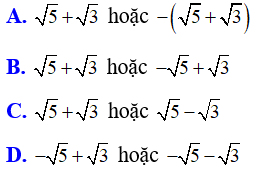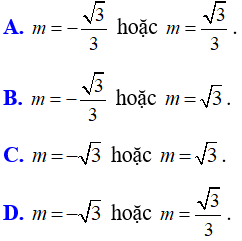Tính giá trị của hàm số tại một điểm cho trước cực hay, có đáp án | Toán lớp 9

Tính giá trị của hàm số tại một điểm cho trước cực hay, có đáp án

Với Tính giá trị của hàm số tại một điểm cho trước cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính giá trị của hàm số tại một điểm cho trước từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Bước 1: Thay giá trị của biến đã biết vào hàm số y = ax² (a ≠ 0) để tính giá trị của biến còn lại.

+) Điểm A(x₀; y₀) thuộc đồ thị hàm số y = ax² (a ≠ 0) ⇒ tọa độ điểm A thỏa mãn hàm số

y₀ = ax₀²

Bước 2: Kết luận.

B. Các ví dụ điển hình

Ví dụ 1:Điểm A(3; y₀) thuộc đồ thị hàm số 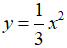. Giá trị y₀ bằng:

Lời giải

Chọn B

Ví dụ 2: Một vật rơi tự do ở độ cao so với mặt đất 400(m). Quãng đường chuyển động s (m) của vật rơi tự do phụ thuộc vào thời gian t (giây) theo công thức s = 4t² . Hỏi sau bao lâu thì vật này tiếp đất?

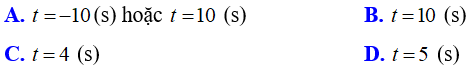
Lời giải

Chọn B

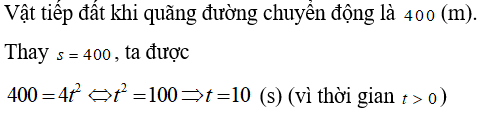
Ví dụ 3: Điểm nào sau đây không thuộc đồ thị hàm số ?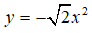

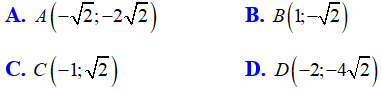
Lời giải

Chọn C

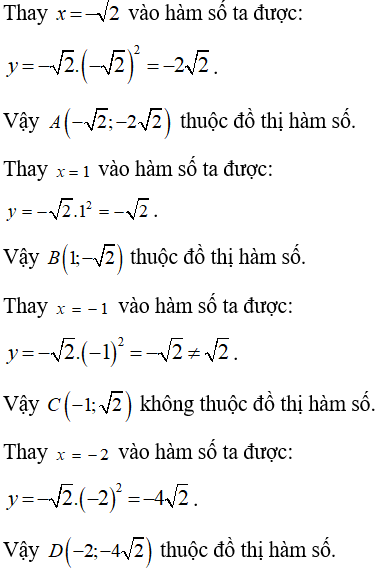
C. Bài tập vận dụng

Bài 1: Giá trị của hàm số y = 2x² tại x = -1 là:

Lời giải:

Đáp án C

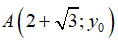
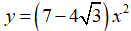
Bài 2: Điểm thuộc đồ thị hàm số . Tung độ của điểm A là:

Lời giải:

Đáp án A

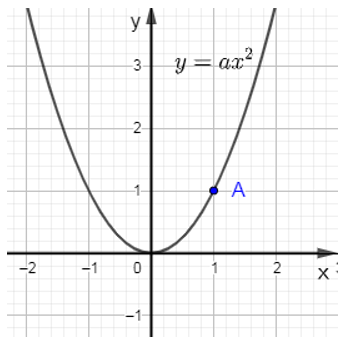
Bài 3: Cho hàm số y = ax² (a ≠ 0) có một phần đồ thị như hình vẽ sau đây:

Giá trị của hàm số tại x = 2 là:

Lời giải:

Đáp án A

Bài 4: Đồ thị của hàm số y = (m² + 1)x² (với m là tham số) đi qua điểm E(2; 5). Giá trị của hàm số tại 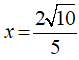là:

Lời giải:

Đáp án B

Bài 5: Điểm B có hoành độ bằng -2 thuộc đồ thị hàm số 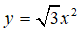. Tung độ của điểm B là:

Lời giải:

Đáp án A

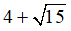
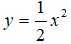
Bài 6: Điểm C có tung độ thuộc đồ thị hàm số . Hoành độ của điểm C là:

Lời giải:

Đáp án

Bài 7: Một bể nước hình hộp chữ nhật có đáy là hình vuông cạnh x (m) và chiều cao của bể là 2 (m). Gọi V (m³) là thể tích của bể. Khi đáy bể là hình vuông cạnh 3(m) thì bể đó có thể chứa đầy bao nhiêu mét khối nước?

Lời giải:

Đáp án A

Bài 8: Cho hàm số y = -2x² và các khẳng định sau:

1. Điểm 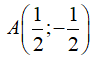thuộc đồ thị hàm số.

2. Khi y = -8 thì x = 2.

3. Hàm số trên không có giá trị dương.

4. Đồ thị hàm số số có điểm thấp nhất.

Số khẳng định đúng là:

Lời giải:

Đáp án A

Bài 9: Cho hàm số y = ax²(a ≠ 0) có đồ thị đi qua điểm A(3; 3). Giá trị của m để điểm B(m; 1) cũng thuộc đồ thị hàm số trên là:

Lời giải:

Đáp án C

Bài 10: Điểm C(m; n) thuộc đồ thị hàm số y = ax²(a ≠ 0). Điểm nào sau đây cũng thuộc đồ thị hàm số trên?

Lời giải:

Đáp án D