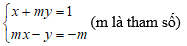Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay | Toán lớp 9

Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay

Với Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Phương pháp:

Bước 1: Tìm điều kiện của m để hệ có nghiệm duy nhất sau đó giải hệ phương trình tìm nghiệm (x;y) theo tham số m.

Bước 2: Thế x và y vừa tìm được vào biểu thức điều kiện, sau đó giải tìm m.

Bước 3: Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Cho hệ phương trình 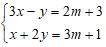(m là tham số).

Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn x² + y² = 5.

Hướng dẫn:

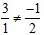
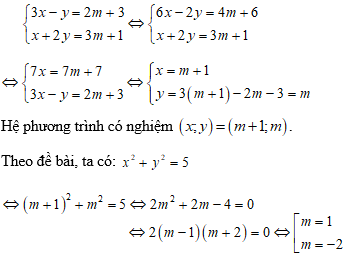
Vì nên hệ phương trình luôn có nghiệm duy nhất (x;y).

Vậy m = 1 hoặc m = –2 thì phương trình có nghiệm thỏa mãn đề bài.

Ví dụ 2: Cho hệ phương trình 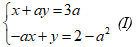(a là tham số).

Tìm a để hệ phương trình có nghiệm duy nhất 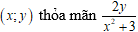là số nguyên.

Hướng dẫn:

Hệ phương trình luôn có nghiệm duy nhất (x;y) = (a;2).

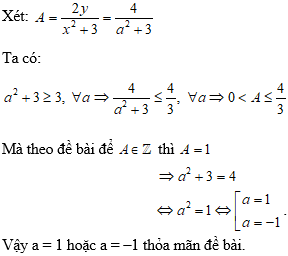
Ví dụ 3: Cho hệ phương trình: 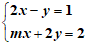(I) (m là tham số).

Tìm m đề hệ phương trình có nghiệm duy nhất sao cho 2x – 3y = 1.

Hướng dẫn:

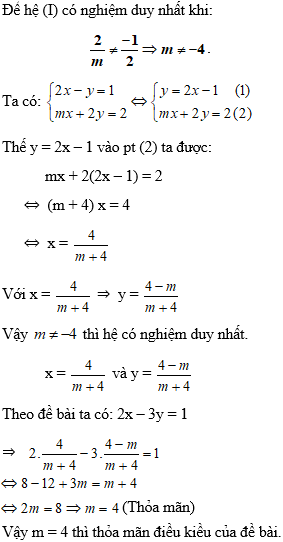
C. Bài tập trắc nghiệm

Sử dụng hệ sau trả lời câu 1, câu 2, câu 3.

Cho hệ phương trình sau (I):

Câu 1: Với giá trị nào của m thì hệ có nghiệm duy nhất thỏa mãn x = y + 1.

 A. m = 0

 B. m = 1

 C. m = 0 hoặc m = –1

 D. m = 0 hoặc m = 1

Lời giải:

Hướng dẫn:

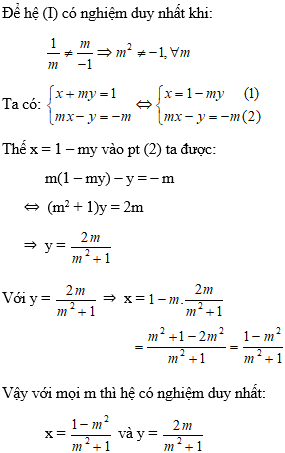
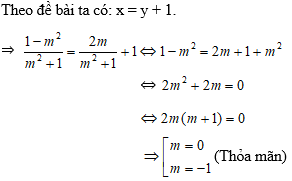
Vậy với m = 0 hoặc m = –1 thỏa mãn điều kiện đề bài.

Chọn đáp án C.

Câu 2: Với giá trị nào của m thì hệ có nghiệm duy nhất thỏa mãn x < 0, y > 0.

 A. m > 0

 B. m < 0

 C. m < 1

 D. m > 1

Lời giải:

Hướng dẫn:

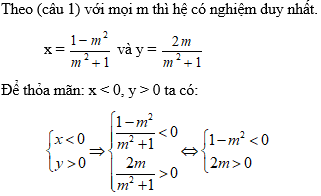
• 1 – m² < 0 ⇒ (1 – m)(1 + m) < 0 ⇒ m < –1 hoặc m > 1.(*)

• 2m > 0 ⇒ m > 0.(**)

Kết hợp điều kiện hai trương hợp trên, suy ra m > 1.

Vậy m > 1 thì thỏa mãn x < 0, y> 0.

Chọn đáp án D.

Câu 3: Với giá trị nào của m thì hệ có nghiệm duy nhất thỏa mãn x < 1.

 A. m > 0

 B. với mọi m khác 0

 C. không có giá trị của m

 D. m < 1

Lời giải:

Hướng dẫn:

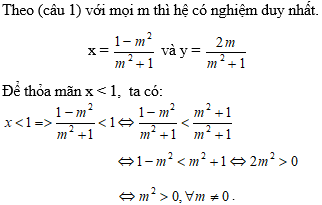
Vậy với mọi m khác 0 thì thỏa mãn điều kiện đề bài: x < 1.

Chọn đáp án B.

Sử dụng hệ sau trả lời câu 4, câu 5.

Cho hệ phương trình: 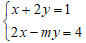.(m là tham số).

Câu 4: Với giá trị nào của m để hệ có nghiệm duy nhất sao cho x – 1 > 0. Khẳng định nào sau đây là đúng ?

 A. với mọi m thì hệ có nghiệm duy nhất.

 B. với m > 2 thì hệ có nghiệm thỏa mãn x – 1 > 0.

 C. với m > –2 thì hệ có nghiệm thỏa mãn x – 1 > 0.

 D. Cả A, B, C đều sai.

Lời giải:

Hướng dẫn:

Để hệ phương trình có nghiệm duy nhất .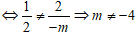

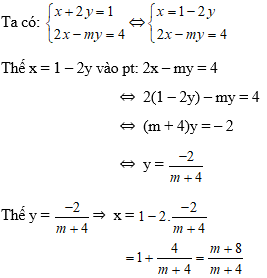
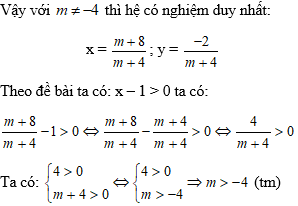
Vậy m > – 4 thì thỏa mãn điều kiện x – 1 > 0.

Chọn đáp án D.

Câu 5: Với giá trị nào của m để hệ có nghiệm duy nhất sao cho 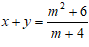. Khẳng định nào sau đây là đúng ?

 A. với m = 0 hoặc m = 1 thì hệ thỏa mãn điều kiện bài toán.

 B. với m = 0 thì hệ thỏa mãn điều kiện bài toán.

 C. với m = 1 thì hệ thỏa mãn điều kiện bài toán.

 D. Cả A, B, C đều đúng.

Lời giải:

Hướng dẫn:

Chọn đáp án A.

Sử dụng hệ sau trả lời câu 6.

Cho hệ phương trình: 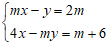.(m là tham số).

Câu 6: Với giá trị nào của m để hệ có nghiệm duy nhất sao cho 3x – y = 5.

 A. m = 2,

 B. m = – 2

 C. m = 0,5

 D. m = - 0,5

Lời giải:

Hướng dẫn:

Để hệ phương trình có nghiệm duy nhất:

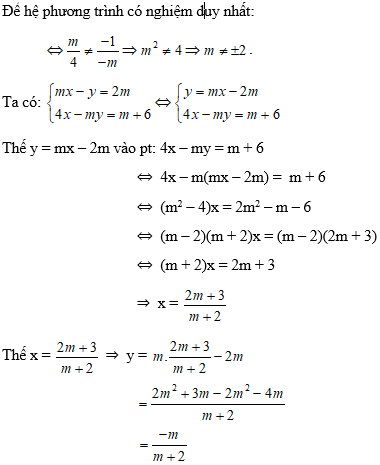
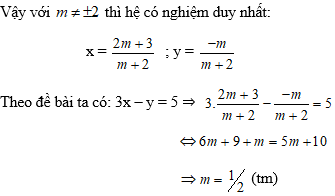
Vậy với m = ½ thỏa mãn điều kiện đề bài.

Chọn đáp án C.

Câu 7: Cho hệ phương trình: 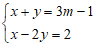.(m là tham số).

Với giá trị nào của m để hệ có nghiệm duy nhất sao cho x² – 2y² = –2.

 A. m = 0

 B. m = 2

 C. m = 0 hoặc m = –2

 D. m = 0 hoặc m = 2

Lời giải:

Hướng dẫn:

Trừ vế theo vế của pt (1) với pt (2) ta được: 3y = 3m – 3 ⇔ y = m - 1

Thế y = m - 1 vào pt: x – 2y = 2 ⇔ x – 2(m – 1) = 2 ⇔ x = 2m

Vậy hệ phương trình có nghiệm là: x = 2m; y = m – 1

Theo đề bài ta có: x² – 2y² = –2 ⇒ (2m)² – 2 (m – 1)² = –2

⇔ 4m² – 2m² + 4m – 2 = –2 ⇔ m² + 2m = 0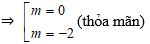

Vậy với m = 0 hoặc m = –2 thì hệ thỏa mãn điều kiện: x² – 2y² = –2.

Chọn đáp án C.

Câu 8: Cho hệ phương trình: 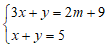. (m là tham số), có nghiệm (x;y). Với giá trị nào của m để A = xy + x – 1 đạt giá trị lớn nhất.

 A. m = 1

 B. m = 2

 C. m = –1

 D. m = 3

Lời giải:

Hướng dẫn:

Trừ vế theo vế của pt (1) với pt (2) ta được: 2x = 2m + 4 ⇔ x = m + 2

Thế x = m + 2 vào pt: x + y = 5 ⇔ m + 2 + y = 5 ⇔ y = 3 – m

Vậy hệ phương trình có nghiệm là: x = m + 2; y = 3 – m

Theo đề bài ta có:

A = xy + x – 1

= (m + 2)(3 – m) + m + 2 – 1

= – m² + 2m – 1 + 8

= 8 – (m – 1)² 8

Vậy A_max = 8 ⇔ m = 1

Vậy với m = 1 thì A đạt giá trị lớn nhất.

Chọn đáp án A.

Câu 9: Cho hệ phương trình: 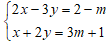. (m là tham số), có nghiệm (x;y). Tìm m nguyên để T = y/x nguyên.

 A. m = 1

 B. m = –2 hoặc m = 0

 C. m = -2 và m = 1

 D. m = 3

Lời giải:

Hướng dẫn:

Để T nguyên thì (m + 1) là ước của 1.⇒ (m + 1)

• m + 1 = –1 ⇒ m = –2.

• m + 1 = 1 ⇒ m = 0.

Vậy với m = –2 hoặc m = 0 thì T nguyên.

Chọn đáp án B.

Câu 10: Tìm số nguyên m để hệ phương trình: 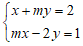. (m là tham số), có nghiệm (x;y) thỏa mãn x > 0, y < 0.

 A. m ∈ Z

 B. m ∈ {-3;-2;-1;0}

 C. vô số.

 D. không có

Lời giải:

Hướng dẫn:

hệ phương trình có nghiệm duy nhất:

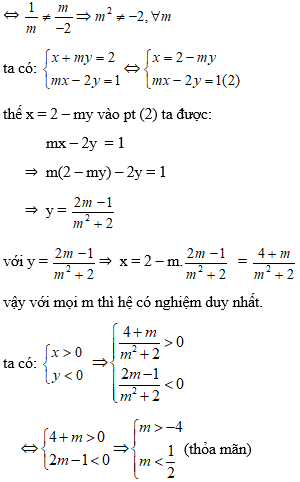
vậy m ∈ {-3;-2;-1;0} thì hệ thỏa mãn x > 0, y < 0.

Chọn đáp án B.