Bài tập trắc nghiệm Chương 2 Hình học 9 chọn lọc, có đáp án | Toán lớp 9

Bài tập trắc nghiệm Chương 2 Hình học 9 chọn lọc, có đáp án

Với Bài tập trắc nghiệm Chương 2 Hình học 9 chọn lọc, có đáp án Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 2 Hình học từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Số tâm đối xứng của đường tròn là

A. 1

B. 2

C. 3

D. 4

Lời giải:

Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.

Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn

Chọn đáp án A

Câu 2: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn

A. Đường tròn không có trục đối xứng

B. Đường tròn có duy nhất một trục đối xứng là đường kính

C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau

D. Đường tròn có vô số trục đối xứng là đường kính

Lời giải:

Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn

Nên đường tròn có vô số trục đối xứng

Chọn đáp án D

Câu 3: Tâm của đường tròn ngoại tiếp tam giác là

A. Giao của ba đường phân giác

B. Giao của ba đường trung trực

C. Giao của ba đường cao

D. Giao của ba đường trung tuyến

Lời giải:

Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó

Chọn đáp án B

Câu 4: Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?

A. Điểm M nằm ngoài đường tròn

B. Điểm M nằm trên đường tròn

C.Điểm M nằm trong đường tròn

D. Điểm M không thuộc đường tròn

Lời giải:

Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:

Chọn đáp án B

Câu 5: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a

A. Tâm là giao điểm A và bán kính R = a√2

B. Tâm là giao điểm hai đường chéo và bán kính R = a√2

C. Tâm là giao điểm hai đường chéo và bán kính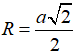

D. Tâm là điểm B và bán kính là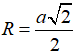

Lời giải:

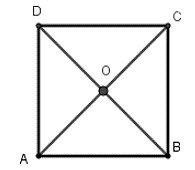
Gọi O là giao hai đường chéo của hình vuông ABCD.

Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2

Xét tam giác vuông tại ta có:

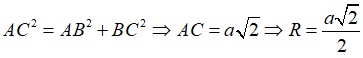
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là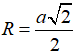

Chọn đáp án C

Câu 6: Tâm của đường tròn ngoại tiếp tam giác vuông là

A. Trung điểm cạnh huyền

B. Trung điểm cạnh góc vuông lớn hơn

C. Giao ba đường cao

D. Giao ba đường trung tuyến

Lời giải:

Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp

Chọn đáp án A

Câu 7: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó

A. Tâm là trọng tâm tam giác ABC và bán kính R = 2/3 AI với I là trung điểm của

B. Tâm là trung điểm AB và bán kính R = AB/2

C.Tâm là giao điểm của BD và EC, bán kính là R = AB/2

D. Tâm là trung điểm BC và bán kính là R = BC/2

Lời giải:

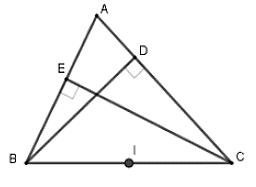
Chọn đáp án D

Câu 8: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A(-1; -1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2

A. Điểm A nằm ngoài đường tròn

B. Điểm A nằm trên đường tròn

C. Điểm A nằm trong đường tròn

D. Không kết luận được

Lời giải:

Ta có: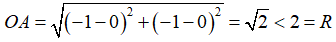

Nên A nằm trong đường tròn tâm O bán kính R = 2

Chọn đáp án C

Câu 9: Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC

A. R = 25

B. R = 25/2

C. R = 15

D. R = 20

Lời giải:

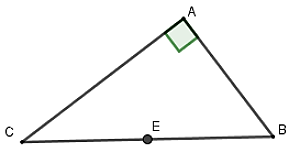
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = BC/2

Theo định lý Pytago ta có 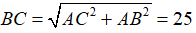nên bán kính R = 25/2

Chọn đáp án B

Câu 10: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D

A. R = 7,5cm

B. R = 13cm

C. R = 6cm

D. R = 6,5cm

Lời giải:

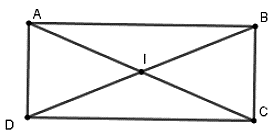
Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm mỗi đường)

Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = AC/2

Theo định lý Pytago trong tam giác vuông ABC

Ta có:

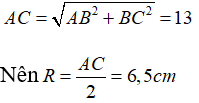
Vậy bán kính cần tìm là R = 6,5cm

Chọn đáp án D

Câu 11: Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?

A. AB > CD

B. AB = CD

C. AB < CD

D. AB ≤ CD

Lời giải:

Trong các dây của đường tròn, dây lớn nhất là đường kính

Chọn đáp án A.

Câu 12: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng

A. AB > CD

B. AB = CD

C. AB < CD

D. AB // CD

Lời giải:

Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau

Chọn đáp án B.

Câu 13: “Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp

A. nhỏ hơn

B. bằng

C. song song

D. vuông góc

Lời giải:

Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy

Chọn đáp án D.

Câu 14: Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn

A. Dây nào lớn hơn thì dây đó xa tâm hơn

B. Dây nào nhỏ hơn thì đây đó xa tâm hơn

C. Dây nào gần tâm hơn thì dây đó lớn hơn

D. Hai dây bằng nhau thì cách đều tâm

Lời giải:

Trong một đường tròn:

+ Hai dây bằng nhau thì cách đều tâm

- Trong hai dây của đường tròn:

+ Dây nào lớn hơn thì dây đó gần tâm hơn

+ Dây nào gần tâm hơn thì dây đó lớn hơn

Nên phương án B, C, D đúng

Chọn đáp án A.

Câu 15: Cho đường tròn (O) có bán kính R = 5 cm. Khoảng cách từ tâm đến dây AB là 3 cm. Tính độ dài dây AB

A. AB = 6 cm

B. AB = 8 cm

C. AB = 10 cm

D. AB = 12 cm

Lời giải:

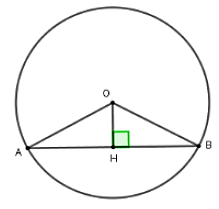
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB

Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:

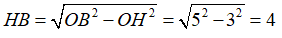
Mà H là trung điểm của AB nên AB = 2HB = 8 cm

Vậy AB = 8 cm

Chọn đáp án B.

Câu 16: Cho đường tròn (O; R = 25). Khi đó dây cung lớn nhất của đường tròn đó bằng?

A. 12,5

B. 25

C. 50

D. 20

Lời giải:

Trong đường tròn thì đường kính là dây lớn nhất của đường tròn đó

Vậy dây lớn nhất của đường tròn là 2R = 2.25 = 50

Chọn đáp án C.

Câu 17: Cho đường tròn (O; R = 20). Cho dây cung MN có độ dài 36. Khoảng cách từ tâm O đến dây cung là?

A. 15

B. √35

C. √76

D. 20

Lời giải:

Khoảng cách từ O đến dây cung MN là:

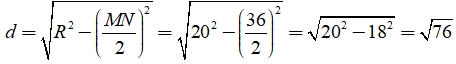
Chọn đáp án C.

Câu 18: Cho đường tròn (O; R), có dây cung MN có độ dài là 24cm, khoảng cách từ O đến đường thẳng MN là 16cm. Độ dài bán kính R là?

A. 24cm

B. 25cm

C. 16cm

D. 20cm

Lời giải:

Độ dài bán kính của đường tròn là:

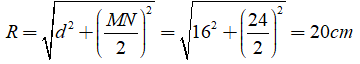
Chọn đáp án D.

Câu 19: Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung

A. 1

B. 2

C.3

D. 4

Lời giải:

Đường thẳng và đường tròn có nhiều nhất hai điểm chung

Chọn đáp án B

Câu 20: Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì

A. đường thẳng tiếp xúc với đường tròn

B. đường thẳng cắt đường tròn

C. đường thẳng không cắt đường tròn

D. đáp án khác

Lời giải:

Đường thẳng và đường tròn chỉ có một điểm chung thì đường thẳng tiếp xúc với đường tròn

Chọn đáp án A

Câu 21: Nếu đường thẳng d là tiếp tuyến của đường tròn (O) tại A thì

A. d // OA

B. d ≡ OA

C. d ⊥ OA tại A

D. d ⊥ OA tại O

Lời giải:

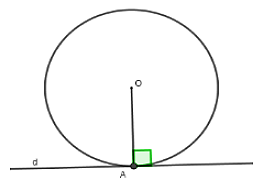
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm

Nên d ⊥ OA tại tiếp điểm A

Chọn đáp án C

Câu 22: Cho đường tròn (O) và đường thẳng a. Kẻ OH ⊥ a tại H, biết OH > R khi đó đường thẳng a và đường tròn (O)

A. cắt nhau

B. không cắt nhau

C. tiếp xúc

D. đáp án khác

Lời giải:

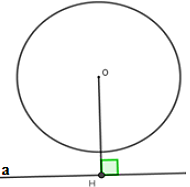
Vì OH > R nên α không cắt (O)

Chọn đáp án B

Câu 23: Điền vào các vị trí (1); (2) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):

A. (1): cắt nhau; (2): 8cm

B. (1): 9cm ; (2): cắt nhau

C. (1): không cắt nhau; (2): 8cm

D. (1): cắt nhau; (2): 6cm

Lời giải:

+ Vì d < R (4cm < 5cm) nên đường thẳng cắt đường tròn

+ Vì đường thẳng tiếp xúc với đường tròn nên d = R = 8cm

Chọn đáp án A

Câu 24: Cho (O; R).Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi

A. d ⊥ OA tại A và A ∈ (O)

B. d ⊥ OA

C. A ∈ (O)

D. d // OA

Lời giải:

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn

Chọn đáp án A

Câu 25: Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó

A. Khoảng cách từ O đến đường thẳng d nhỏ hơn 5cm

B. Khoảng cách từ O đến đường thẳng d lớn hơn 5cm

C. Khoảng cách từ O đến đường thẳng d bằng 5cm

D. Khoảng cách từ đến O đường thẳng d bằng 6cm

Lời giải:

Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó

Chọn đáp án C

Câu 26: Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?

A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm

B.AB là cát tuyến của đường tròn (C; CA)

C.AB là tiếp tuyến của (C; CA)

D. BC là tiếp tuyến của (C; CA)

Lời giải:

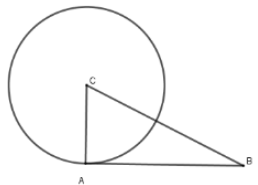
+ Xét tam giác có:

BC² = 5² = 25; AB² + AC² = 4² + 3² = 25 ⇒ BC² = AB² + AC²

⇒ ΔABC vuông tại A (Định lý Pytago đảo)

⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)

Chọn đáp án C

Câu 27: Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI

A. HK

B. IB

C. IC

D. Ac

Lời giải:

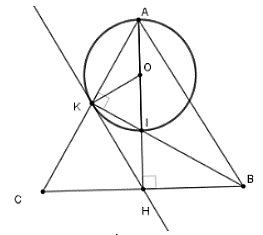
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

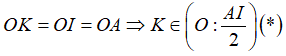
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

Chọn đáp án A

Câu 28: Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau

A. DE là cát tuyến của đường tròn đường kính BH

B. DE là tiếp tuyến của đường tròn đường kính BH

C. Tứ giác AEHD là hình chữ nhật

D. DE ⊥ DI (với I là trung điểm BH)

Lời giải:

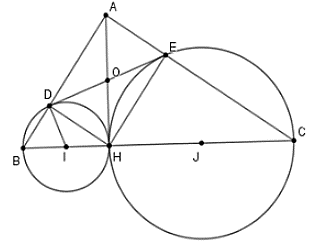
Gọi I, J lần lượt là trung điểm của BH và CH.

Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay

Vì D, E lần lượt thuộc đường tròn đường kính BH và HC

Nên DE là tiếp tuyến của đường tròn đường kính BH

Từ chứng minh trên suy ra các phương án B, C, D đúng

Chọn đáp án A

Câu 29: Tâm đường tròn nội tiếp của tam giác là

A. giao của ba đường phân giác góc trong tam giác

B. giao ba đường trung trực của tam giác

C. trọng tâm tam giác

D. trực tâm của tam giác

Lời giải:

Tâm đường tròn nội tiếp của tam giác là giao của ba đường phân giác góc trong tam giác

Chọn đáp án A

Câu 30: Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp

A. 1

B. 2

C. 3

D. 4

Lời giải:

Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp của tam giác

Với một tam giác có ba đường tròn bàng tiếp

Chọn đáp án C

Câu 31: Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?

A. Khoảng cách từ điểm đó đến hai tiếp điểm là bằng nhau

B. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai bán kính

C. Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính

D. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai tiếp tuyến

Lời giải:

Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:

+ Điểm đó cách đều hai tiếp điểm

+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến

+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm

Chọn đáp án B

Câu 32: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Vẽ đường kính CD của (O). Khi đó:

A. BD // OA

B. BD // AC

C. BD ⊥ OA

D. BD cắt OA

Lời giải:

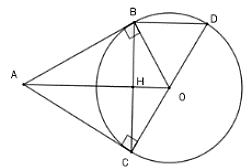
*Xét tam giác BOC có OB = OC = R nên tam giác OBC cân tại O có OH là đường phân giác của góc 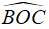( tính chất hai tiếp tuyến cắt nhau).

Do đó, OH đồng thời là đường cao: (1)

Chọn đáp án A

Câu 33: Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là:

A. 1

B. 2

C. 3

D. 4

Lời giải:

Hai đường tròn tiếp xúc với nhau thì có một điểm chung duy nhất

Chọn đáp án A

Câu 34: Cho hai đường tròn (O; R) và (O; r) với R > r cắt nhau tại hai điểm phân biệt và OO' = d . Chọn khẳng định đúng?

A. d = R - r

B. d > R + r

C. R - r < d < R + r

D. d < R - r

Lời giải:

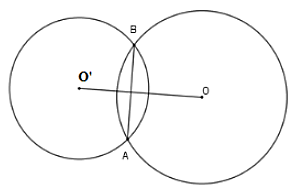
Hai đường tròn (O; R) và (O'; r)(R > r) cắt nhau

Khi đó (O) và (O') có hai điểm chung và đường tròn nối tâm là đường trung trực của đoạn AB

Hệ thức liên hệ R - r < OO' < R + r

Chọn đáp án C

Câu 35: Cho hai đường tròn (O; 8cm) và (O; 6cm) cắt nhau tại A, B sao cho OA là tiếp tuyến của (O). Độ dài dây AB là

A. AB = 8,6 cm

B. AB = 6,9 cm

C. AB = 4,8 cm

D. AB = 9,6 cm

Lời giải:

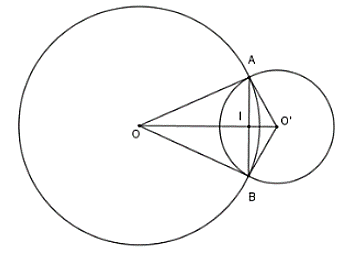
Vì OA là tiếp tuyến của (O') nên tam giác vuông tại A

Vì (O) và (O') cắt nhau tại A, B nên đường tròn nối tâm OO' là trung trực của đoạn AB

Gọi giao điểm của AB và OO' là I thì AB ⊥ OO' tại I là trung điểm của AB

Áp dụng hệ thức lượng trong tam giác vuông OAO' ta có:

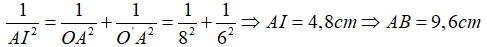
Chọn đáp án D

Câu 36: Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Vị trí tương đối của hai đường tròn là:

A. Nằm ngoài nhau

B. Cắt nhau

C. Tiếp xúc ngoài

D. Tiếp xúc trong

Lời giải:

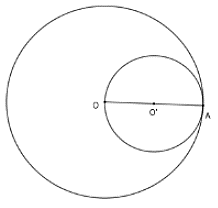
Vì hai đường tròn có một điểm chung là A và 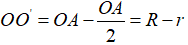nên hai đường tròn tiếp xúc trong

Chọn đáp án D

Câu 37: Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C. Khi đó

Lời giải:

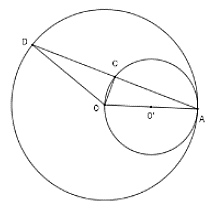
Chọn đáp án B