Cách tính diện tích tam giác bằng tỉ số lượng giác cực hay, có đáp án | Toán lớp 9

Cách tính diện tích tam giác bằng tỉ số lượng giác cực hay, có đáp án

Với Cách tính diện tích tam giác bằng tỉ số lượng giác cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính diện tích tam giác bằng tỉ số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Ví dụ minh họa

Ví dụ 1: Chứng minh rằng diện tích của một tam giác bằng nửa tích hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy

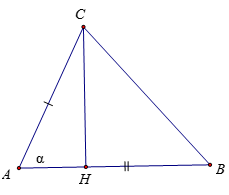
Hướng dẫn:

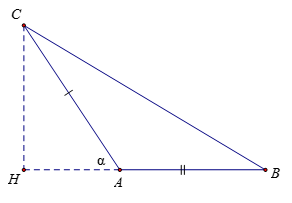
    Gọi α là số đo góc nhọn tạo bởi hai đường thẳng AB và AC của tam giác ABC. Vẽ đường cao CH

    Xét tam giác ACH vuông tại H có: CH = AC.sin⁡α

    Diện tích tam giác ABC là:

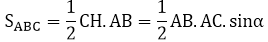
Ví dụ 2: Cho hình bình hành ABCD, AB = a, AD = b, góc D bằng α < 90⁰. Chứng minh rằng diện tích của hình bình hành được tính theo công thức S = a.b.sin⁡α

Hướng dẫn:

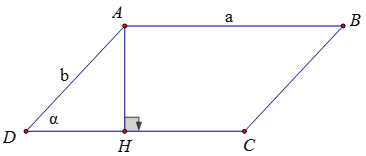
    Vẽ đường cao AH. Ta có: AH = AD.sin⁡α

    Diện tích của hình bình hành ABCD là:

    S = AB.AH = AB.AB.sin⁡α = a.b.sin⁡α

Ví dụ 3: Tứ giác ABCD có AC = m, BD = n, góc nhọn tạo bởi hai đường chéo bằng α. Chứng minh rằng diện tích của tứ giác này được tính theo công thức

    S = 1/2.m.n.sin⁡α

Hướng dẫn:

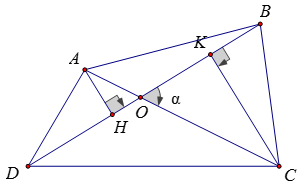
    Gọi O là giao điểm của hai đường chéo AC và BD

    Giả sử góc BOC bằng α. Vẽ AH ⊥ BD; CK ⊥ BD

    Diện tích tứ giác ABCD là:

Ví dụ 4: Cho tam giác ABC, góc A bằng 60⁰; AB + AC = 8 cm. Tính giá trị lớn nhất của diện tích tam giác ABC

Hướng dẫn:

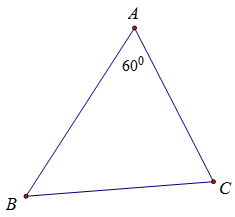
    Gọi S là diện tích của tam giác ABC. Ta có:

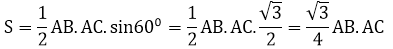
    Mặt khác:

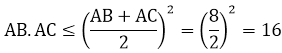
    Dấu bằng xảy ra khi AB = AC = 4 cm

    Do đó:

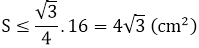
    Vậy maxS = 4√3 (cm² ) khi tam giác ABC cân tại A

    Lưu ý: Trong bài giải, ta đã sử dụng bất đẳng thức a.b ≤ ((a + b)/2)² đây chính là Bất đẳng thức Cô- si viết dưới dạng không có dấu căn.