Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn hay, chi tiết | Toán lớp 9
Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn hay, chi tiết
Tài liệu Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Góc có đỉnh ở bên trong đường tròn
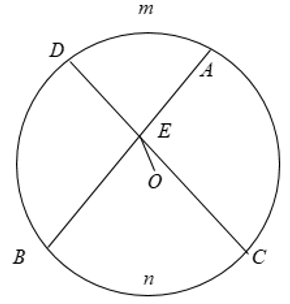
+ Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.
+ Hình vẽ: Góc ∠BEC là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là 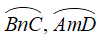
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Hay 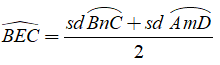
2. Góc có đỉnh nằm bên ngoài đường tròn
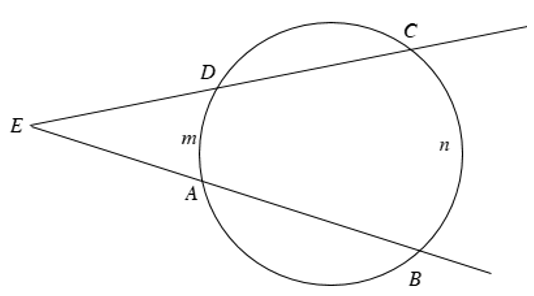
+ Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.
+ Hai cung bị chắn là hai cung nằm bên trong góc, hình vẽ trên: Góc ∠BEC là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là 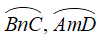
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Hay 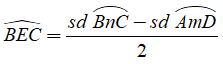

3. Ví dụ
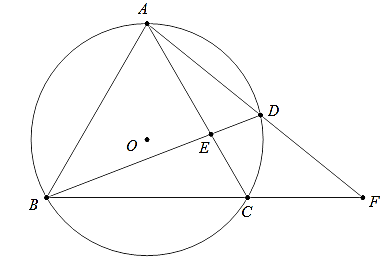
Ví dụ 1: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Điểm D di chuyển trên cung AC, E là giao điểm của AC với BD, F là giao điểm của AD và BC. Chứng minh rằng: 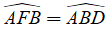
Hướng dẫn:
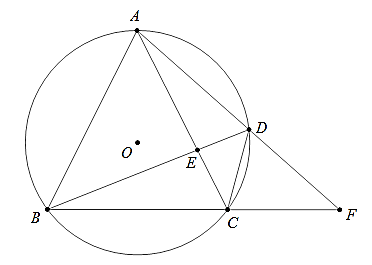
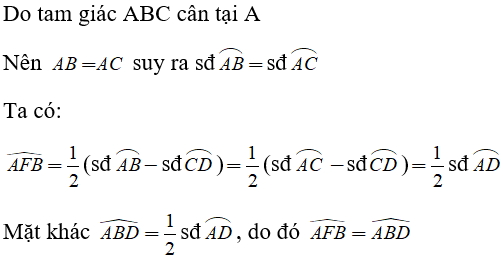
Ví dụ 2: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P, Q, R lần lượt là giao điểm của các tia phân giác trong góc A, B, C với đường tròn. Chứng minh: AP ⊥ QR
Hướng dẫn:
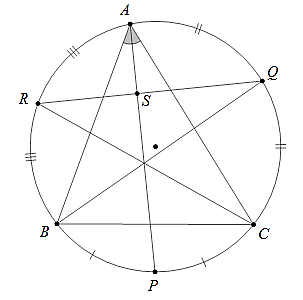
Ta có:
Tia phân giác AP chia đôi cung BC⌢ thành hai cung bằng nhau

B. Bài tập tự luận
Câu 1: Cho tam giác đều ABC nội tiếp đường tròn tâm O. D là một điểm di động trên cung nhỏ AC, gọi F là giao điểm AD và BC và E là giao điểm của AC và BD. Chứng minh tích AE.BF không phụ thuộc vào vị trị của D.
Lời giải:

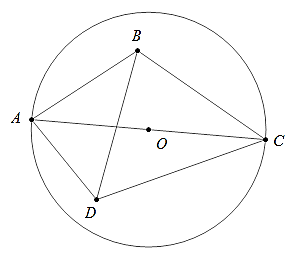
Câu 2: Tứ giác ABCD có các góc B và D tù. Chứng minh AC > BD
Lời giải: