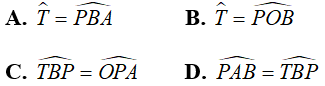Lý thuyết Góc tạo bởi tia tiếp tuyến và dây cung hay, chi tiết | Toán lớp 9
Lý thuyết Góc tạo bởi tia tiếp tuyến và dây cung hay, chi tiết
Tài liệu Lý thuyết Góc tạo bởi tia tiếp tuyến và dây cung hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Góc tạo bởi tia tiếp tuyến và dây cung từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định nghĩa
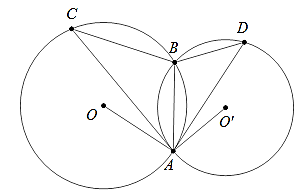
+ Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.
+ Cung nằm bên trong là cung bị chắn.
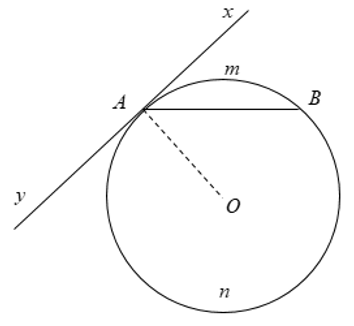
+ Hình vẽ:

2. Định lý.
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Cụ thể:
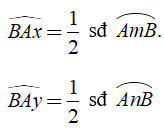
3. Hệ quả.
+ Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+ Định lý bổ sung: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn.

4. Ví dụ
Ví dụ 1: Cho đường tròn (O; R) và điểm A nằm trên đường tròn , tiếp tuyến tại A cắt đường kính BC của đường tròn tại S. Biết 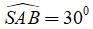
Hướng dẫn:
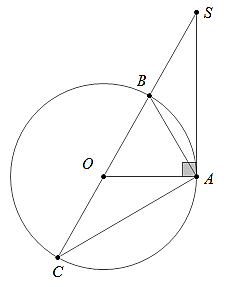
Ta có:

Ví dụ 2: Cho đường tròn (O; R) và điểm I nằm ngoài đường tròn sao cho OI = 2R. Điểm C nằm trên đường tròn, vẽ tiếp tuyến AI của đường tròn, gọi B là giao điểm của OI và (O) (B nằm giữa O và I). Tính 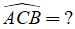
Hướng dẫn:
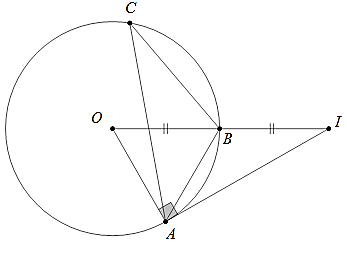
Ta có:

B. Bài tập tự luận

Câu 1: Cho đường tròn (O) và điểm M nằm ngoài đường tròn, từ M vẽ cát tuyến MAB đến đường tròn. C là điểm trên đường tròn khác A và B. Chứng minh rằng MC là tiếp tuyến của đường tròn (O) khi và chỉ khi MC2 = MA.MB .
Lời giải:

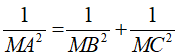
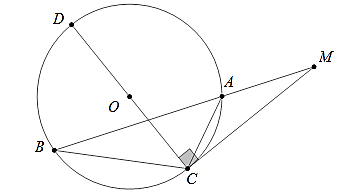
Câu 2: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.
Chứng minh AB2 = BD.BC
Lời giải: