Lý thuyết hàm số bậc nhất đầy đủ nhất | Toán lớp 9

Lý thuyết hàm số bậc nhất đầy đủ nhất

Tài liệu Lý thuyết hàm số bậc nhất đầy đủ nhất Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về hàm số bậc nhất từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định nghĩa

    - Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số thực cho trước và a ≠ 0

    - Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x

2. Tính chất

    a) Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R

    b) Trên tập hợp số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

    Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) < f(x₂ )

    Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) > f(x₂ )

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0)

    a) Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0; nằm ở góc phần tư thứ II và thứ IV khi a < 0

    b) Đồ thị của hàm số y = ax + b là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0.

    Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn gọi là đường thẳng y = ax + b; b được gọi là tung độ gốc của đường thẳng.

4. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

    a) Cách vẽ đồ thị của hàm số y = ax (a ≠ 0)

    Cho x = 1 thì y = a. Vẽ điểm A (1; a)

    Đồ thị là đường thẳng OA.

    b) Cách vẽ đồ thị của hàm số y = ax + b (a ≠ 0 ; b ≠ 0)

    Xác định giao điểm của đồ thị với trục tung và trục hoành

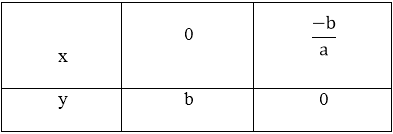
    P(0; b); Q((-b)/ a; 0)

    Đồ thị là đường thẳng PQ

5. Chú ý

    Cho hàm số y = f(x)

    - Nếu tọa độ (x₀; y₀ ) của điểm A thỏa mãn hàm số y = f(x) thì điểm A thuộc đồ thị của hàm số này.

    - Ngược lại, nếu điểm A (x₀; y₀ ) nằm trên đồ thị của hàm số y = f(x) thì tọa độ (x₀; y₀ ) của A thỏa mãn hàm số y = f(x)

6. Bổ sung

    Trong mặt phẳng tọa độ, cho hai điểm A(x₁; y₁ ); B(x₂; y₂ ). Ta có:

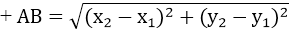
    + M (x; y) là trung điểm của AB

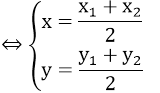
    A đối xứng với B qua trục hoành ⇔ x₁ = x₂ và y₁ = -y₂ ;

    A đối xứng với B qua trục tung ⇔ x₁ = -x₂ và y₁ = y₂;

    A đối xứng với B qua gốc O ⇔ x₁ = -x₂ và y₁ = -y₂;

    A đối xứng với B qua đường thẳng y = x ⇔ x₁ = y₂ và y₁ = x₂;

    A đối xứng với B qua đường thẳng y = -x ⇔ x₁ = -y₂ và y₁ = -x₂;