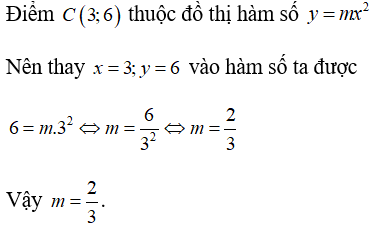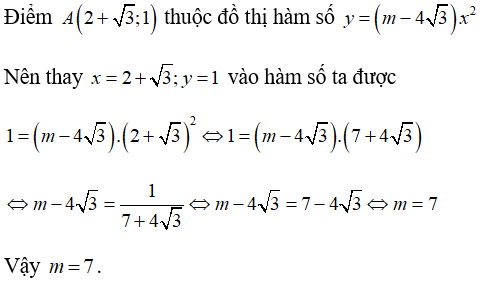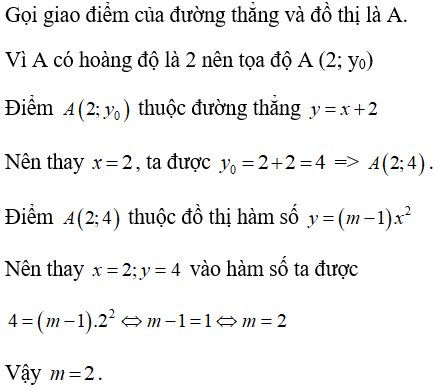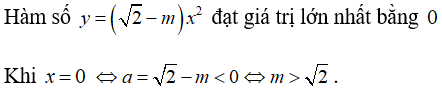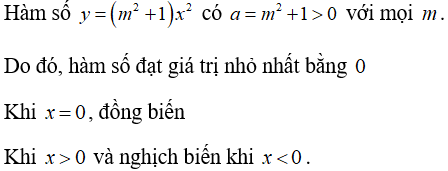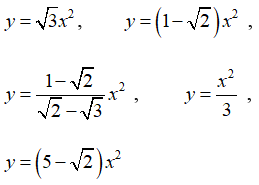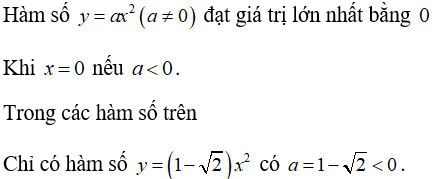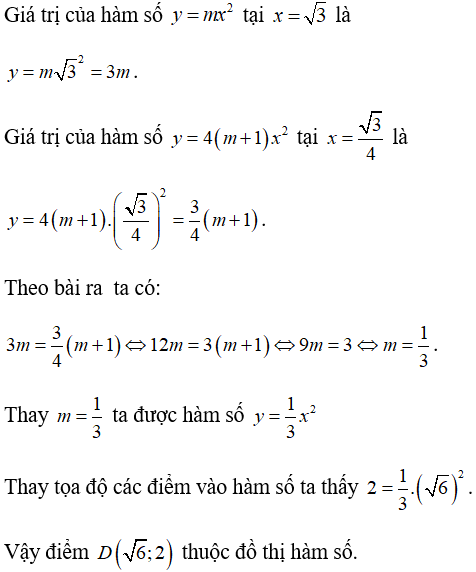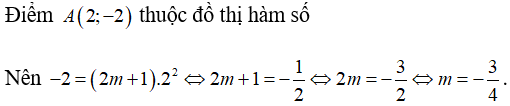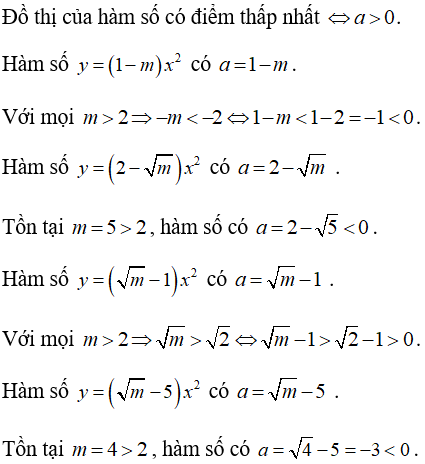Các bài toán về tham số của hàm số y = ax^2 cực hay, có đáp án | Toán lớp 9

Các bài toán về tham số của hàm số y = ax^2 cực hay, có đáp án

Với Các bài toán về tham số của hàm số y = ax^2 cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tham số của hàm số y = ax^2 từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Cho hàm số y = ax²(a ≠ 0).

Tính chất của hàm số và đồ thị.

- Nếu a > 0:

+ Hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.

+ Hàm số đạt GTNN bằng 0 tại x = 0.

+ Đồ thị hàm số nằm phía trên trục hoành, có điểm O là điểm thấp nhất của đồ thị.

- Nếu a < 0:

+ Hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.

+ Hàm số đạt GTLN bằng 0 tại x = 0.

+ Đồ thị hàm số nằm phía dưới trục hoành, có điểm O là điểm cao nhất của đồ thị.

Tìm tham số khi biết một điểm thuộc đồ thị

Bước 1: Tìm tọa độ (x; y) của một điểm thuộc đồ thị hàm số (nếu cần).

Bước 2: Thay các giá trị x; y vào hàm số, giải phương trình để tìm tham số.

Bước 3: Kết luận.

B. Các ví dụ điển hình

Ví dụ 1:Cho hàm số y = mx²(với m là tham số, m ≠ 0). Giá trị của m để đồ thị hàm số đi qua điểm C(3; 6) là:

Lời giải

Chọn A

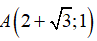
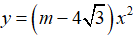
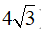
Ví dụ 2:Điểm thuộc đồ thị hàm số (với m là tham số, m ≠ ). Giá trị m là:

Lời giải

Chọn D

Ví dụ 3:Đường thẳng y = x + 2 cắt đồ thị của hàm số y = (m - 1)x² (với m là tham số, m ≠ 1) tại điểm có hoành độ bằng 2. Giá trị của tham số m là:

Lời giải

Chọn C

C. Bài tập vận dụng

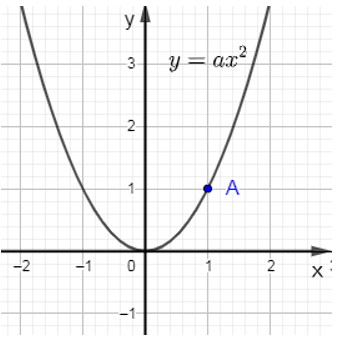
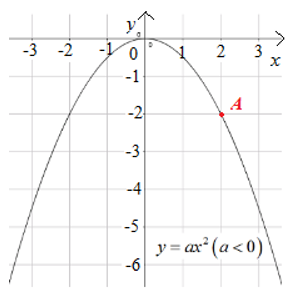
Bài 1: Cho hàm số y = ax² (a ≠ 0) có đồ thị như hình vẽ sau đây:

Giá trị của a là:

Lời giải:

Đáp án A

Bài 2: Parabol (P): y = ax² (a ≠ 0) đi qua điểm (2; 4) và tiếp xúc với đồ thị (d) của hàm số y = 2(m - 1)x + 1 - m. Tọa độ tiếp điểm là:

Lời giải:

Đáp án B

Bài 3: Giá trị của m để hàm số 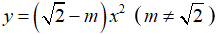đạt giá trị lớn nhất bằng 0 khi x = 0 là:

Lời giải:

Đáp án A

Bài 4: Cho hàm số y = (m² + 1)x² với m là tham số. Chọn khẳng định đúng.

Lời giải:

Đáp án B

Bài 5: Cho các hàm số sau:

Lời giải:

Đáp án D

Bài 6: Biết rằng giá trị của hàm số y = mx² tại x = √3 bằng giá trị của hàm số y = 4(m + 1)x² tại 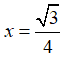(với m ≠ 0 và m ≠ -1). Điểm nào sau đây thuộc đồ thị hàm số y = mx²?

Lời giải:

Đáp án A

Bài 7: Hàm số 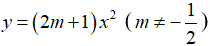có đồ thị như hình vẽ dưới đây:

Lời giải:

Đáp án B

Bài 8: Đồ thị của hàm số nào sau đây có điểm thấp nhất với mọi m > 2?

Lời giải:

Đáp án C

Bài 9: Hàm số nào sau đây có đồ thị nằm phía dưới trục hoành với mọi m?

Lời giải:

Đáp án B

Bài 10: Một bể nước hình hộp chữ nhật có đáy là hình vuông cạnh x (mét) và chiều cao của bể là m (mét, m > 0). Gọi V (m³) là thể tích của bể. Giả sử chiều cao của bể không đổi, hãy nhận xét khi cạnh x tăng lên gấp ba thì thể tích tương ứng của bể đó tăng lên bao nhiêu lần?

Lời giải:

Đáp án D