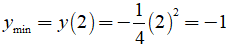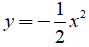Các dạng bài tập Toán 9 Chương 4 phần Đại số cực hay có đáp án | Toán lớp 9
Các dạng bài tập Toán 9 Chương 4 phần Đại số cực hay có đáp án
Với Các dạng bài tập Toán 9 Chương 4 phần Đại số cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 4 phần Đại số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Lý thuyết & Trắc nghiệm theo bài học
- Lý thuyết Bài 1: Hàm số y = ax2 (a ≠ 0) (hay, chi tiết)
- Trắc nghiệm Bài 1: Hàm số y = ax2 (a ≠ 0)
- Lý thuyết Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0) (hay, chi tiết)
- Trắc nghiệm Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
- Lý thuyết Bài 3: Phương trình bậc hai một ẩn (hay, chi tiết)
- Trắc nghiệm Bài 3: Phương trình bậc hai một ẩn
- Lý thuyết Bài 4: Công thức nghiệm của phương trình bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 4: Công thức nghiệm của phương trình bậc hai
- Lý thuyết Bài 5: Công thức nghiệm thu gọn (hay, chi tiết)
- Trắc nghiệm Bài 5: Công thức nghiệm thu gọn
- Lý thuyết Bài 6: Hệ thức Vi-ét và ứng dụng (hay, chi tiết)
- Trắc nghiệm Bài 6: Hệ thức Vi-ét và ứng dụng
- Lý thuyết Bài 7: Phương trình quy về phương trình bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 7: Phương trình quy về phương trình bậc hai
- Lý thuyết Bài 8: Giải bài toán bằng cách lập phương trình (hay, chi tiết)
- Trắc nghiệm Bài 8: Giải bài toán bằng cách lập phương trình
- Tổng hợp lý thuyết Chương 4 Đại Số 9 (hay, chi tiết)
- Tổng hợp Trắc nghiệm Chương 4 Đại Số 9
Các dạng bài tập
- Tính giá trị của hàm số tại một điểm cho trước
- Xét tính đồng biến, nghịch biến của hàm số
- Các bài toán về tham số của hàm số y = ax2
- Cách giải các bài toán về đường thẳng y = ax + b
- Cách tìm tọa độ giao điểm của parabol và đường thẳng
- Cách biện luận số giao điểm của đường thẳng và parabol
- Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm
- Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về vị trí giao điểm
- Cách giải phương trình bậc hai một ẩn
- Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn
- Cách giải phương trình bậc hai chứa tham số
- Cách giải và biện luận phương trình bậc hai theo tham số m
- Cách xét dấu các nghiệm của phương trình bậc hai
- Tìm m để phương trình có nghiệm thỏa mãn điều kiện cho trước
- Các dạng bài tập về phương trình bậc hai một ẩn
- Cách giải phương trình trùng phương
- Cách giải phương trình chứa ẩn ở mẫu
- Cách giải phương trình tích
- Các dạng bài tập Phương trình quy về phương trình bậc hai
- Cách giải bài toán về cấu tạo số bằng cách lập phương trình
- Cách giải bài toán năng suất bằng cách lập phương trình
- Cách giải bài toán chuyển động bằng cách lập phương trình
- Cách giải bài toán về diện tích hình học bằng cách lập phương trình
- Cách giải bài toán liên quan đến Vật Lí, Hóa Học, … bằng cách lập phương trình
- Các giải bài toán bằng cách lập phương trình
- Tính giá trị của hàm số bậc hai tại 1 điểm hay, chi tiết
- Cách xác định hệ số a của hàm số y = ax2 hay, chi tiết
- Cách tìm giao điểm của parabol P và đường thẳng hay, chi tiết
- Cách xác định các hệ số a, b, c của phương trình bậc hai một ẩn
- Phương pháp giải phương trình bậc hai một ẩn hay, chi tiết
- Cách giải các dạng toán giải phương trình bậc hai một ẩn cực hay
- Cách giải và biện luận phương trình bậc hai một ẩn cực hay
- Cách giải hệ phương trình 2 ẩn bậc hai cực hay, chi tiết
- Cách tìm m để hai phương trình có nghiệm chung cực hay
- Cách giải phương trình bậc nhất hai ẩn cực hay, chi tiết
- Không giải phương trình, tính tổng và tích các nghiệm của phương trình bậc hai
- Cách giải phương trình bằng cách nhẩm nghiệm cực hay
- Cách tìm hai số khi biết tổng và tích của chúng cực hay
- Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai
- Cách lập phương trình bậc hai khi biết hai nghiệm của phương trình đó
- Tìm m để phương trình bậc hai có hai nghiệm cùng dấu, trái dấu
- Cách tìm m để phương trình bậc hai có nghiệm thỏa mãn điều kiện
- Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào tham số | Tìm hệ thức liên hệ giữa x1 x2 độc lập với m
- Cách giải hệ phương trình đối xứng hai ẩn cực hay
- Phương pháp giải phương trình trùng phương cực hay
- Phương pháp giải phương trình chứa ẩn ở mẫu hay, chi tiết
- Phương pháp giải phương trình đưa về dạng tích cực hay
- Cách giải phương trình bằng phương pháp đặt ẩn phụ cực hay
- Cách giải phương trình bậc ba có một nghiệm cho trước
- Cách giải và biện luận phương trình chứa ẩn ở mẫu cực hay
- Tìm m để phương trình trùng phương vô nghiệm, có 1, 2, 3, 4 nghiệm
- Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)(x + b)(x + c)(x + d) = 0)
- Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c)
- Cách giải phương trình bậc bốn dạng ax4 + bx3 + cx2 ± kbx + k2a = 0
- Cách giải phương trình chứa căn thức lớp 9 cực hay
- Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết
- Giải bài toán bằng cách lập phương trình – Dạng toán về quan hệ giua các số, tìm số tự nhiên
- Giải bài toán bằng cách lập phương trình – Dạng toán chuyển động
- Giải bài toán bằng cách lập phương trình – Dạng toán công việc
- Giải bài toán bằng cách lập phương trình – Dạng hình học
Hàm số y = ax^2 (a ≠ 0)
1. Tập xác định
Hàm số y = ax2 (a ≠ 0) xác định với mọi giá trị của x ∈ R.
2. Tính chất
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
3. Nhận xét
+ Nếu a > 0 thì y > 0 với mọi x ≠ 0; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số y = 0.
+ Nếu a < 0 thì y < với mọi x ≠ 0; y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
4. Ví dụ cụ thể
Câu 1: Cho hai hàm số y = 2x2 và y = -2x2. Với từng giá trị của x dưới đây hãy tính giá trị của y tương ứng và nhận xét ?
Hướng dẫn:
| x | 0 | 1 | 3 | 4 |
| y = 2x2 | 0 | 2 | 18 | 32 |
| y = -2x2 | 0 | -2 | -18 | -32 |
Nhận xét:
+ Với a = 2 > 0 và giá trị x > 0 tăng dần thì giá trị tương ứng của y cũng tăng dần
⇒ Hàm số y = 2x2 đồng biến với x > 0.
+ Với a = -2 < 0 và giá trị x > 0 tăng dần thì giá trị tương ứng của y giảm dần.
⇒ Hàm số y = -2x2 nghịch biến với x > 0.
Câu 2: Một vật rơi ở độ cao so với mặt đất là 100m. Quãng đường chuyển động là s (mét) của vật rơi phụ thuộc vào thời gian là t (giây) bởi công thức: s = 4t2. Hỏi sau bao lâu vật này tiếp đất ?
Hướng dẫn:
Thời gian để vật chạm đất là:
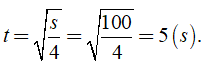
Vậy sau 5 (s) thì vật chạm đất.
B. Bài tập tự luận
Câu 1: Tìm bán kính của đường tròn khi diện tích hình tròn bằng 16π2 (cm)
Lời giải:
Câu 2: Một vật rơi tự do từ độ cao so với mặt đất là 400m. Quãng đường chuyển động của vật rơi phụ thuộc vào thời gian bởi công thức s = 4t2 ( quãng đường s(m) , thời gian là t(s) ) . Hỏi sau bao lâu, vật này chạm đất?
Lời giải:
Đồ thị hàm số y = ax^2 (a ≠ 0)
1. Đồ thị hàm số y = ax2 (a ≠ 0)
Đồ thị của hàm số y = ax2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất cảu đồ thị.
2. Cách vẽ đồ thị hàm số y = ax2 (a ≠ 0)
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số y =ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
3. Ví dụ cụ thể
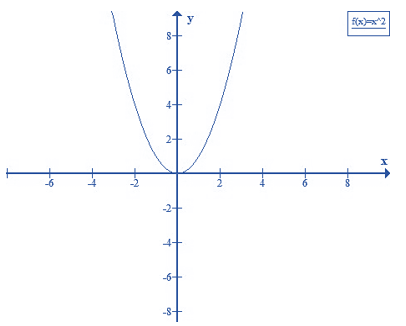
Câu 1: Vẽ đồ thị hàm số y = x2.
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = x2 | 0 | 1 | 1 | 4 | 4 |
Trên mặt phẳng tọa độ, lấy các điểm O(0;0): A(1; 1); B (-1; 1); C(2; 4) và D( -2;4) rồi lần lượt nối chúng để được đường cong như hình dưới đây.
Đồ thị của hàm số y = x2:
Câu 2: Vẽ đồ thị hàm số y = -(1/2)x2
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = -(1/2)x2 | 0 | -1/2 | -1/2 | -2 | -2 |
Đồ thị
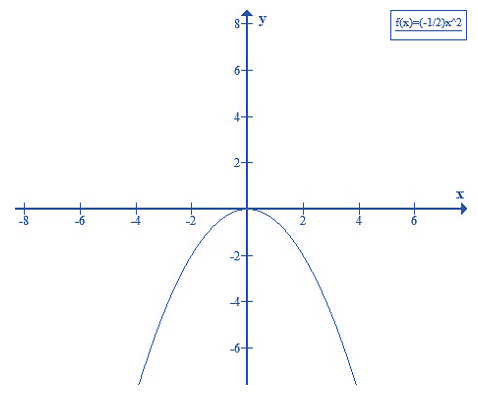
Trên mặt phẳng tọa độ lấy các điểm
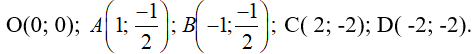
Nối các điểm đó ta được đường cong như hình vẽ dưới đây là đồ thị hàm số
B. Bài tập tự luận
Câu 1: Cho hàm số y = ax2 . Tìm giá trị nhỏ nhất của y khi x đi từ -2017 đến 2018
Lời giải:
Ta thấy rằng hệ số a của đồ thị này dương, nên đồ thị có giá trị nhỏ nhất là y = 0 tại x = 0
Nhận thấy rằng trong khoảng -2017 đến 2018 đi qua hoành độ x = 0
Do đó giá trị nhỏ nhất của hàm số y = ax2 là y(0) = 0
Vậy giá trị nhỏ nhất của y bằng 0 tại x = 0
Câu 2: Cho hàm số 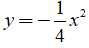
Lời giải:
Hệ số a của đồ thị này là số âm nên đồ thị này có giá trị lớn nhất là
* Khi x đi từ -1 đến 0 thì hàm số đồng biến nên trên đoạn [-1; 0] , hàm số đạt giá trị nhỏ nhất tại x = -1 và 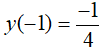
* Khi x đi từ 0 đến 2 thì hàm số nghịch biến nên hàm số đạt giá trị nhỏ nhất tại x = 2 trên đoạn
[ 0; 2] và y(2) = -1
* Suy ra, hàm số đạt giá trị nhỏ nhất tại x = 2 và