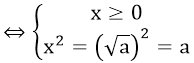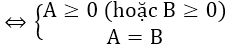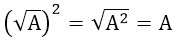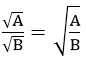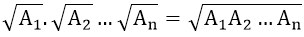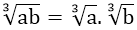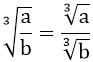Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba đầy đủ nhất | Toán lớp 9

Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba đầy đủ nhất

Tài liệu Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba đầy đủ nhất Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Chương 1: Căn bậc hai, Căn bậc ba từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

Chủ đề 1: Căn bậc hai. Căn thức bậc hai

1. Căn bậc hai số học

    - Căn bậc hai số học của số thực a không âm là số không âm x mà x² = a

    - Với a ≥ 0

x = √a

Phép toán tìm căn bậc hai số học của một số gọi là phép khai phương

Với hai số a, b không âm, thì ta có: a < b ⇔ √a < √b

2. Căn thức bậc hai

    - Cho A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.

    - √A xác định (hay có nghĩa) khi A ≥ 0

    - Hằng đẳng thức √(A²) = |A|

3. Chú ý

      +) Với a ≥ 0 thì:

√x = a ⇒ x = a²

x² = a ⇒ x = ± √a

      +) √A = √B

      +) √A + √B = 0 ⇔ A = B = 0

Chủ đề 2: Liên hệ phép nhân, phép chia với phép khai chương

1.

Với A ≥ 0, B ≥ 0 thì √(A.B) = √A . √B và ngược lại √A . √B = √(A.B)

Đặc biệt, khi A ≥ 0, ta có:

2.

Với A ≥ 0, B > 0 thì: 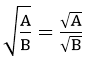và ngược lại

3. Bổ sung

      +) Với A₁, A₂, ..., A_n ≥ 0 thì

      +) Với a ≥ 0; b ≥ 0 thì 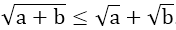. Dấu bằng xảy ra khi a = 0 hoặc b = 0

      +) Với a ≥ b ≥ 0 thì 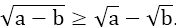. Dấu bằng xảy ra khi a = 0 hoặc b = 0

4. Các bất đẳng thức thường dùng

      +) Với a ≥ b ≥ 0 thì a + b ≥ 2√(ab)

      +) với a > 0; b > 0

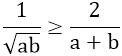
Chủ đề 3: Biến đổi đơn giản biểu thức chứa căn bậc hai

1. Đưa thừa số ra ngoài dấu căn

với B ≥ 0

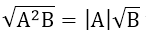
2. Đưa thừa số vào trong dấu căn

với A ≥ 0; B ≥ 0

với A < 0; B ≥ 0

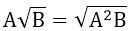
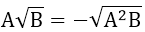
3. Khử mẫu ở biểu thức chứa căn

với AB ≥ 0; B ≠ 0

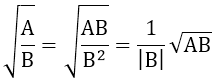
4. Trục căn thức ở mẫu

(A > 0)

(A ≥ 0 ; B ≥ 0; A ≠ B)

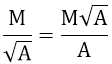
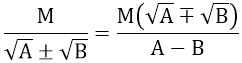
5. Rút gọn biểu thức có chứa căn bậc hai

Bước 1: Dùng các phép biến đổi đơn giản để đưa các căn thức bậc hai phức tạp thành căn thức bậc hai đơn giản.

Bước 2: Thực hiện các phép tính theo thứ tự đã biết.

Chủ đề 4: Căn bậc ba

1. Định nghĩa: Căn bậc ba của một số a, kí hiệu là ³√a là số x sao cho x³ = a.

      +) Cho a ∈ R; ³√a = x ⇔ x³ = (³√a)³ = a

      +) Mỗi số thực a đều có duy nhất một căn bậc ba

      +) Nếu a > 0 thì ³√a > 0

      +) Nếu a = 0 thì ³√a = 0

      +) Nếu a < 0 thì ³√a < 0

2. Tính chất

      +) a < b ⇔ ³√a < ³√b

      +)

      +)

3. Các phép biến đổi căn bậc ba

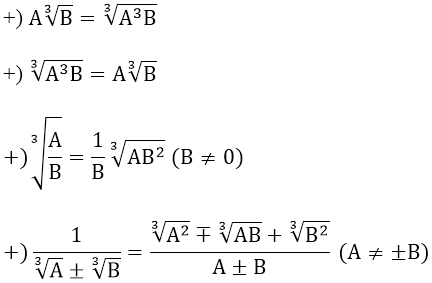
Chủ đề nâng cao 1: Dùng biểu thức liên hợp để giải toán

    - Hai biểu thức √a + √b và √a - √b gọi là hai biểu thức liên hợp.

    - Hai biểu thức 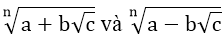trong đó a, b, c là các biểu thức, gọi là hai biểu thức liên hợp bậc n.

Khi gặp các bài tập tính toán, rút gọn,... có dạng tổng hay hiệu của hai biểu thức liên hợp thì có thể dùng phép lũy thừa để khử bớt dấu căn.