Tổng hợp lý thuyết Chương 2 Đại Số 9 hay, chi tiết | Toán lớp 9

Tổng hợp lý thuyết Chương 2 Đại Số 9 hay, chi tiết

Tài liệu Tổng hợp lý thuyết Chương 2 Đại Số 9 hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Chương 2 Đại Số từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

I. CHỦ ĐỀ 1: KHÁI NIỆM HÀM SỐ

1. Khái niệm hàm số

• Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, x được gọi là biến số.

• Hàm số có thể cho bằng bảng hoặc công thức.

• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì hàm số y được gọi là hàm hằng.

2. Đồ thị hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ Oxy.

3. Hàm số đồng biến, nghịch biến.

Cho hàm số y = f(x) xác định trên tập số thực R Với x₁, x₂ ∈ R ta có:

• Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số đồng biến.

• Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số nghịch biến.

II. CHỦ ĐỀ 2: HÀM BẬC NHẤT. ĐỒ THỊ HÀM SỐ y = ax + b (a ≠ 0)

1. Định nghĩa

• Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0

• Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax , biểu thị tương quan tỉ lệ thuận giữa y và x.

2. Tính chất.

Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R và có tính chất:

a) Đồng biến trên R, khi a > 0.

b) Nghịch biến trên R, khi a < 0.

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0) .

• Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0 ; nằm ở góc phần tư thứ II và thứ IV khi a < 0 .

• Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

• Cắt trục tung tại điểm có tung độ bằng b.

• Song song với đường thẳng y = ax nếu b ≠ 0 , và trùng với đường thẳng y = ax nếu b = 0

4. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0) .

• Bước 1: Cho x = 0 thì y = b , ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì x = -b/a ta được điểm Q(-b/a; 0) thuộc trục hoành

• Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0) .

5. Kiến thức mở rộng

Trong mặt phẳng toạ độ, cho hai điểm A(x₁; y₂) ; B(x₂; y₂) ta có:

•

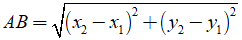
• M(x; y) là trung điểm của AB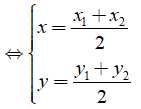

• A đối xứng với B qua trục hoành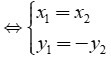

• A đối xứng với B qua trục tung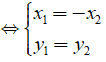

• A đối xứng với B qua gốc O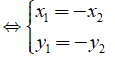

• A đối xứng với B qua đường thẳng y = x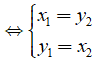

• A đối xứng với B qua đường thẳng y = -x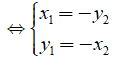

III. CHỦ ĐỀ 3. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG y = ax + b (a ≠ 0)

1. Đường thẳng song song, đường thẳng cắt nhau.

Cho hai đường thẳng (d₁ ): y = ax + b (a ≠ 0); (d₂): y = a'x + b' (a' ≠ 0)

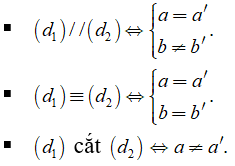
• Khi a ≠ 0 và b = b’ thì hai đường thẳng có cùng tung độ gốc, do đó chúng cắt nhau tại 1 điểm trên trục tung có tung độ là b.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

* Cho đường thẳng y = ax + b (a ≠ 0) thì a được gọi là hệ số góc của đường thẳng.

* Tính chất

• Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn.Hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90°.

• Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180°.

3. Kiến thức bổ sung

Cho hai đường thẳng (d₁): y = ax + b (a ≠ 0); (d₂): y = a'x + b' (a' ≠ 0) .

• (d₁) ⊥ (d₂) ⇔ a.a' = -1

• Nếu (d₁) cắt (d₂) thì hoành độ giao điểm là nghiệm của phương trình ax + b = a'x + b'

B. Bài tập tự luận

Câu 1: Cho hai đường thẳng (d₁): y = x - 2 và (d₂): y = 2 - x

a) Vẽ hai đường thẳng trên cùng trục

b) Tìm tọa độ giao điểm của (d₁), (d₂)

c) Vẽ đồ thị hàm số y = |x - 2|

d) Biện luận số nghiệm của phương trình m = |x - 2|

Lời giải:

a) Vẽ (d₁):

+ Cho x = 0 ⇒ y = -2

+ Cho y = 0 thì x = 2.

Đồ thị hàm số y = x - 2 là đường thẳng đi qua 2 điểm (0; -2) và (2; 0)

*Vẽ (d₂): y = 2 - x

Cho x = 0 thì y = 2

Cho y = 0 thì x = 2

Đồ thị hàm số y = 2 – x là đường thẳng đi qua 2 điểm (0; 2) và (2; 0).

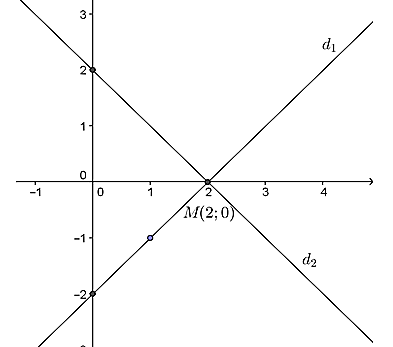
b) Hoành độ giao điểm của 2 đường thẳng đã cho là nghiệm phương trình :

x - 2 = 2 - x ⇔ 2x = 4 ⇔ x = 2

Với x = 2 ⇒ y = 2 - 2 = 0

Vậy tọa độ giao điểm là M(2; 0)

c) Ta có:

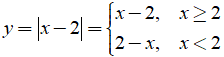
Nhận xét: y = x - 2 nếu x ≥ 2 là nửa đường thẳng nằm trên nửa mặt phẳng bờ là đường thẳng x = 2

Kết luận: Đồ thị y = |x - 2| như hình vẽ

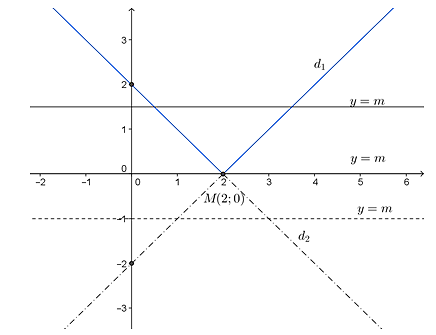
d) Xét hai đồ thị: y = m, y = |x - 2|

Số nghiệm của phương trình m = |x - 2| là số giao điểm của đồ thị y = m và y = |x - 2|

+ Với m < 0 đường thẳng y = m không cắt đồ thị hàm số y = |x - 2| . Như vậy phương trình đã cho vô nghiệm.

+ Với m = 0 đường thẳng y = m cắt đồ thị hàm số y = |x - 2| tại một điểm duy nhất. Như vậy phương trình đã cho có 1 nghiệm duy nhất.

+ Với m > 0 đường thẳng y = m cắt đồ thị hàm số y = |x - 2| tại hai điểm phân biệt. Như vậy phương trình đã cho có hai nghiệm phân biệt.

Câu 2: Xác định các hệ số a và b để đường thẳng y = ax + b cắt trục tung tại điểm có tung độ bằng -2 và song song với đường thẳng OA, trong đó O là gốc tọa độ và điểm A(2; 1)

Lời giải:

Đường thẳng OA đi qua O nên có dạng: y = ax (a ≠ 0) .

Điểm A nằm trên đường thẳng OA nên: 1 = a.2 ⇒ a = 1/2

Vậy phương trình đường thẳng OA là y = 1/2

Vì đường thẳng y = ax + b song song với đường thẳng OA nên a = 1/2

Mặt khác đường thẳng đó đi qua điểm có tọa độ là (0; -2)

Khi đó ta có: -2 = 0.1/2 + b ⇒ b = -2

Vậy giá trị cần tìm là a = 1/2; b = -2

Câu 3: Lập phương trình đường thẳng đi qua M(-1; -2) và thỏa mãn:

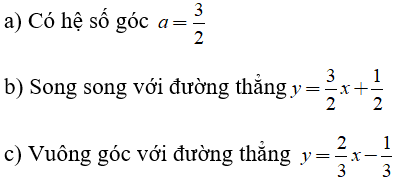
Lời giải:

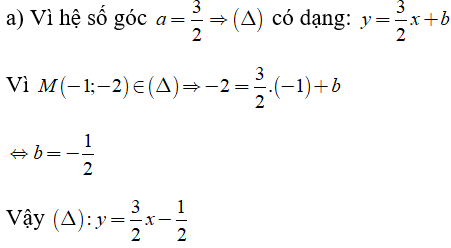
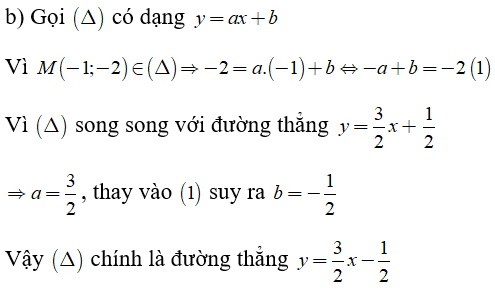
Câu 4: Cho hai hàm số y = (m + 3)x - 1 (1) và y = (1 - 2m)x + 5 (2)

Với giá trị nào của m thì đồ thị hai hàm số là hai đường thẳng

a) Song song

b) Cắt nhau

c) Trùng nhau

Lời giải:

Xét (1) ta có: a = m + 3, b = -1

Xét (2) ta có: a' = 1 - 2m, b' = 5

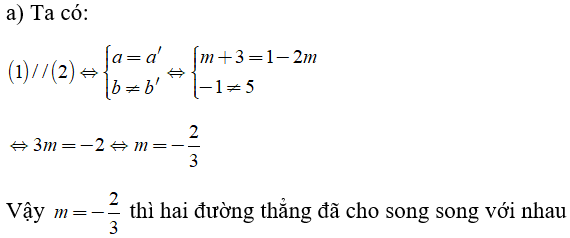
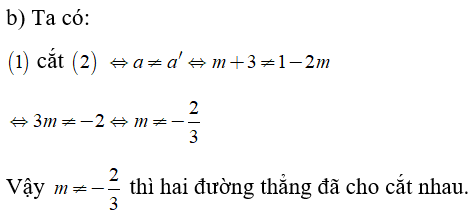
Câu 5: Cho hàm số y = (m - 1)x + m (d)

a) Tìm điểm M cố định mà đồ thị đi qua với mọi m

b) Viết đường thẳng đi qua điểm M và gốc tọa độ

c) Tìm m để khoảng cách từ O đến (d) là lớn nhất.

Lời giải:

a) Gọi M(x₀; y₀) là điểm cố định mà đồ thị hàm số đi qua với mọi m

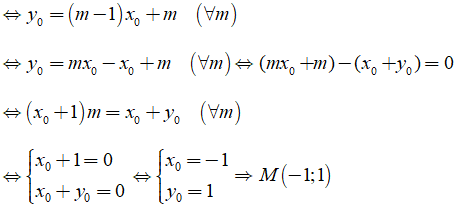
b) Vì đường thẳng OM đi qua gốc tọa độ O

Nên phương trình có dạng : y = ax (a ≠ 0)

Điểm M(-1; 1) thuộc đường thẳng OM nên

1 = a.(-1) nên a = -1

Vậy phương trình đường thẳng OM là y = -x

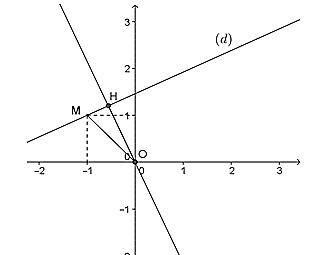
c) Gọi H là hình chiếu của O lên (d)

Ta có: OH ≤ OM (không đổi)

Vậy để OH đạt giá trị lớn nhất thì đường thẳng (d) vuông góc với đường thẳng OM

⇔ (m - 1)(-1) = -1 ⇔ m = 2

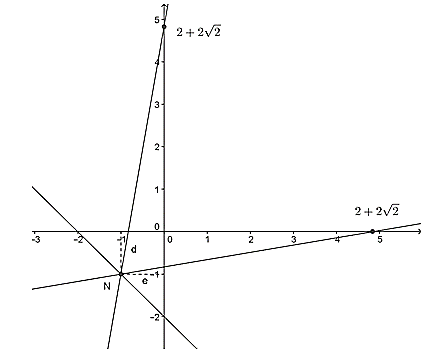
Câu 6: Cho đường thẳng y = mx + m - 1 (m là tham số) (1)

a) Chứng minh rằng đường thẳng (1) luôn đi qua một điểm cố định với mọi giá trị của m

b) Tìm giá trị của m để đường thẳng (1) tạo với các trục tọa độ một tam giác có diện tích bằng 2.

Lời giải:

a) Điều kiện để đường thẳng (1) đi qua điểm N(x₀; y₀) với mọi m là:

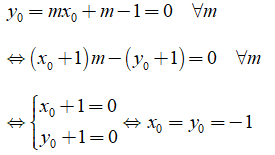
Vậy đường thẳng (1) luôn đi qua điểm cố định là N(-1; -1)

b) Gọi A là giao điểm của đường thẳng (1) với trục tung

Với x = 0 ⇒ y = m - 1 ⇒ A(0; m - 1) . Do đó: OA = |m - 1|

Gọi B là giao điểm của đường thẳng (1) với trục hoành

Với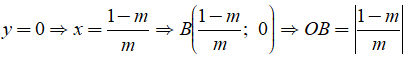

Ta có:

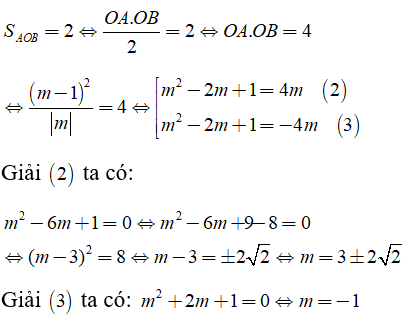
Có 3 đường thẳng đi qua điểm N tạo với các trục tọa độ một tam giác có diện tích bằng 2

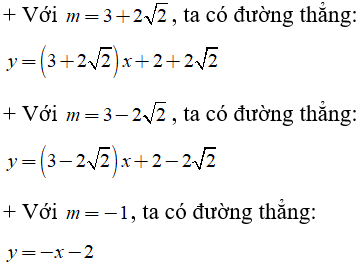
Câu 7: Tìm m để hai đường thẳng cắt nhau tại một điểm thuộc góc phần tư thứ nhất; góc phần tư thứ hai với mx + 2y = 5 (1) và 2x + y = 1 (2)

Lời giải:

Hai đường thẳng cắt nhau khi và chỉ khi

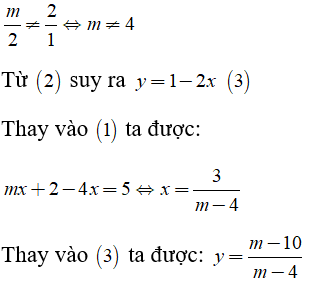
+ Hai đường thẳng cắt nhau tại một điểm thuộc góc phần tư thứ nhất khi:

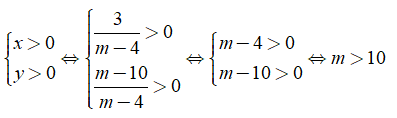
+ Hai đường thẳng cắt nhau tại một điểm thuộc góc phần tư thứ hai khi:

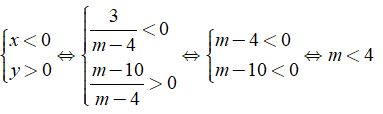
Câu 8: Vẽ đồ thị các hàm số sau:

a) y = 2|x - 2| - 3

b) y = |x - 1| + |x - 3|

Lời giải:

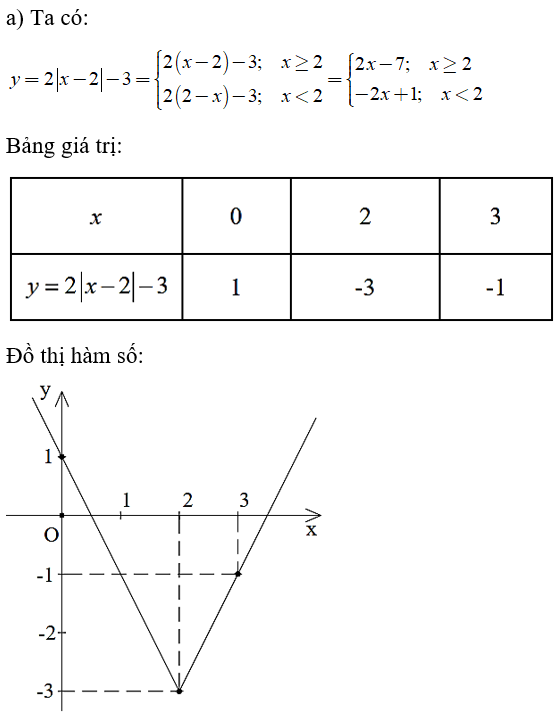
b) Ta có: y = |x - 1| + |x - 3|

Bảng xét dấu:

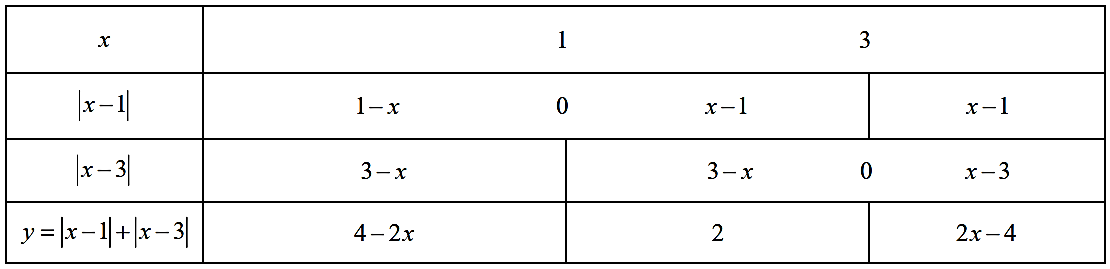
Dựa vào bảng trên ta có:

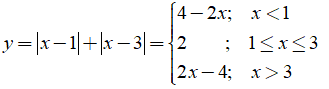
Bảng giá trị:

Đồ thị hàm số:

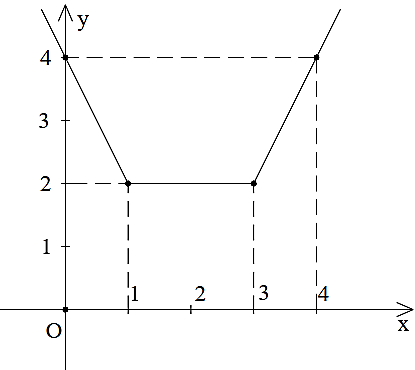
Câu 9: Tìm m để ba đường thẳng sau đồng quy:

(d₁ ):y = 2x - 3, (d₂): y = x - 1, (d₃): y = (m - 1)x + 2m

Lời giải:

Hoành độ giao điểm của (d₁); (d₂) là nghiệm của hệ phương trình:

Câu 10: Cho điểm B(4; 1). Đường thẳng (d) đi qua B cắt Ox, Oy theo thứ tự tại I(a; 0), J(0; b) với a, b > 0

a) Viết phương trình đường thẳng d để diện tích Δ OIJ nhỏ nhất

b) Tìm b để (OI + OJ) nhỏ nhất

Lời giải:

a) Đường thẳng d đi qua B cắt Ox, Oy tại I (a; 0) và J(0; b) nên phương trình đường thẳng d:

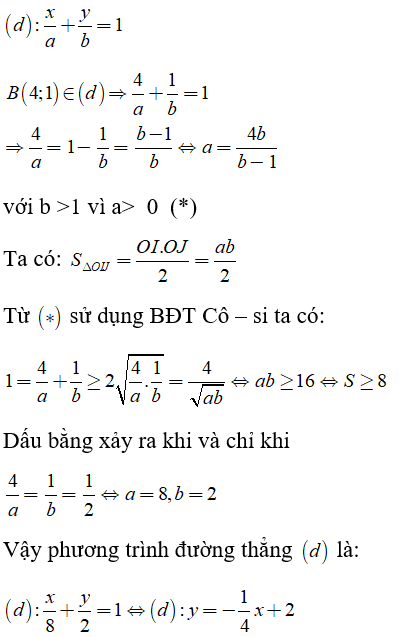
b) Ta có: