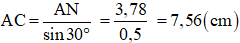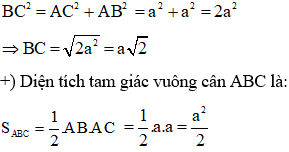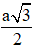Cách tính cạnh và tính góc trong tam giác vuông cực hay | Toán lớp 9

Cách tính cạnh và tính góc trong tam giác vuông cực hay

Với Cách tính cạnh và tính góc trong tam giác vuông cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính cạnh và tính góc trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

Nhắc lại kiến thức

Trong một tam giác vuông, nếu cho trước hai cạnh hoặc một cạnh và một góc nhọn thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của nó.

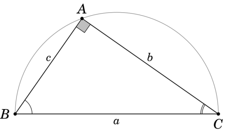
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c.

1. Định lý: Trong một tam giác vuông, mỗi cạnh góc vuông bằng

- Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

- Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.

2. Như vậy, trong tam giác ABC vuông tại A, ta có hệ thức

• b = a.sinB = a.cosC = c.tanB = c.cotC

• c = a.sinC = a.cosB = b.tanC = b.cotB

A. Phương pháp giải

• Kẻ thêm đường cao xuống cạnh kề của góc đã biết.

• Chuyển bài toán về giải tam giác vuông biết một cạnh và một góc.

B. Ví dụ minh họa

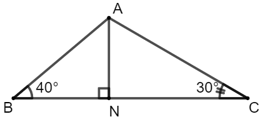
Ví dụ 1: Cho tam giác ABC, trong đó BC = 11cm, 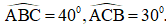. Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC. Hãy tính

a) Độ dài đoạn thẳng AN.

b) Độ dài cạnh AC.

Hướng dẫn giải:

a) Xét tam giác vuông ANB có: AN = BN.tan40^o

Xét tam giác vuông ANC có: AN = CN.tan30^o

⇒ AN = BN.tan40^o = CN.tan30^o

Mà BN = BC – CN = 11 – CN

⇒ (11 - CN). tan40^o = CN.tan30^o

⇔ (11 - CN).0,84 = CN.0,58

⇔ 9,24 - 0,84.CN = 0,58CN

⇔ 1,42.CN = 9,24

⇔ CN ≈ 6,51 (cm)

⇒ AN = CN.tan30^o ≈ 6,51.0,58 ≈ 3,78 (cm)

b) Xét tam giác vuông ANC có:

Ví dụ 2: Tính cạnh huyền và diện tích của một tam giác vuông cân nếu a là cạnh góc vuông.

Hướng dẫn giải:

+) Xét tam giác ABC vuông cân tại A có AB = AC = a.

Áp dụng định lý Py – ta – go ta có:

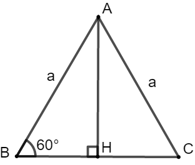
Ví dụ 3: Tính chiều cao và diện tích của một tam giác đều cạnh a.

Hướng dẫn giải:

Xét tam giác ABC đều có cạnh AB = AC = BC = a và có đường cao AH.

Do ΔABC là tam giác đều nên đường cao AH đồng thời cũng là đường trung tuyến tại đỉnh A

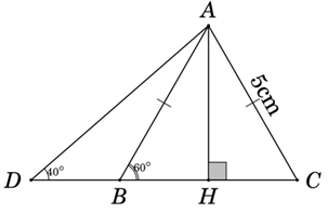
Ví dụ 4: Cho tam giác đều ABC cạnh 5cm và góc 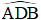= 40^o Hãy tính

a) Độ dài đoạn AD.

b) Độ dài đoạn DB.

Hướng dẫn giải:

a) Xét tam giác ABC đều cạnh AB = AC = BC = 5cm

Suy ra độ dài đường cao AH của tam giác đều ABC là AH =

b) Xét tam giác ABC đều có cạnh AB = AC = BC = a và có đường cao AH.

Do ΔABC là tam giác đều nên đường cao AH đồng thời cũng là đường trung tuyến tại đỉnh A

⇒ BH = CH = 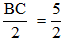= 2,5 (cm)

⇒ DB = HD - BH = 5,16 - 2,5 = 2,66 (cm)

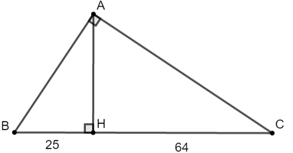
Ví dụ 5: Cho tam giác ABC vuông tại A đường cao AH. Biết HB = 25cm, HC = 64cm. Tính , .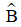

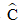
Hướng dẫn giải:

+) Xét ΔABC vuông tại A có đường cao AH nên:

AH² = BH.CH (hệ thức lượng trong tam giác vuông)

⇔ AH² = 25.64 = 1600

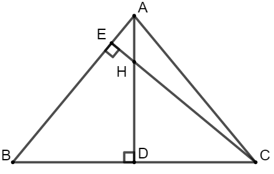
Ví dụ 6: Cho tam giác ABC có AB = AC = 50cm, BC = 60cm. Các đường cao AD và CE cắt nhau tại H.

a) Tính độ dài CE.

b) Tính độ dài CH.

Hướng dẫn giải:

a) Tam giác ABC có AB = AC = 50cm ⇒ ΔABC cân tại A có AD là đường cao nên AD đồng thời là đường trung tuyến và phân giác tại đỉnh A