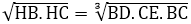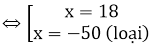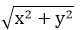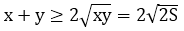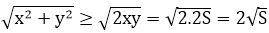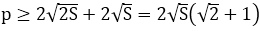Bài tập Hệ thức về cạnh và đường cao trong tam giác vuông chọn lọc, có lời giải | Toán lớp 9

Bài tập Hệ thức về cạnh và đường cao trong tam giác vuông chọn lọc, có lời giải

Với Bài tập Hệ thức về cạnh và đường cao trong tam giác vuông chọn lọc, có lời giải Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ thức về cạnh và đường cao trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

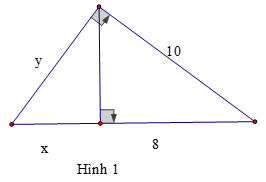
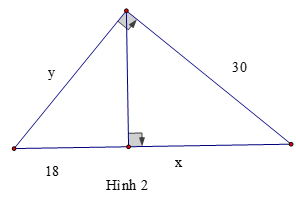
Bài 1: Tính x, y trong mỗi hình sau:

Bài 2: Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH

Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC

Bài 5: Cho tam giác ABC vuông tại A, đường cao AH

    Cho biết AC/AB = √2; HC - HB = 2cm.Tính:

    a) Tỉ số HC : HB

    b) Các cạnh của tam giác ABC

Bài 6: Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Trên HB, HC lần lượt lấy các điểm M, N sao cho góc AMC bằng góc ANB bằng 90⁰. Chứng minh rằng AM = AN

Bài 7: Cho tam giác ABC đường cao AH. Vẽ HD ⊥ AB. Tia phân giác của góc AHC cắt AC tại F. Biết AB = 6cm, AC = 8cm, BC = 10 cm. Tính:

    a) Độ dài AH

    b) Chu vi tam giác ADF

Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng

Bài 9: Cho tam giác ABC vuông tại A có diện tích S không đổi. Gọi p là chu vi của nó. Tìm giá trị nhỏ nhất của p.

Đáp án và hướng dẫn giải

Bài 1:

    a) x = 4,5 và y = 7,5

    b) Áp dụng hệ thức b² = a.b' ta được: 30² = x(x + 32)

    x² + 32x - 900 = 0 ⇔ (x - 18)(x + 50) = 0

    y² = 18(18 + 18) ⇒ y = 18√2

Bài 2:

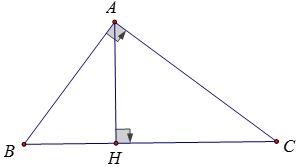
    Vẽ AH ⊥ BC

    Ta có: AB² = BH.BC ; AC² = CH.BC

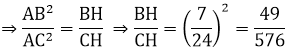
    Ta có:

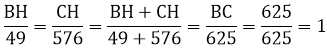
    ⇒ BH = 49.1 = 49; CH = 576.1 = 576

Bài 3:

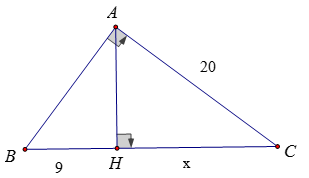
    Đặt HC = x. Áp dụng hệ thức AC² = BC.HC

    ⇒ 20² = (9 + x)x

    ⇔ x² + 9x - 400 = 0

    ⇔ (x + 25)(x - 16) = 0

    ⇔ x = -25 (loại); x = 16

    Vậy BC = 16 + 9 = 25 cm

    Ta có: AH² = HB.HC = 9.25 ⇒ AH = 15 (cm)

Bài 4:

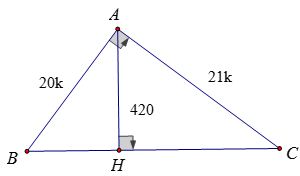
    Đặt AB = 20k ⇒ AC = 21k

    Áp dụng định lí Pytago, tính được BC = 29k

    Áp dụng hệ thức AB. AC = AH. BC

    ⇒ 20k.21k = 420.29k ⇒ k = 29

    Do đó: AB = 580; AC = 609; BC = 841

    Khi đó, chu vi của tam giác ABC là 2030

Bài 5:

    a) Ta có: AB² = BH.BC ; AC² = CH.BC

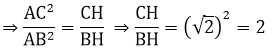
    b) Ta có: HC - HB = 2; CH/BH = 2

    ⇒ HC = 4; HB = 2; BC = 6 (cm)

    Vì AB² = BH.BC nên AB = √2.6 = 2√3 (cm)

    AC² = CH.BC nên AC = √4.6 = 2√6 (cm)

Bài 6:

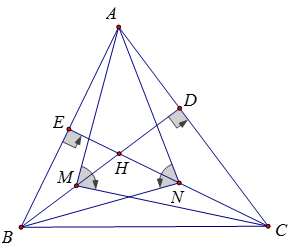
    Áp dụng hệ thức b² = a.b' vào các tam giác vuông AMC và ANB ta được:

    AM² = AC.AD ; AN² = AE.AB

    ΔABD ~ ΔACE (g.g)

    ⇒ AB/AC = AD/AE ⇒ AC.AD = AE.AB

    ⇒ AM² = AN² hay AM = AN

Bài 7:

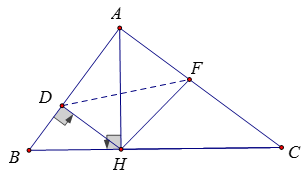
    a) Ta có: AB = 6cm; AC = 8cm; BC = 10cm

    Vì 6² + 8² = 100 = 10²

    Nên AB² + AC² = BC²

    Áp dụng định lý đảo của định lý Py - ta - go

    Suy ra tam giác ABC vuông tại A

    Ta có: AB. AC = AH. BC

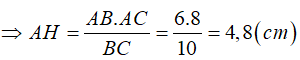
    b) Xét tam giác ABH vuông tại H, có:

    AH² = AB.AD

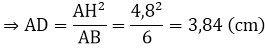
    Xét tam giác ABC vuông tại A có:

    AC² = BC.HC

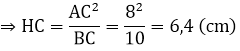
    Xét tam giác AHC có HF là đường phân giác nên

    Áp dụng định lí Pytago vào tam giác ADF vuông tại A có:

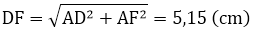
    Vậy chu vi tam giác ADF là:

    3,84 + 24/7 + 5,15 = 12,4 (cm)

Bài 8:

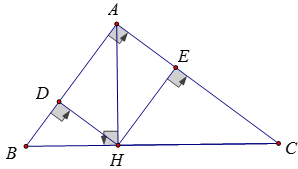
    ΔABC vuông tại A, AH là đường cao nên AH² = HB.HC

    ⇔ AH⁴ = HB².HC²

    Lại có: HB² = AB.BD; HC² = AC.CE

    ⇔ AH⁴ = AB.BD.AC.CE

    Nhưng AB. AC = AH. BC nên AH⁴ = AH.BC.BD.CE

    Do đó: AH³ = BC.BD.CE

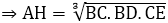
    Vì AH² = HB.HC nên

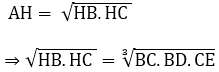
Bài 9:

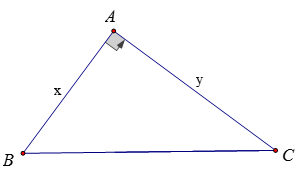
    Gọi độ dài hai cạnh góc vuông là x và y

    ⇒ độ dài cạnh huyền là

    Ta có:

    Mặt khác:

    Do đó:

    Vậy minp = 2√S (√2 + 1) khi ∆ABC vuông cân.