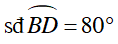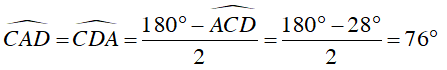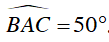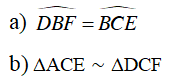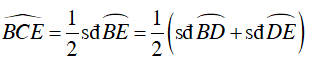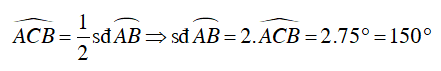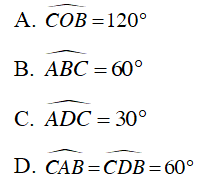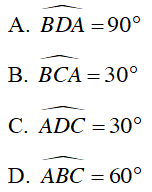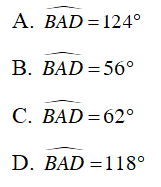Cách tính số đo góc nội tiếp cực hay, chi tiết | Toán lớp 9
Cách tính số đo góc nội tiếp cực hay, chi tiết
Với Cách tính số đo góc nội tiếp cực hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính số đo góc nội tiếp từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
A. Phương pháp giải
Ta áp dụng các kiến thức sau để tính số đo góc nội tiếp:
1. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
2. Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Ví dụ minh họa
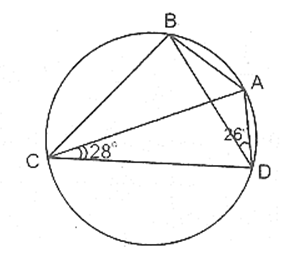
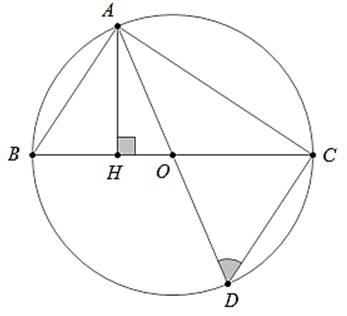
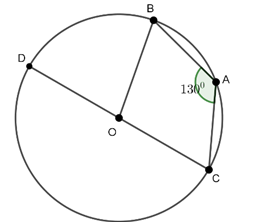
Ví dụ 1 : Cho hình vẽ có CA = CD. Hãy tính số đo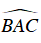 
.
Hướng dẫn giải
Xét tam giác ACD có CA = CD nên ΔACD cân tại C
⇒ 
Mà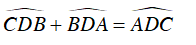 
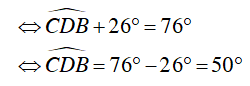
Ta lại có: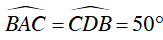 
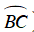
(hai góc nội tiếp cùng chắn 
).
Vậy 
Ví dụ 2 : Cho đường tròn (O; R) đường kính BC cố định. Điểm A di động trên đường tròn khác B và C. Vẽ đường kính AOD. Xác định vị trí điểm A để diện tích ΔABC đạt giá trị lớn nhất, khi đó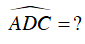 
Hướng dẫn giải
Kẻ đường cao AH của tam giác ABC
Diện tích tam giác ABC là: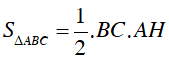 
Vì BC là đường kính nên BC cố định
Suy ra diện tích tam giác ABC đạt giá trị lớn nhất khi AH lớn nhất
Xét tam giác AHO vuông tại H, Ta có AH ≤ AO ( AO là cạnh huyền)
⇒
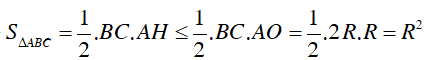
Dấu “=” xảy ra khi H ≡ O.
Khi đó A là điểm chính giữa cung BC hay AD ⊥ BC.
Xét tam giác ACD, có:
(góc nội tiếp chắn nửa đường tròn)
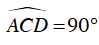
Ta có CO vừa là đường trung tuyến, vừa là đường cao
Suy ra ΔACD vuông cân tại C
⇒ 
.
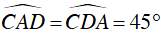
Vậy diện tích tam giác ABC lớn nhất khi A nằm chính giữa cung BC và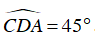 
.
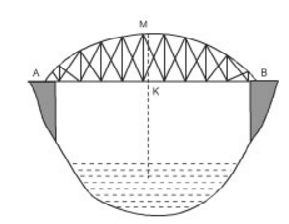
Ví dụ 3 : Một chiếc cầu được thiết kế như hình 21 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.
Hướng dẫn giải
Gọi (O; R) là đường tròn chứa cung AMB.
Kẻ đường kính MC.
K là trung điểm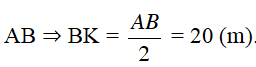 
.
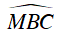
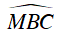
là góc nội tiếp chắn nửa đường tròn
⇒ = 90º
⇒ ΔMBC vuông tại B, có BK là đường cao
⇒ BK2 = MK.KC ( hệ thức về cạnh và đường cao trong tam giác vuông)
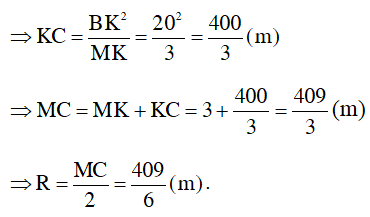
Vậy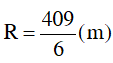 
.
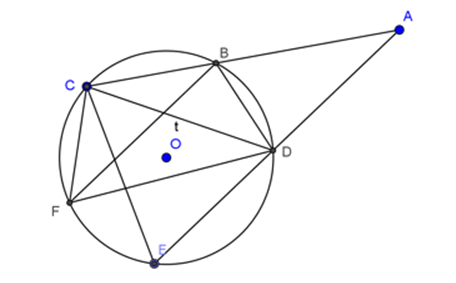
Ví dụ 4 : Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, D nằm giữa A và E). Kẻ dây BF // DE. Chứng minh rằng:
Hướng dẫn giải
a) Ta có: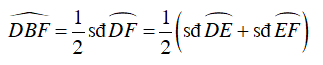 
và 
Mặt khác DE // BF
⇒ 
(hai góc so le trong)
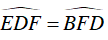
Mà 
là góc nội tiếp chắn cung 
là góc nội tiếp chắn cung 
⇒ 
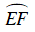
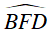
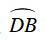
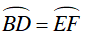
Ta lại có: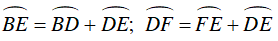 
Từ đó suy ra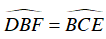 
.
b) Vì BF // DE nên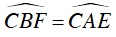 
(hai góc đồng vị)
Mà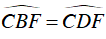 
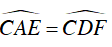
(hai góc nội tiếp cùng chắn cung CF) ⇒ 
Lại có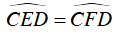 
(hai góc nội tiếp cùng chắn cung CD)
Xét ΔACE và ΔDCF, ta có:
(cmt)
(cmt)
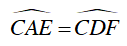
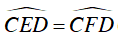
Suy ra ΔACE ∼ ΔDCF (g.g)
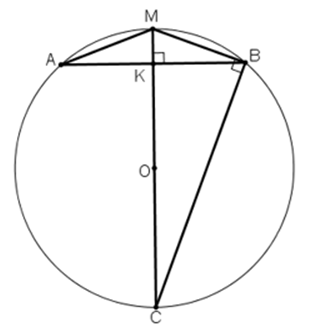
Ví dụ 5 : Cho AB và CD là hai đường kính vuông góc với nhau của đường tròn (O; R). Qua điểm M thuộc cung nhỏ AC (M ≠ A, M ≠ E) kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E, F.
a) Chứng minh: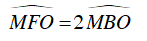 
b) Xác định vị trí điểm M trên cung nhỏ AC sao cho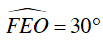 
. Khi đó tính độ dài đoạn thẳng OE, ME, EF theo R.
Hướng dẫn giải
a) Ta có: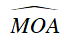 
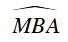
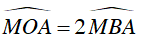
là góc ở tâm chắn cung MA
là góc nội tiếp chắn cung MA
⇒ 
Vì EF là tiếp tuyến với (O) tại M nên OM ⊥ EF
Ta có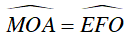 
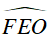
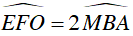
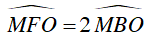
(cùng phụ với 
)
⇒ 
hay 
b)
Xét ΔAOM có: OA = OM
⇒ ΔAOM cân tại O
Ta có: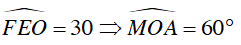 
ΔAOM đều nên AM = OA = R.
Vậy nếu M ∈ (O) và AM = R thì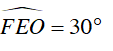 
Xét ΔOME vuông tại M, ta có:
.
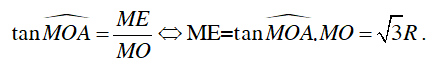
Ta có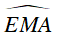 
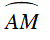
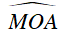
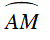
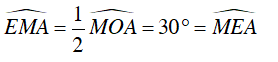
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung 
là góc ở tâm chắn cung
⇒ 
⇒ ΔMEA cân tại A
⇒ AE = AM
Mà AE = OA = OM, OE = OA+EA
⇒ OE = 2MO = 2R
Vì ΔEOF vuông tại O, ta có:
.
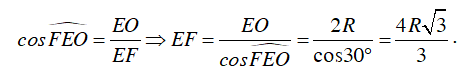
C. Bài tập trắc nghiệm
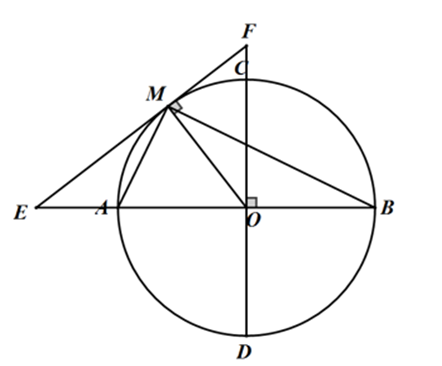
Câu 1 : Cho tam giác ABC nội tiếp đường tròn tâm (O), biết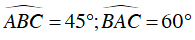 
.
Tính số đo của cung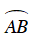 
.
A. 150o
B. 90o
C. 120o
D. 210o
Hướng dẫn giải
Đáp án A
Xét ΔABC , ta có:
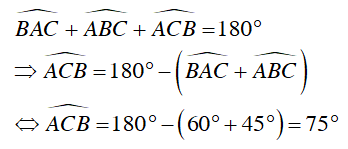
Vì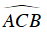 
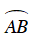
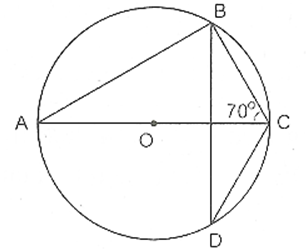
là góc nội tiếp chắn nên:
Câu 2 : Hãy tính số đo góc BDC trong hình.
A. 20o
B. 30o
C. 60o
D. 70o
Hướng dẫn giải
Đáp án A
Ta có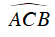 
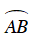
là góc nội tiếp chắn
Và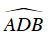 
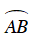
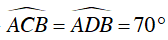
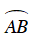
là góc nội tiếp chắn
⇒ 
(hai góc nội tiếp cùng chắn )
Ta lại có: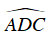 
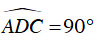
là góc nội tiếp chắn nửa đường tròn
⇒ .
Mà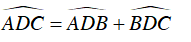 
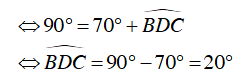
Vậy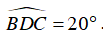 
.
Câu 3 : Cho đường tròn tâm O và 2 đường kính AB và CD. Biết rằng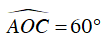 
. Tìm khẳng định sai ?
Hướng dẫn giải
Đáp án B
+ Ta có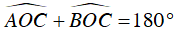 
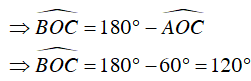
(hai góc kề bù)
Suy ra A đúng.
+ 
và 
là các góc nội tiếp chắn cung 
là góc ở tâm chắn cung
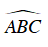
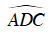
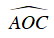
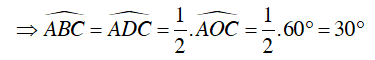
Suy ra B sai, C đúng.
+ 
và 
là các góc nội tiếp chắn cung 
là góc ở tâm chắn cung
.
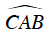
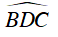
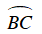
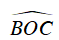
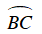
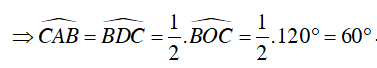
Suy ra D đúng.
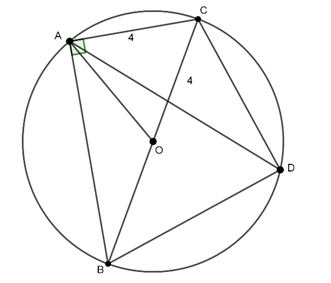
Câu 4 : Cho tam giác ABC vuông tại A nội tiếp đường tròn (O; 4) .Biết rằng AC = 4cm . Lấy D là điểm bất kì khác A, B,C trên đường tròn. Chọn khẳng định đúng.
Hướng dẫn giải
Đáp án C
Xét ΔAOC , có: OA = OC = AC = 4cm
Suy ra ΔAOC đều
. Suy ra B sai.
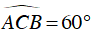
Ta có: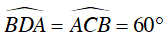 
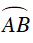
(hai góc nội tiếp cùng chắn 
). Suy ra A sai.
Xét ΔABC vuông tại A, ta có :
(hai góc nhọn phụ nhau)
. Suy ra D sai.
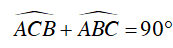
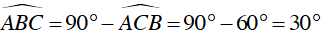
Ta lại có: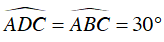 
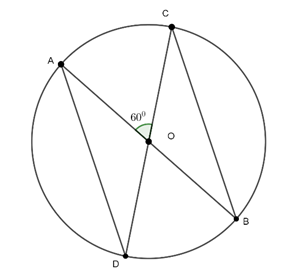
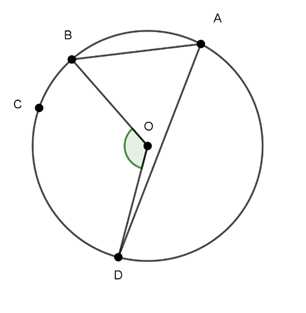
(hai góc nội tiếp cùng chắn ). Suy ra C đúng.
Câu 5 : Cho bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm O. Biết góc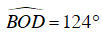 
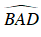
. Khi đó số đo góc 
là :
Hướng dẫn giải
Đáp án C
Ta có :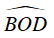 
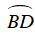
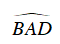
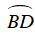
là góc ở tâm chắn 
.
là góc nội tiếp chắn .
Khi đó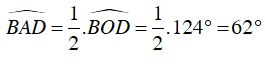 
.
Câu 6 : Cho đường tròn (O) và góc nội tiếp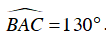 
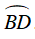
. Gọi D là giao điểm của OC và đường tròn (O). Tính số đo góc cung 
.
Hướng dẫn giải
Đáp án A
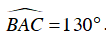
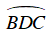
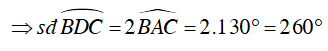
Ta có là góc nội tiếp chắn 
Khi đó số đo cung BC nhỏ là :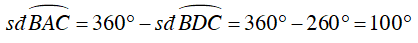 
Ta lại có :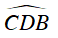 
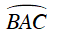
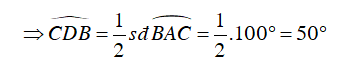
là góc nội tiếp chắn cung 
Xét ΔOBD có : OD = OB
⇒ ΔOBD cân tại O
(góc 
là góc ở tâm chắn cung BD)
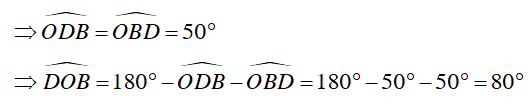
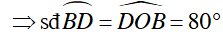
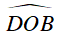
Vậy 
.
