Lý thuyết Phương trình quy về phương trình bậc hai hay, chi tiết | Toán lớp 9

Lý thuyết Phương trình quy về phương trình bậc hai hay, chi tiết

Tài liệu Lý thuyết Phương trình quy về phương trình bậc hai hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Phương trình quy về phương trình bậc hai từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Phương trình trùng phương

Phương trình trùng phương là phương trình có dạng ax⁴ + bx² + c = 0 (a ≠ 0)

Giải phương trình ax⁴ + bx² + c = 0 (a ≠ 0)

    + Đặt ẩn phụ x² = t, t ≥ 0

    + Giải phương trình ẩn phụ mới: at² + bt + c = 0

    + Với mỗi giá trị tìm được của t, lại giải phương trình x² = t.

Ví dụ: Giải phương trình x⁴ - 13x² + 36 = 0

Hướng dẫn:

Đặt x² = t, t ≥ 0 Khi đó ta được phương trình bậc hai đối với ẩn t là t² - 13t + 36 = 0 (*)

Ta có: Δ_t = (-13)² - 4.36 = 169 - 144 = 25 > 0

Khi đó phương trình (*) có hai nghiệm là:

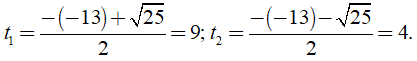
    + Với t₁ = 9 ta có x² = 9 có hai nghiệm là x₁ = 3; x₂ = -3.

    + Với t₂ = 4 ta có x² = 4 có hai nghiệm là x₁ = 2; x₂ = -2.

2. Phương trình chứa ẩn ở mẫu

Khi giải phương trình chứa ẩn ở mẫu thức, ta làm như sau:

    + Bước 1: Tìm điều kiện xác định của phương trình

    + Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức

    + Bước 3: Giải phương trình vừa nhận được

    + Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho.

Ví dụ: Giải phương trình

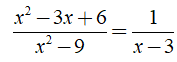
Hướng dẫn:

Điều kiện x ≠ ±3.

Khi đó ta có

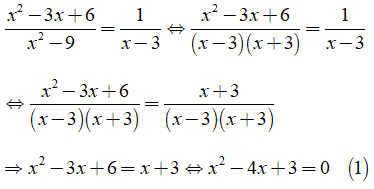
Ta có: Δ₁ = (-4)² - 4.3 = 16 - 12 = 4 > 0

Khi đó, phương trình (1) có hai nghiệm là:

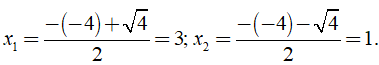
Kết hợp điều kiện, vậy phương trình có hai nghiệm là x = 1

3. Phương trình tích

Ta có: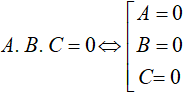

Để đưa phương trình đã cho về phương trình tích ta dùng phương pháp: đặt nhân tử chung, nhóm hạng tử, phương pháp thêm bớt hay sử dụng hằng đẳng thức đáng nhớ..

B. Bài tập tự luận

Câu 1: Giải phương trình (x² + 2x - 5)² = (x² - x + 5)²

Lời giải:

Câu 2: Giải phương trình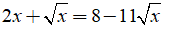

Lời giải: