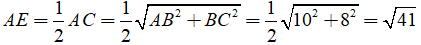Lý thuyết Sự xác định đường tròn. Tính chất đối xứng của đường tròn hay, chi tiết | Toán lớp 9

Lý thuyết Sự xác định đường tròn. Tính chất đối xứng của đường tròn hay, chi tiết

Tài liệu Lý thuyết Sự xác định đường tròn. Tính chất đối xứng của đường tròn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Sự xác định đường tròn. Tính chất đối xứng của đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định nghĩa về đường tròn

Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách điểm O một khoảng R kí hiệu là (O; R) hay (O).

Nếu A nằm trên đường tròn (O; R) thì OA = R.

Nếu A nằm trong đường tròn (O; R) thì OA < R.

Nếu A nằm ngoài đường tròn (O; R) thì OA > R.

Bổ sung kiến thức:

    + Đường tròn đi qua các điểm A₁, A₂, ..., A_n gọi là đường tròn ngoại tiếp đa giác A₁A₂...A_n

    + Đường tròn tiếp xúc với tất cả các cạnh của đa giác A₁A₂...A_n gọi là đường tròn nội tiếp đa giác đó.

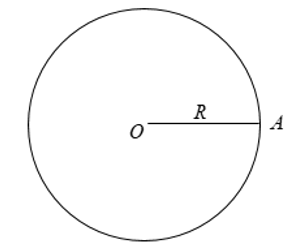
2. Cách xác định đường tròn

    + Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp tam giác vuông đó

    + Trong tam giác đều , tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.

    + Trong tam giác thường:

Tâm đường tròn ngoại tiếp là giao điểm của 3 đường trung trực của 3 cạnh tam giác đó

Tâm đường tròn nội tiếp là giao điểm 3 đường phân giác trong của tam giác đó

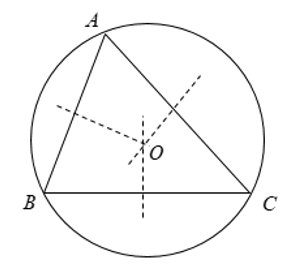
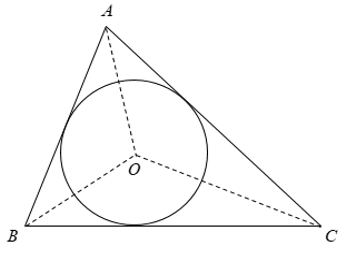
Chú ý: Không vẽ được đường tròn nào đi qua 3 điểm thẳng hàng

3. Tâm đối xứng

Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.

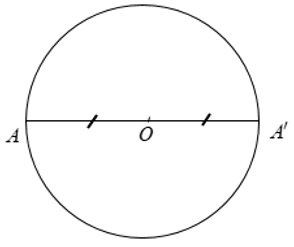
4. Trục đối xứng

Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào của đường tròn cũng là trục đối xứng của đường tròn.

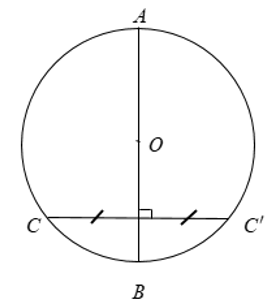
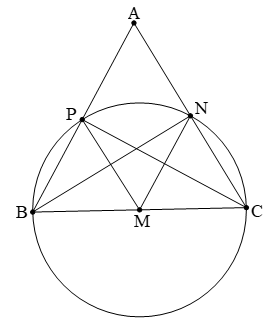
5. Ví dụ cụ thể

Câu 1: Cho tam giác đều ABC có cạnh bằng a. AB, BN, CP là các đường trung tuyến. Chứng minh 4 điểm B, P, N, C cùng thuộc một đường tròn. Tính bán kính đường tròn đó.

Hướng dẫn:

Vì tam giác ABC đều nên các trung tuyến đồng thời cũng là đường cao .

Suy ra AM, BN, CP lần lượt vuông góc với BC, AC, AB.

Từ đó ta có các tam giác BPC, BNC là tam giác vuông với BC là cạnh huyền

Tam giác BPC vuông tại P có đường trung tuyến PM nên PM = BM = MC = 1/2 BC (1)

Tam giác BNC vuông tại N có đường trung tuyến NM nên NM = MB = MC = 1/2 BC (2)

Từ (1) và (2) suy ra: PM = NM = MB = MC = 1/2 BC

Hay: Các điểm B, P, N, C cùng thuộc đường tròn

Đường kính BC = a, tâm đường tròn là trung điểm M của BC

Câu 2: Cho tứ giác ABCD có ∠C + ∠D = 90°. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó .

Hướng dẫn:

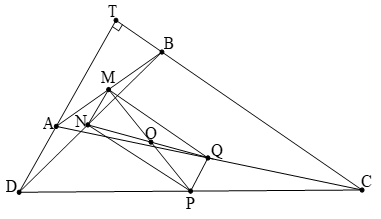
Kéo dài AD, CB cắt nhau tại điểm T thì tam giác TCD vuông tại T.

    + Do MN là đường trung bình của tam giác ABD nên NM // AD

    + MQ là đường trung bình của tam giác ABC nên MQ // BC. Mặt khác AD ⊥ BC ⇒ MN ⊥ MQ.

Chứng minh tương tự ta cũng có: MN ⊥ NP, NP ⊥ PQ. Suy ra MNPQ là hình chữ nhật.

Hay các điểm M, N, P, Q thuộc một đường tròn có tâm là giao điểm O của hai đường chéo NQ, MP

B. Bài tập tự luận

Câu 1: Chứng minh rằng đường tròn ngoại tiếp tam giác vuông có tâm chính là trung điểm của cạnh huyền

Lời giải:

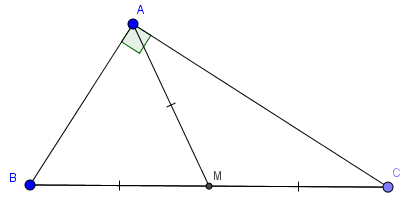
Xét tam giác ABC vuông tại A

Gọi M là trung điểm của BC.

Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông ta có:

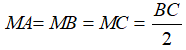
Đường tròn ngoại tiếp tam giác ABC có tâm là trung điểm của cạnh huyền

Câu 2: Cho hình chữ nhật ABCD có AB = 10, BC = 8 . Chứng minh rằng A, B, C, D cùng thuộc một đường tròn và tính bán kính của đường tròn đó

Lời giải:

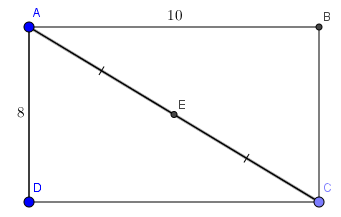
Gọi E là giao điểm của AC và BD.

Theo tính chất hai đường chéo trong hình chữ nhật ta có:

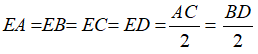
Khi đó A, B, C, D cùng thuộc đường tròn tâm E và bán kính EA

Ta có: