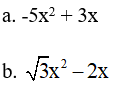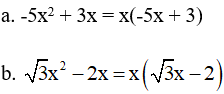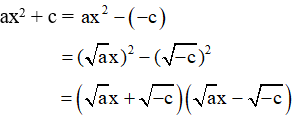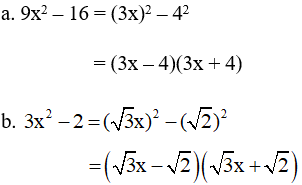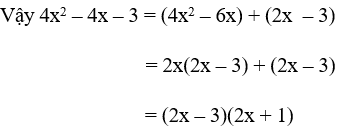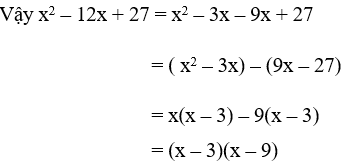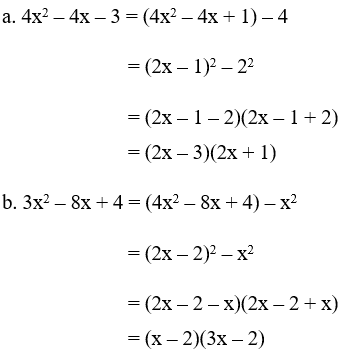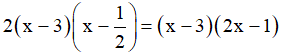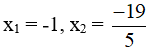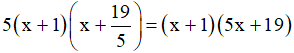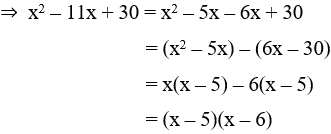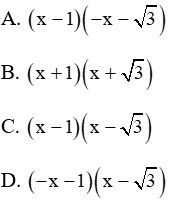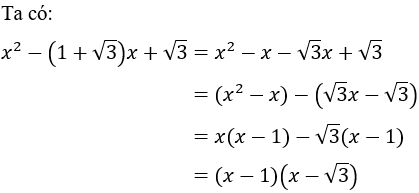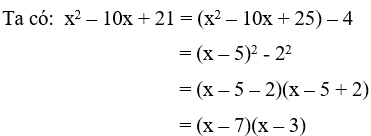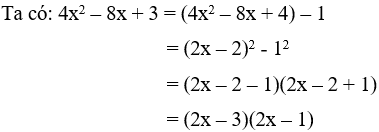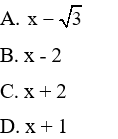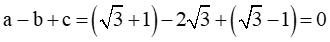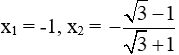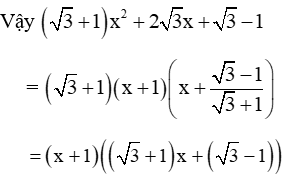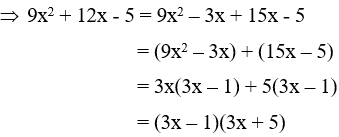Cách phân tích đa thức ax^2 + bx + c thành nhân tử để giải phương trình bậc hai | Toán lớp 9

Cách phân tích đa thức ax^2 + bx + c thành nhân tử để giải phương trình bậc hai

Với Cách phân tích đa thức ax^2 + bx + c thành nhân tử để giải phương trình bậc hai Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phân tích đa thức ax^2 + bx + c thành nhân tử để giải phương trình bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Cách 1: Đặt nhân tử chung

- Sử dụng trong trường hợp c = 0, khi đó ta có ax² + bx = x(ax + b)

Ví dụ: Phân tích biểu thức sau thành nhân tử

Giải

Cách 2: Dùng hằng đẳng thức A² – B²

- Sử dụng trong trường hợp b = 0 và c < 0, khi đó ta có:

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 9x² – 16

b. 3x² – 2

Giải

Cách 3: Tách số hạng bx thành hai số hạng rồi nhóm các hạng tử và đặt nhân tử chung

-bổ sung- Để tách bx thành hai hạng tử ta làm như sau:

+ B1: Tìm tích ac, phân tích ac thành tích hai thừa số nguyên

+ B2: Chọn hai thừa số có tổng bằng b

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 4x² – 4x - 3

b. x² – 12x + 27

Giải

a. Tích ac = -12 = (-1).12 = (-12).1 = 2.(-6) = (-2).6

Trong các cặp số trên ta chọn cặp số 2 và -6 vì tổng của chúng bằng -4 = b

⇒ -4x = -6x + 2x

b. Tích ac = 27 = 1.27 = (-1).(-27) = 3.9 = (-3).(-9)

Trong các cặp số trên ta chọn cặp số -3 và -9 vì tổng của chúng bằng -12 = b

⇒ -12x = -3x - 9x

Cách 4: Tách số hạng (ax² hoặc c) thành hai số hạng rồi đưa biểu thức

ax² + bx +c về dạng A² – B²

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 4x² – 4x – 3

b. 3x² – 8x + 4

Giải

Cách 5: Sử dụng nghiệm của phương trình bậc hai

- Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì:

ax² + bx + c = a(x – x₁)(x – x₂)

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 2x² – 7x + 3

b. 5x² + 24x + 19

Giải

a. Xét phương trình 2x² – 7x + 3 = 0 có: Δ = b² - 4ac = (-7)² - 4.2.3 = 25 > 0

Do đó phương trình có 2 nghiệm phân biệt: x₁ = 3, x₂ = 1/2

Vậy 2x² – 7x + 3 =

b. Xét phương trình 5x² + 24x + 19 = 0 có: Δ = b² - 4ac = (24)² - 4.5.19 = 196 > 0

Do đó phương trình có 2 nghiệm phân biệt: x₁ = -1, x₂ =

Vậy 5x² + 24x + 19 =

B. Bài tập

Câu 1: Khi phân tích biểu thức x² – 11x + 30 thành nhân tử ta được kết quả là

A. (x – 5)(x – 6)

B. (x + 5)(x + 6)

C. (x – 3)(x – 10)

D. (x – 2)(x – 15)

Giải

Tích ac = 30 = (-5).(-6) = 5.6 = 2.15 = (-2).(-15) = 3.10 = (-3).(-10)

Trong các cặp số trên ta chọn cặp số -5 và -6 vì tổng của chúng bằng -11 = b

Đáp án A

Câu 2: Khi phân tích biểu thức 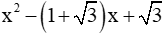thành nhân tử ta được kết quả là

Giải

Đáp án C

Câu 3: Khi phân tích biểu thức x² – 10x + 21thành (x + a)(x + b) thì tổng của a và b bằng bao nhiêu

A. -9

B. -10

C. -11

D. -12

Giải

Vậy a + b = -7 – 3 = -10

Đáp án B

Câu 4: Khi phân tích biểu thức 4x² – 8x + 3 thành (ax + b)(cx + d) thì tích của b và d bằng bao nhiêu

A. 1

B. 2

C. 3

D. 4

Giải

Vậy tích bd = (-3).(-1) = 3

Đáp án C

Câu 5: Khi phân tích biểu thức 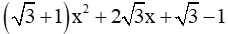thành nhân tử thì một trong hai nhân tử là

Giải

Xét phương trình 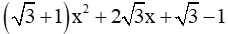= 0 có:

Do đó phương trình có 2 nghiệm phân biệt:

Vậy đáp án D

Câu 6: Khi phân tích biểu thức 9x² + 12x - 5 thành nhân tử thì một trong hai nhân tử là

A. x - 7

B. x - 2

C. 3x + 2

D. 3x + 5

Giải

Tích ac = -45 = (-5).9 = 5.(-9) = (-3).15 = 3.(-15) = 1.(-45) = (-1).45

Trong các cặp số trên ta chọn cặp số -3 và 15 vì tổng của chúng bằng 12 = b

Đáp án D

Câu 7: Kết quả phân tích biểu thức x² + 7x + 12 thành nhân tử là

A. (x + 1)(x + 12)

B. (x + 3)(x + 4)

C. (x - 3)(x - 4)

D. (x - 1)(x - 12)

Giải

Xét phương trình x² + 7x + 12 = 0

Phương trình có ∆ = 7² – 4.1.12 = 49 – 48 = 1 > 0 nên có hai nghiệm phân biệt

⇒ x² + 7x + 12 = (x + 3)(x + 4)

Đáp án B

Câu 8: Biểu thức nào sau đây có kết quả phân tích thành nhân tử là (3x – 2)(-x + 7)

A. -3x² + 13x - 14

B. -3x² + 33x - 14

C. -3x² + 23x - 14

D. -3x² + 3x - 14

Giải

Ta có (3x – 2)(-x + 7) = -3x² + 21x + 2x -14 = -3x² + 23x - 14

Đáp án C