Cách giải bài toán cấu tạo số cực hay | Giải bài toán bằng cách lập hệ phương trình | Toán lớp 9
Cách giải bài toán cấu tạo số cực hay | Giải bài toán bằng cách lập hệ phương trình
Với Cách giải bài toán cấu tạo số cực hay | Giải bài toán bằng cách lập hệ phương trình Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bài toán cấu tạo số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
Phương pháp giải:
Bước 1: Lập hệ phương trình:
● Đặt ẩn và tìm điều kiện của ẩn (nếu có).
● Biểu diễn cácđại lượng chưa biết theo ẩn và các đại lượng đã biết.
● Lập hệ phương trình biểu diễn tương quan giữa các đại lượng.
Bước 2: Giải hệ phương trình.
Bước 3: So sánh với điều kiện và kết luận.
B. Ví dụ minh họa
Ví dụ 1: Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 1006 và nếu lấy số lớn chia số nhỏ thì được thương là 2 và số dư là 124.
Hướng dẫn:
Gọi hai số cần tìm là a và b (giả sử a > b), a,b > 0
Theo bài ra, tổng của hai số đó là 1006 ta có: a + b = 1006.
Lấy số lớn chia cho số nhỏ thì được thương là 2 và dư 124 ta có: a = b.2 + 124
Ta có hệ phương trình: 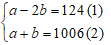
Lấy pt (2) trừ pt (1) ta được: 3b = 882 ⇒ b = 294 (thỏa mãn)
Với b = 294 ⇒ a = 1006 – 294 = 712.(thỏa mãn)
Vậy hai số cần tìm là 712 và 294.
Ví dụ 2: Tổng của hai số bằng 59. Hai lần số này bé hơn ba lần số kia là 7. Tìm hai số đó?
Hướng dẫn:
Gọi hai số cần tìm là x và y ( )
Theo bài ra, tổng hai số là 59 ta có: x + y = 59
Vì hai lần số này bé hơn ba lần số kia là 7 nên ta có: 3x – 2y = 7
Ta có hệ phương trình: 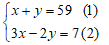
Nhân pt (1) với 2, rồi cộng với pt (2) ta được: 5x = 125 ⇒ x = 25 (thỏa mãn)
Với x = 25 ⇒ y = 34 (thỏa mãn)
Vậy hai số cần tìm là: 34 và 25.
Ví dụ 3: Cho một số có hai chữ số. Nếu đổi chỗ hai số của nó thì ta được số mới lớn hơn số đã cho là 63. Tổng của số đã cho và số mới tạo thành bằng 99. Tìm số đó?
Hướng dẫn:
Gọi số có hai chữ số là 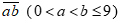
Vì đổi chỗ hai số của số ban đầu thì được số mới lớn hơn số ban đầu là 63 ta có: 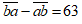
Tổng của số ban đầu và số mới là 99 nên ta có: 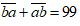
Ta có hệ phương trình: 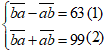
Lấy pt (1) cộng pt (2) ta được: 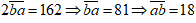
Vậy số cần tìm là 18.

C. Bài tập trắc nghiệm
Câu 1: Tổng của hai số là số lớn nhất có 3 chữ số chia hết cho 2. Biết nếu thêm vào số bé 42 đơn vị thì ta được số lớn. Tìm mỗi số?
A. Số lớn = 520, số bé = 478.
B. Số lớn = 620, số bé = 378.
C. Số lớn = 820, số bé = 78.
D. Số lớn = 720, số bé = 278.
Lời giải:
Hướng dẫn:
Gọi hai số cần tìm lần lượt là x, y (giả sử x > y), ( )
Số lớn nhất có 3 chữ số chia hết cho 2 là 998.
Tổng của hai số là số lớn nhất có 3 chữ số chia hết cho 2 nên ta có: x + y = 998.
Vì thêm vào số bé 42 đơn vị thì ta được số lớn nên ta có: y + 42 = x
Ta có hệ phương trình: 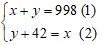
Thay x = y + 42 vào pt (1) ta được: y + 42 + y = 998 ⇔ 2y = 956 ⇒ y = 478(thỏa mãn)
Với y = 478 ⇒ x = 478 + 42 = 520 (thỏa mãn)
Vậy hai số cần tìm là 520 và 478.
Chọn đáp án A.
Câu 2: Tìm hai số có hiệu là số tự nhiên bé nhất có hai chữ số chia hết cho 5 và tổng là số tự nhiên lớn nhất có hai chữ số chia hết cho 2 .(x , y nguyên dương)
A. Số lớn = 60, số bé = 38.
B. Số lớn = 54, số bé = 44.
C. Số lớn = 80, số bé = 18.
D. Số lớn = 72, số bé = 26.
Lời giải:
Hướng dẫn:
Gọi hai số cần tìm lần lượt là x, y (giả sử x > y),
Số bé nhất có hai chữ số chia hết cho 5 là 10.
Số lớn nhất có hai chữ số chia hết cho 2 là 98
Vì hiệu của hai số là số bé nhất có hai chữ chia hết cho 5 ta có: x – y = 10
Vì tổng của hai số là số lớn nhất có hai chữ số chia hết cho 2 ta có: x + y = 98
Ta có hệ phương trình: 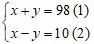
Cộng vế theo vế pt (1) và pt (2) ta được: 2x = 108 ⇒ x = 54 (thỏa mãn)
Với x = 54 ⇒ y = 98 – 54 = 44 (thỏa mãn)
Vậy hai số cần tìm là 54 và 44.
Chọn đáp án B.
Câu 3: Tìm tất cả các số tự nhiên có hai chữ số, biết rằng chữ số hàng đơn vị nhỏ hơn chữ số hàng chục là 2 và tích của hai chữ số của nó luôn lớn hơn tổng hai chữ số của nó là 34.
A. 38.
B. 83
C. 86
D. 68
Lời giải:
Hướng dẫn:
Gọi số có hai chữ số là 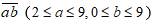
Vì chữ số hàng đơn vị nhỏ hơn chữ số hàng chục là 2, ta có: a – b = 2
Vì tích của hai chữ số của nó luôn lớn hơn tổng hai chữ số của nó là 34, ta có: ab – (a + b) = 34
Ta có hệ phương trình: 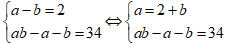
Thay a = 2 + b vào pt (2) ta được:
(2 + b)b – (2 + b) – b = 34 ⇔ 2b + b2 – 2 – b – b = 34 ⇔ b2 = 36
Với b = 6 ⇒ a = 8 (thỏa mãn)
Với b = – 6 (loại)
Vậy số cần tìm là 86.
Chọn đáp án C.
Câu 4: Cho một số có hai chữ số, biết rằng tổng của hai chữ số của nó bằng 8 và hiệu hai chữ số của nó bằng 2,(biết chữ số hàng chục lớn hơn chữ số hàng đơn vị). Khẳng định nào sau đây đúng?
A. Số cần tìm lớn hơn 60.
B. Số cần tìm nhỏ hơn 40.
C. Số cần tìm 54.
D. Số cần tìm là 53.
Lời giải:
Hướng dẫn:
Gọi số có hai chữ số là 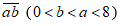
Vì tổng của hai chữ số của nó bằng 8, ta có: (a + b) = 8
Vì hiệu hai chữ sô của nó bằng 2 nên ta có: a – b = 2
Ta có hệ phương trình: 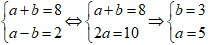
Vậy số cần tìm là 53.
Chọn đáp án D.
Câu 5: Cho một số có hai chữ số, biết rằng nếu chia số đó cho tổng của hai chữ số của nó được thương là 6 và hiệu của hai chữ số đó bằng 1. Khẳng định nào sau đây đúng?
A. Số cần tìm lớn hơn 60.
B. Số cần tìm nhỏ hơn 40.
C. Số cần tìm có tổng hai chữ số bằng 9.
D. Số cần tìm có tổng hai chữ số bằng 7.
Lời giải:
Hướng dẫn:
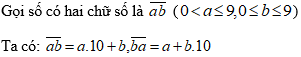
Vì chia số đó cho tổng của hai chữ số của nó được thương là 6, nên ta có: 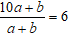
Vì: hiệu hai chữ số đó bằng 1, ta có: a – b = 1
Ta có hệ phương trình:
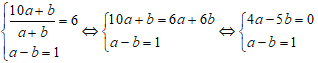
Từ pt (2) ta có: a = 1 + b vào pt (1) ta được: 4(1 + b) – 5b = 0 ⇒ b = 4
Với b = 4 ⇒ a = 5.
Vây số cần tìm là 54.
Chọn đáp án C.

Câu 6: Tìm hai số biết hiệu của hai số đó bằng 1275 và nếu lấy số lớn hơn chia cho số bé thì được thương là 3 dư 125. Khẳng định nào sau đây đúng?
A. Số lớn = 1850, số bé = 575.
B. Số lớn = 1575, số bé = 700.
C. Số lớn = 1680, số bé = 595.
D. Số lớn = 1720, số bé = 555.
Lời giải:
Hướng dẫn:
Gọi hai số cần tìm lần lượt là x, y (giả sử x > y), ( )
Vì hiệu của hai số đó bằng 1275 nên ta có: x – y = 1275
Vì số lớn hơn chia cho số bé thì được thương là 3 dư 125, ta có: x = 3y + 125
Ta có hệ phương trình: 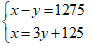
Thay x = 3y + 125 vào pt (1) ta được: 3y + 125 – y = 1275 ⇒ 2y = 1150 ⇒ y = 575 (tm)
Với y = 575 ⇒ x = 1850.
Vậy hai sô cần tìm là 1850 và 575.
Chọn đáp án A.
Câu 7: Cho một số có hai chữ số, biết rằng tổng của hai chữ số của nó là 16 và nếu đổi chỗ hai chữ số cho nhau thi được số mới nhỏ hơn số đã cho 18 đơn vị. Khẳng định nào sau đây đúng?
A. Số cần tìm nhỏ hơn 60.
B. Số cần tìm là 79
C. Số cần tìm có tổng hai chữ số bằng 14.
D. Số cần tìm có tổng hai chữ số bằng 12.
Lời giải:
Hướng dẫn:
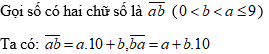
Vì tổng của hai chữ số của nó là 16, nên ta có: a + b = 16
Vì đổi chỗ hai chữ số cho nhau thi được số mới nhỏ hơn số đã cho 18 đơn vị, ta có:
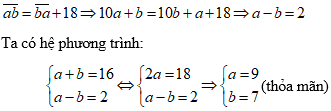
Vậy số cần tìm là 97.
Chọn đáp án B.
Câu 8: Cho một số có hai chữ số. Nếu đổi chỗ hai số của nó thì ta được số mới lớn hơn số đã cho là 36. Tổng của số đã cho và số mới tạo thành bằng 110. Tìm số đó?
A. 63
B. 38
C. 37
D. 73
Lời giải:
Hướng dẫn:
Gọi số có hai chữ số là 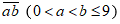
Vì đổi chỗ hai số của số ban đầu thì được số mới lớn hơn số ban đầu là 36 ta có: 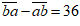
Tổng của số ban đầu và số mới là 110 nên ta có: 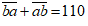
Ta có hệ phương trình: 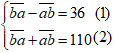
Lấy pt (1) cộng pt (2) ta được: 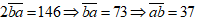
Vậy số cần tìm là 37.
Chọn đáp án C.
Câu 9: Tìm hai số, biết rằng bốn lần số thứ hai cộng với năm lần số thứ nhất bằng 18040 và ba lần số thứ nhất hơn hai lần số thứ hai là 2002.
A. Số lớn = 1150, số bé = 1565.
B. Số lớn = 3570, số bé = 2240.
C. Số lớn = 2680, số bé = 2420.
D. Số lớn = 2005, số bé = 2004.
Lời giải:
Hướng dẫn:
Gọi hai số cần tìm lần lượt là x, y
Vì bốn lần số thứ hai cộng với năm lần số thứ nhất bằng 18040, nên ta có: 5x + 4y =18040
Vì ba lần số thứ nhất hơn hai lần số thứ hai là 2002, ta có: 3x – 2y = 2002.
Ta có hệ phương trình: 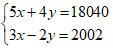
Nhân pt (2) với 2, rồi cộng với pt (1) ta được: 11x = 22044 ⇒ x = 2004
Với x = 2004 ⇒ y = (3. 2004 – 2002) : 2 = 2005.
Vậy hai số cần tìm là 2005 và 2004.
Chọn đáp án D.
Câu 10: Tìm số có hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5 và đem số đó chia cho tổng hai chữ số thì được thương là 7 và dư 6.
A. 38.
B. 83
C. 86 D.68
Lời giải:
Hướng dẫn:
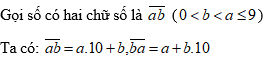
Vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5, ta có: a – b = 5.
Vì đem số đó chia cho tổng hai chữ số thì được thương là 7 và dư 6, ta có:
10a + b = 7 (a + b) + 6. (thỏa mãn)
Ta có hệ pt: 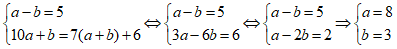
Vậy số cần tìm là 83.
Chọn đáp án B.

