Tổng hợp lý thuyết Chương 4 Hình học 9 hay, chi tiết | Toán lớp 9

Tổng hợp lý thuyết Chương 4 Hình học 9 hay, chi tiết

Tài liệu Tổng hợp lý thuyết Chương 4 Hình học 9 hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Chương 4 Hình học từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Hình trụ.

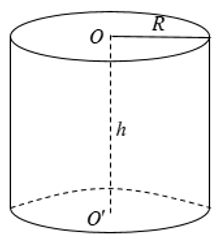
Cho hình trụ có bán kính đáy R và chiều cao h.

    + Diện tích xung quanh: S_xq = 2πRh

    + Diện tích toàn phần: S_tp = 2πRh + 2πR²

    + Thể tích: V = πR²h

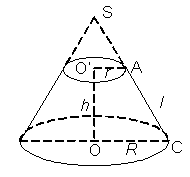
2. Hình nón – Hình nón cụt

a) Hình nón

Đặt AC = l; l là đường sinh

Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.

    + Diện tích xung quanh: S_xq = πRl

    + Diện tích toàn phần: S_tp = πRl + πR²

    + Thể tích: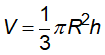

b) Hình nón cụt

Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.

    + Diện tích xung qaunh: S_xq = π(R + r)l

    + Thể tích: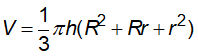

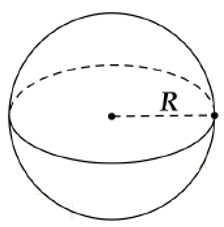
3. Hình cầu

Cho hình cầu bán kính R.

    + Diện tích mặt cầu: S = 4πR²

    + Thể tích hình cầu: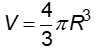

B. Bài tập tự luận

Câu 1: Một hình trụ có bán kính đáy bằng 1/4 đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là một hình chữ nhật có diện tích là 50cm². Tính diện tích xung quanh và thể tích hình trụ.

Lời giải:

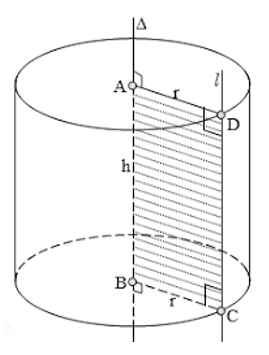
Theo giả thiết ta có

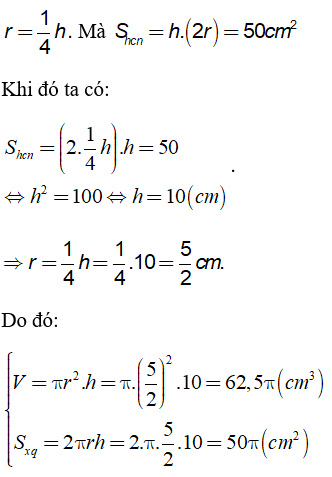
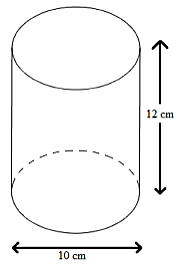
Câu 2: Tính diện tích xung quanh và diện tích toàn phần của hình sau

Lời giải:

Câu 3: Hình chữ nhật ABCD có AB = a, BC = 3a . Quay hình chữ nhật quanh cạnh AB thì được thể tích V₁, quay quanh cạnh BC thì được thể tích V₂. Tỉ số thể tích giữa V₁ và V₂ là?

Lời giải:

Câu 4: Cho hình nón như hình bên:

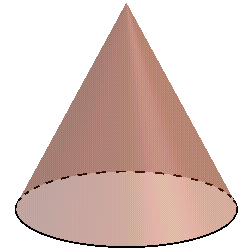
Biết rằng đáy là hình tròn có bán kính bằng 3cm, đường sinh có độ dài là 5cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón đó.

Lời giải:

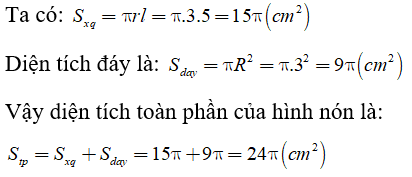
Muốn tính thể tích hình nón, ta cần biết chiều cao hạ từ đỉnh xuống đáy (hay khoảng cách từ đỉnh xuống tâm đường tròn)

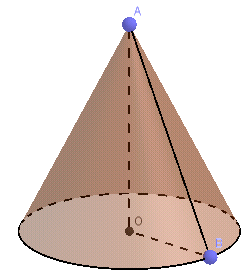
Xét tam giác AOB vuông tại O

Áp dụng định lý Pi – ta- go trong tam giác AOB ta có:

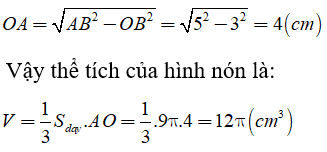
Câu 5: Cho hình nón cụt như hình vẽ

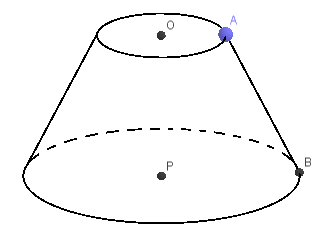
Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh và thể tích của hình nón cụt

Lời giải:

Diện tích xung quanh của hình nón cụt là:

S_xq = π(r + R)l = π(3 + 6).4 = 36π (cm²)

Để tính chiều cao hình nón cụt, ta có hình vẽ sau:

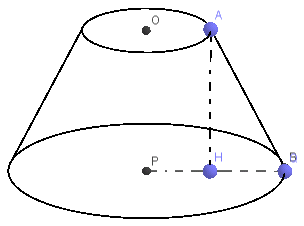
Áp dụng định lý Py – ta – go và tam giác AHB vuông tại H ta có:

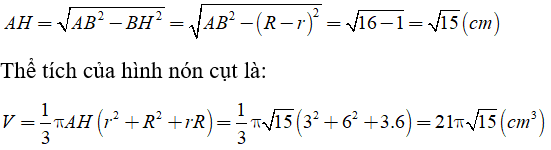
Câu 6: Khi bán kính của một mặt cầu tăng lên 3/2 lần thì diện tích và thể tích thay đổi như thế nào?

Lời giải:

Theo công thức diện tích ta có: S = 4πR²

Dựa vào công thức trên, khi tăng R lên 3/2 lần thì diện tích tăng lên R² tức là 9/4 lần

Tương tự đối với thể tích: V = 4/3 πR³

Dựa vào công thức trên, khi tăng R lên 3/2 lần thì thể tích tăng lên R³ tức là 27/8 lần.

Câu 7: Giả sử trái cam có hình tương tự như mặt cầu, bạn Lan cắt trái cam làm đôi và tiến hành đo đường kính của nửa trái cam vừa cắt, bạn đo được bán kính tính cả vỏ cam là 2,5cm, biết vỏ cam dày 3mm. Hãy tính thể tích thực của quả cam đó.

Lời giải:

Xem như phần cam đã mà Lan đã ăn cũng là một dạng mặt cầu, vậy bán kính của mặt cầu ấy chính là bán kính của quả cam đó trừ đi vỏ.

Câu 8: Mô tả hình dưới đây được tạo bởi một hình nón có đường sinh bằng 13cm, bán kính là 5cm và một nửa mặt cầu. Hãy tính thể tích khối hình

Lời giải:

Dễ dàng tính được đường cao của hình nón bằng định lý Py – ta – go:

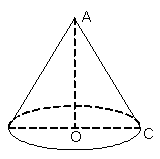
Câu 9: Hình bên mô tả chiếc nón của một chú hề được tạo bởi hình chóp và hai đường tròn đồng tâm. Biết rằng hình tròn nhỏ bỏ trống để chú hề có thể đội được nón.

Cho AB = 10cm, OB = 6cm, OC = 9cm. Tính diện tích để làm chiếc nón ấy

Lời giải:

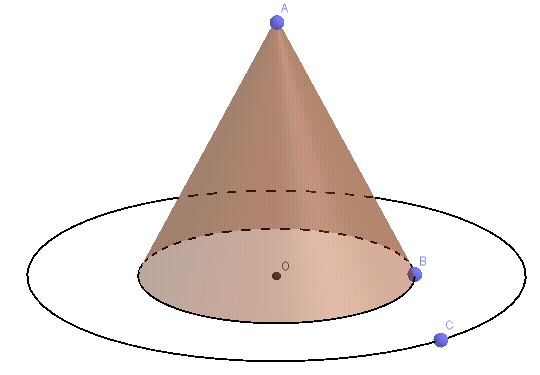
Ta thấy chiếc nón chính là diện tích toàn phần của hình nón và phần diện tích hình nón lớn trừ diện tích hình nón nhỏ

Câu 10: Mọt hình nón được một mặt phẳng cắt ngang song song với đáy tại trung điểm của đường cao, hình nón được chia ra làm thành một hình nón cụt và một hình nón. Tính tỷ lệ của hình nón mới với hình nón cụt vừa tạo ra?

Lời giải:

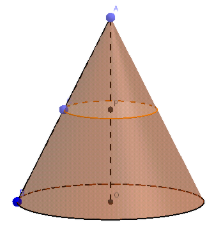
Ở hình bên, ta có P là trung điểm của OA, C là trung điểm của AB

Dễ dàng suy ra được trong hình nón cụt, đáy lớn có bán kính gấp đôi đáy bé

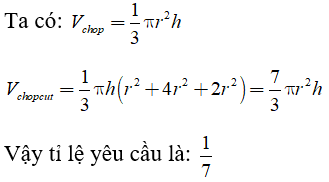
Câu 11: Hình bên là hình được ghép bởi một hình nón và một hình trụ, để hai hình này có thể tích bằng nhau thì chiều cao của hình nón phải bằng bao nhiêu lần chiều cao của hình trụ?

Lời giải:

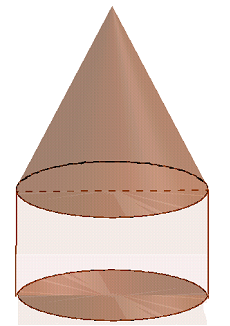
Vậy để hai thể tích này bằng nhau thì chiều cao của hình nón phải bằng 3 lần chiều cao của hình trụ