Bài tập trắc nghiệm Chương 1 Đại Số 9 chọn lọc, có đáp án | Toán lớp 9 | Toán lớp 9

Bài tập trắc nghiệm Chương 1 Đại Số 9 chọn lọc, có đáp án | Toán lớp 9

Với Bài tập trắc nghiệm Chương 1 Đại Số 9 chọn lọc, có đáp án | Toán lớp 9 Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 1 Đại Số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

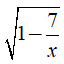
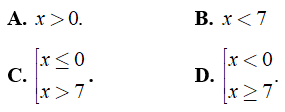
Câu 1: Biểu thức có nghĩa khi ?

Lời giải:

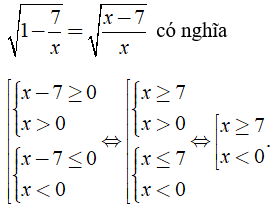
Chọn đáp án D.

Câu 2: Biểu thức 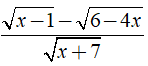có nghĩa khi ?

A. x < 1        B. x ≥ 3/2        C. 1 ≤ x ≤ 3/2        D. x ≥ -7

Lời giải:

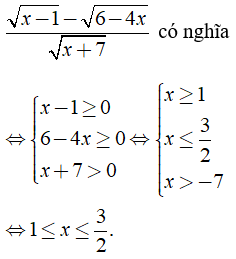
Chọn đáp án C.

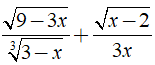
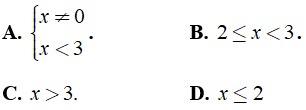
Câu 3: Biểu thức có nghĩa khi ?

Lời giải:

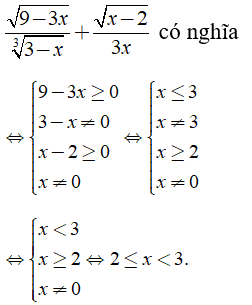
Chọn đáp án B.

Câu 4: Biểu thức 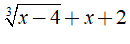có nghĩa khi ?

A. x ∈ R        B. x > 4        C. x ≤ 4        D. x ∈ R\{4}

Lời giải:

- Vì biểu thức trong căn bậc ba luôn tồn tại với mọi x ∈ R

Nên 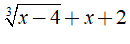có nghĩa với mọi x ∈ R

Chọn đáp án A.

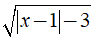
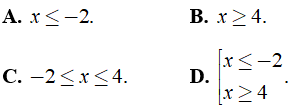
Câu 5: Biểu thức có nghĩa khi ?

Lời giải:

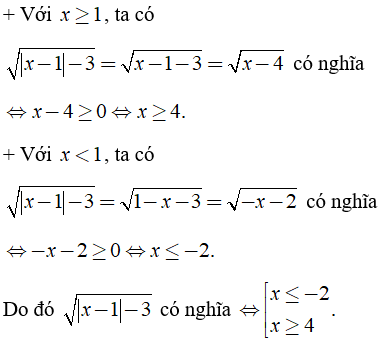
Chọn đáp án D.

Câu 6: Kết quả của phép tính 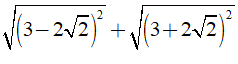là?

A. 6        B. 4√2        C. -4√2        D. -6

Lời giải:

Ta có

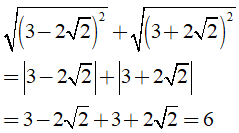
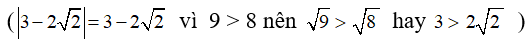
Chọn đáp án A.

Câu 7: Kết quả của phép tính 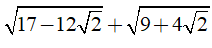là ?

A. 2        B. -4        C. 4        D. √2

Lời giải:

Ta có:

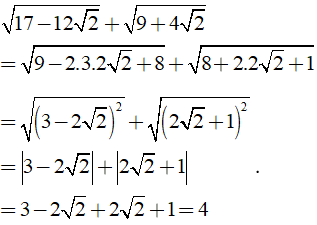
Chọn đáp án C.

Câu 8: Kết quả của phép tính 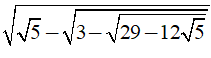là ?

A. √5        B. 2√5        C. 0        D. 1

Lời giải:

Ta có

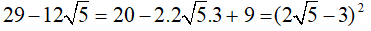
Nên:

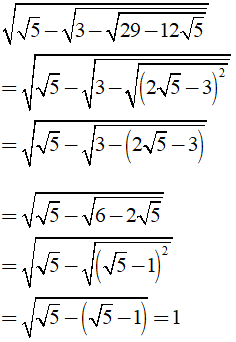
Chọn đáp án D.

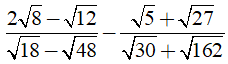
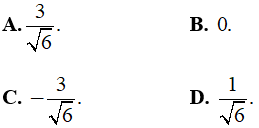
Câu 9: Kết quả của phép tính là ?

Lời giải:

Ta có:

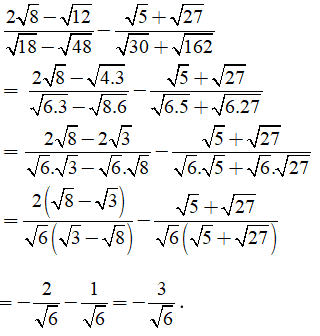
Chọn đáp án C.

Câu 10: Kết quả của phép tính 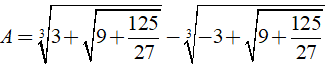là ?

A. A = 1        B. A = -1        C. A = √2        D. A = 0

Lời giải:

Đặt:

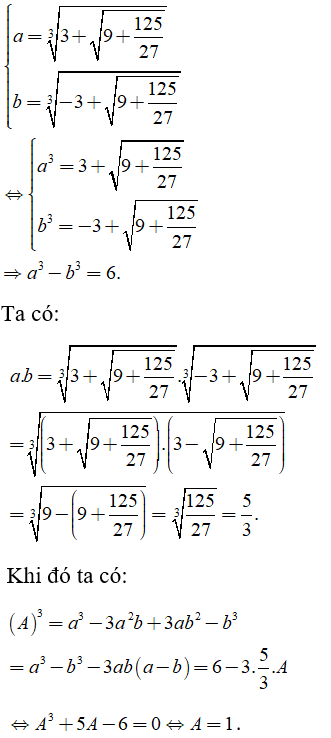
Chọn đáp án A.

Câu 11: Phương trình √x = a vô nghiệm khi ?

A. a = 0        B. a > 0        C. a < 0        D. a ≠ 0

Lời giải:

Phương trình √x = a có nghiệm ⇔ a ≥ 0

⇒ Đáp án A, B sai

    + Với a ≠ 0 ta vẫn có thể xảy ra trường hợp a > 0 nên với a ≠ 0 phương trình có nghiệm.

⇒ Với a < 0 phương trình √x = a vô nghiệm.

Chọn đáp án C.

Câu 12: Căn bậc hai số học của 9 là ?

A. 3        B. -3        C. ±3        D. 81

Lời giải:

Ở đây, ta phải nhớ: số a không âm thì chỉ có một căn bậc hai số học và số a đó có hai căn bậc hai là ±√a.

Căn bậc hai số học của 9 là 3 và 3 > 0; 3² = 9

Chọn đáp án A.

Câu 13: So sánh 9 với √79, ta được kết luận đúng nào ?

A. 9 < √79        B. 9 = √79

C. 9 > √79        D. Không so sánh được

Lời giải:

Ta có 81 > 79 ⇒ √81 > √79 ⇒ 9 > √79

Chọn đáp án C.

Câu 14: Rút gọn biểu thức 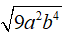bằng ?

A. 3ab²        B. 3a²b        C. 3|a|b²        D. 3a|b²|

Lời giải:

Ta có:

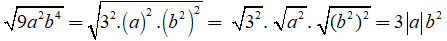
(Vì chưa có điều kiện của a và b² ≥ 0 ∀ b)

Chọn đáp án C.

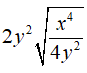
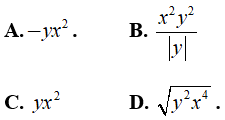
Câu 15: Biểu thức với y < 0 được rút gọn là ?

Lời giải:

Ta có:

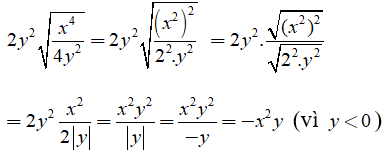
Chọn đáp án A.

Câu 16: Rút gọn biểu thức 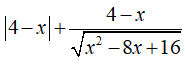với x < 4 là ?

A. 5 - x        B. 3 - x        C. 3 + x        D. x - 4

Lời giải:

Ta có:

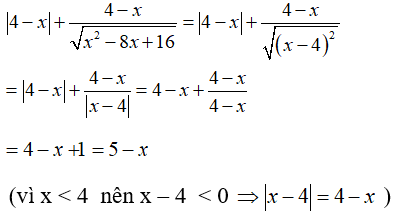
Chọn đáp án A.

Câu 17: Nếu 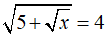thì giá trị của x là ?

A. x = 11        B. x = -1        C. x = 121        D. x = 4

Lời giải:

Điều kiện: x ≥ 0

Ta có:

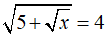
⇔ 5 + √x = 16

⇔ √x = 11 ⇔ x = 121

Chọn đáp án C.

Câu 18: Giá trị của x để 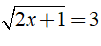là?

A. x = 2        B. x = 4        C. x = 13        D. x = 11

Lời giải:

Điều kiện: x ≥ -1/2

Ta có:

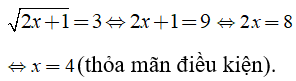
Chọn đáp án B.

Câu 19: Nếu 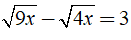thì giá trị của x là ?

A. x = 3        B. x = 9/5        C. x = 9        D. x = 4

Lời giải:

Điều kiện: x ≥ 0

Ta có:

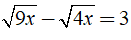
⇔ 3√x - 2√x = 3

⇔ √x = 3 ⇔ x = 9

Kết hợp điều kiện ta được x = 9.

Chọn đáp án C.

Câu 20: Giá trị của biểu thức 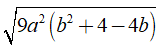khi a = 2 và b = -√3, bằng giá trị nào sau đây ?

A. 6(2 + √3)        B. 6(2 - √3)

C. 3(2 + √3)        D. 3(2 - √3)

Lời giải:

Ta có

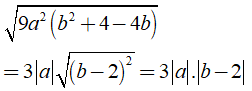
Với a = 2 và b = -√3, ta có:

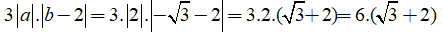
Chọn đáp án A.

Câu 21: Giá trị của x để biểu thức 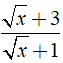nhận giá trị nguyên?

A. {1; 2}        B. {0; 1}        C. {2; 4}        D. {0; 4}

Lời giải:

Điều kiện: x ≥ 0

Ta có:

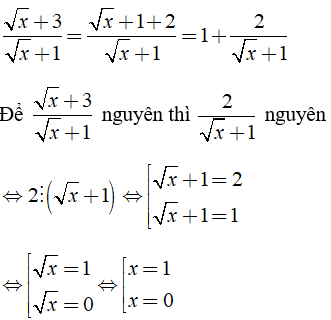
Chọn đáp án B.

Câu 22: Giá trị nhỏ nhất của biểu thức 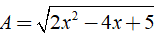là ?

A. 3        B. 1        C. √3        D. √2

Lời giải:

Ta có:

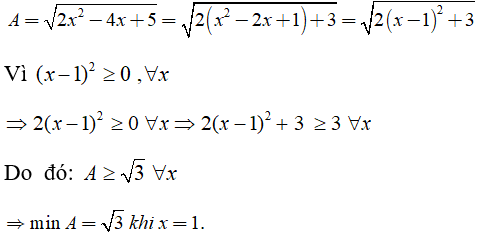
Chọn đáp án C.

Câu 23: Cho phương trình 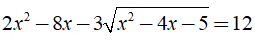, nhận xét nào sau đây đúng ?

A. Phương trình có hai nghiệm x₁, x₂ thỏa mãn x₁ + x₂ = 5

B. Phương trình có hai nghiệm x₁, x₂ thỏa mãn x₁.x₂ = -9

C. Nghiệm của phương trình đã cho thỏa mãn x ∈ [-1; 5]

D. Phương trình có hai nghiệm x₁, x₂ thỏa mãn x₁ - 9/x₂ = 4

Lời giải:

Điều kiện:

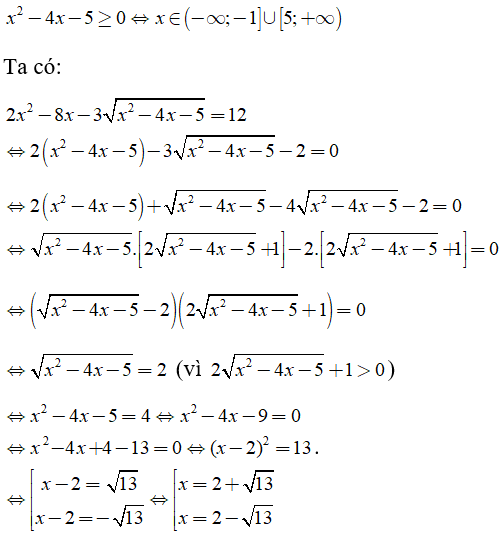
Kết hợp điều kiện ta thấy hai giá trị trên đều thỏa mãn điều kiện.

Khi đó ta có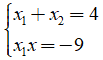

Chọn đáp án B.

Câu 24: Kết quả của rút gọn biểu thức

là?

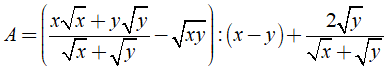
A. A = 1        B. A = √x + √y

C. A = √x - √y        D. A = 2√y

Lời giải:

Điều kiện: x ≥ 0; y ≥ 0; x + y > 0

Ta có:

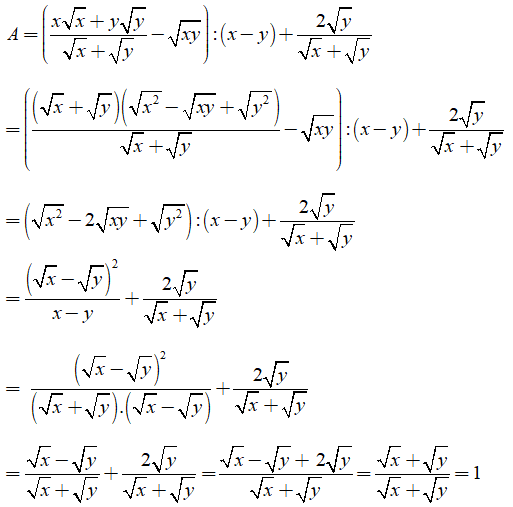
Vậy A = 1

Chọn đáp án A.

Câu 25: Cho biểu thức

(với x ≥ 0; x ≠ 1 và x ≠ 1/4).

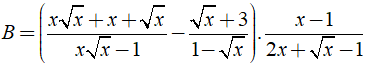
Tìm giá trị của x để B < 0.

A. 0 < x < 1/4        B. 0 ≤ x < 1/4

C. x > 1/4        D. x ≤ 0

Lời giải:

Ta có:

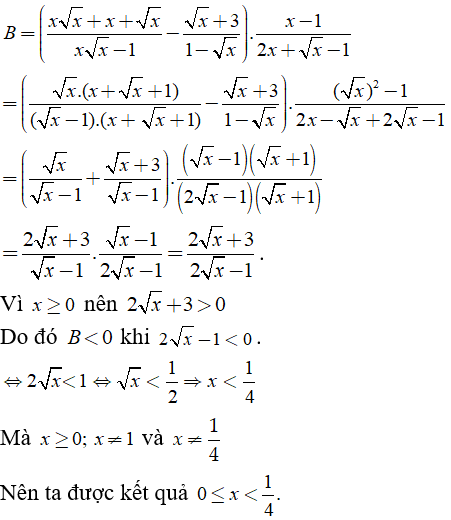
Chọn đáp án B.

Câu 26: Cho biểu thức

A =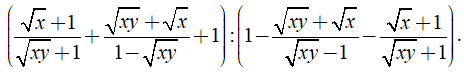

Nếu 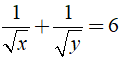thì Max A bằng ?

A. 9        B. 3        C. 36        D. 18

Lời giải:

Điều kiện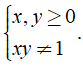

Ta có:

Chọn đáp án A.

Câu 27: Cho biểu thức 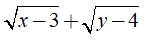biết x + y = 8. Giá trị lớn nhất của biểu thức là ?

A. 1        B. √2        C. √3        D. √5

Lời giải:

Áp dụng BĐT Bunhia – copxki ta có:

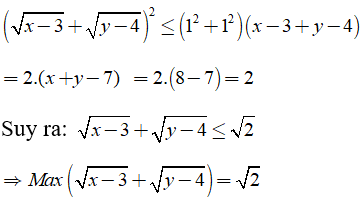
Chọn đáp án B.

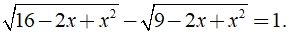
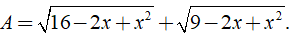
Câu 28: Cho Tính giá trị của biểu thức

A. A = 6        B. A = 3        C. A = 5        D. A = 7

Lời giải:

Ta có:

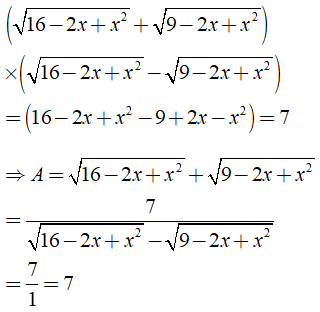
Chọn đáp án D.

Câu 29: Cho biểu thức A = (x³ + 12x - 31)²⁰¹². Tính giá trị của A tại

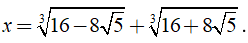
A. A = 2²⁰¹²        B. A = 1        C. A = 2¹⁰⁰⁶        D. 0

Lời giải:

Ta có:

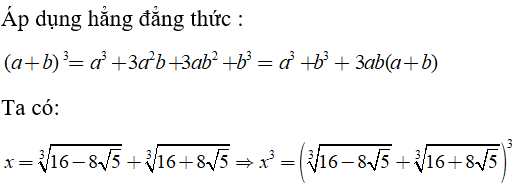
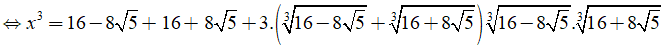
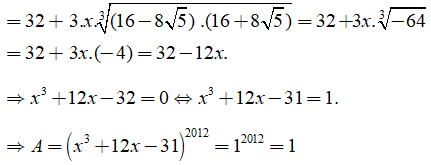
Chọn đáp án B.

Câu 30: Nghiệm của phương trình

là ?

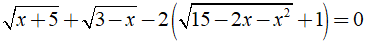
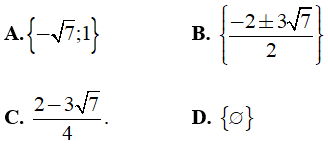
Lời giải:

Điều kiện x ∈ [-5; 3]

Ta có:

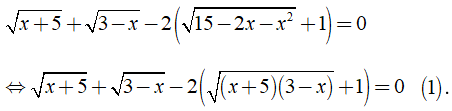
Đặt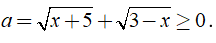

Khi đó

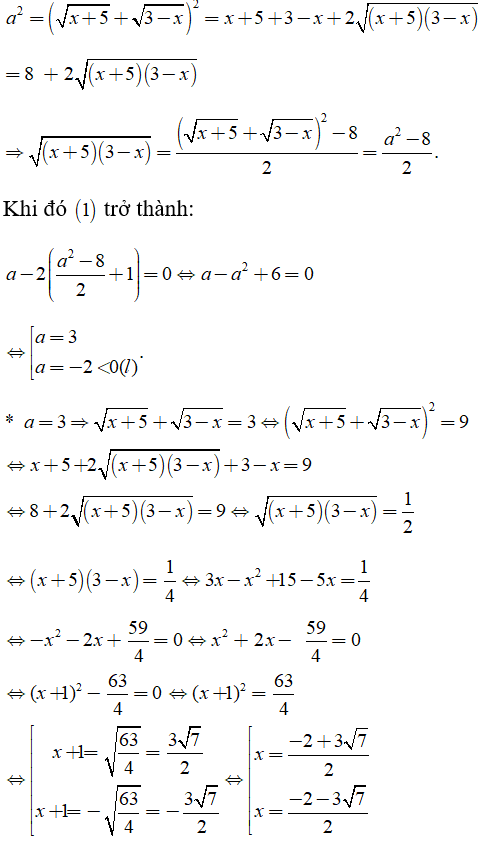
Chọn đáp án B.

Câu 31: Cho biểu thức

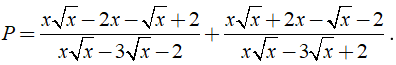
Với giá trị nào của x thì A > 1

Lời giải:

Điều kiện x ≥ 0; x ≠ 1; x ≠4.

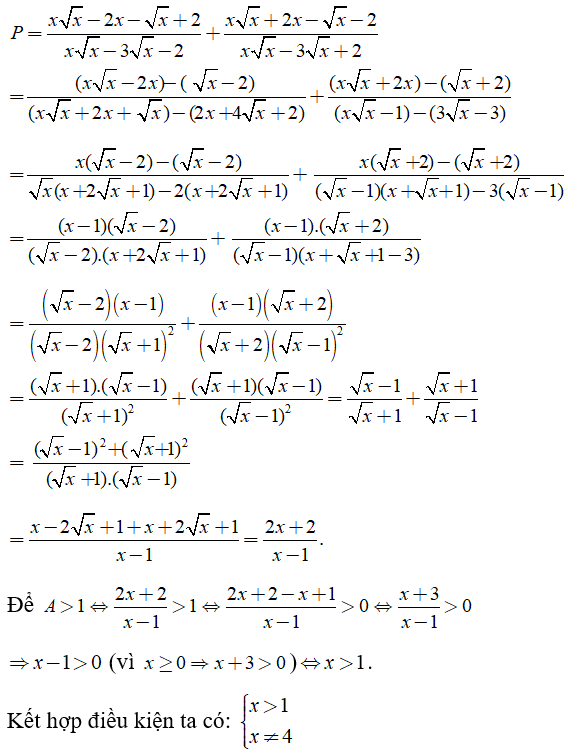
Chọn đáp án C.

Câu 32: Giá trị x, y, z để thỏa mãn

là ?

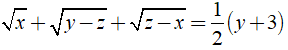
A. x = 1; y = 3; z = 2        B. x = 1; y = 2; z = 4

C. x = 4; y = 3; z = 2        D. x = 1; y = 2; z = 2

Lời giải:

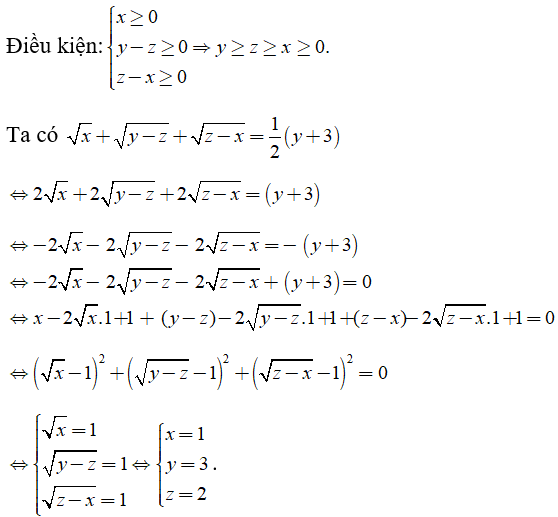
Chọn đáp án A.

Câu 33: Cho các biểu thức 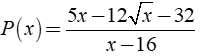và Q(x) = x + √x + 3. Tìm số nguyên x₀ sao cho P(x₀) và Q(x₀) là các số nguyên, đồng thời P(x₀) là ước của Q(x₀).

A. x₀ = 4        B. x₀ = 1        C. x₀ = 3        D. x₀ = 2

Lời giải:

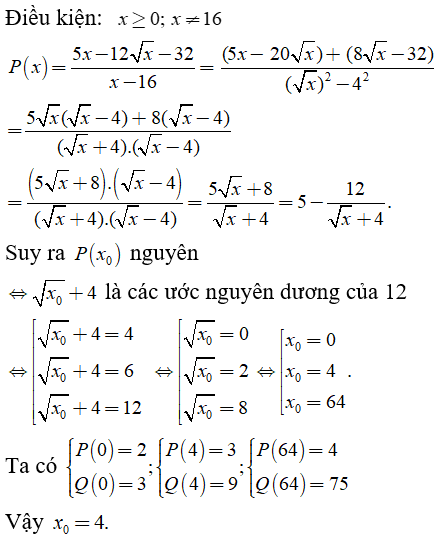
Chọn đáp án A.

Câu 34: Cho biểu thức

P =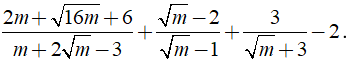

Tìm giá trị tự nhiên m để P là số tự nhiên ?

A. m = 9        B. m = 4        C. m ∈ {4; 9}        D. m = 1

Lời giải:

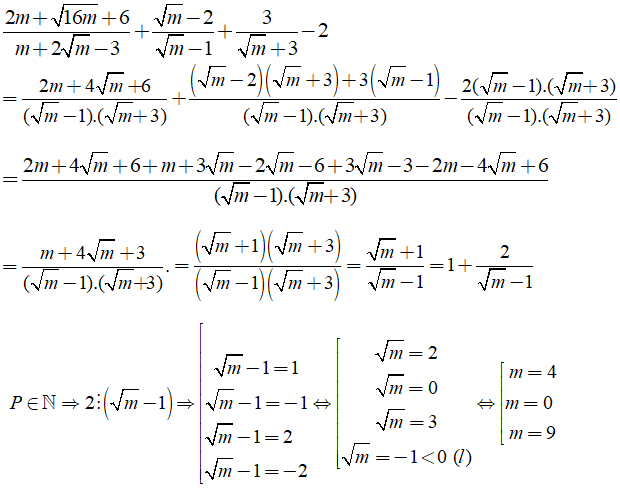
Thử lại, với m= 4 thì P =3 ( thỏa mãn)

Với m = 0 thì P = -1 ( không là số tự nhiên).

Với m = 9 thì P = 2 ( thỏa mãn)

Vậy m = 4 hoặc m = 9.

Chọn đáp án C.

Câu 35: Cho x, y, z > 0 thỏa mãn xy + yz + zx = 1. Tính giá trị của biểu thức:

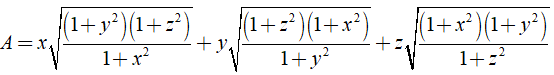
A. A = 1        B. A = 3        C. A = 2        D. A = 0

Lời giải:

Vì x, y ,z > 0 nên x + y > 0; y + z > 0 và x + z > 0

Ta có:

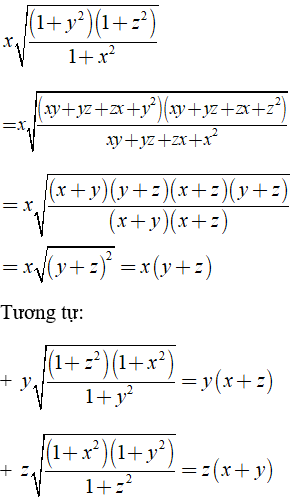
Khi đó

A = x(y + z) + y(x + z) + z(x + y)

= xy + xz + xy + yz + xz + zy = 2(xy + yz + zx) = 2

Chọn đáp án C.