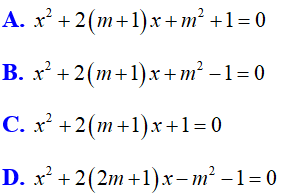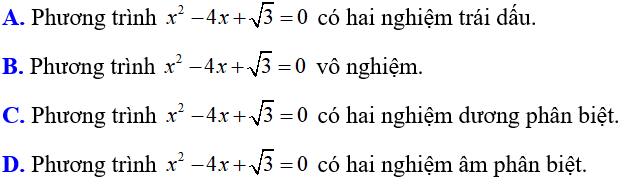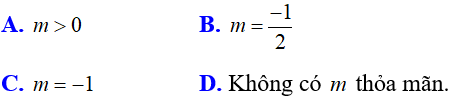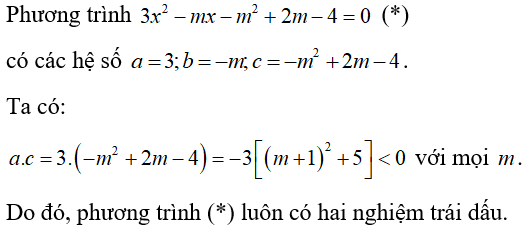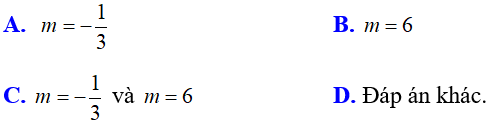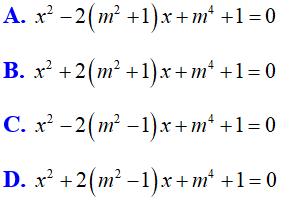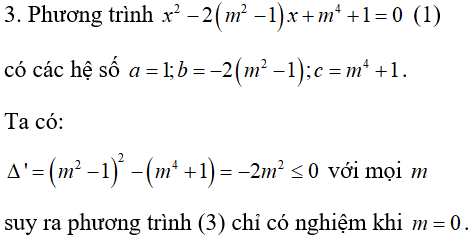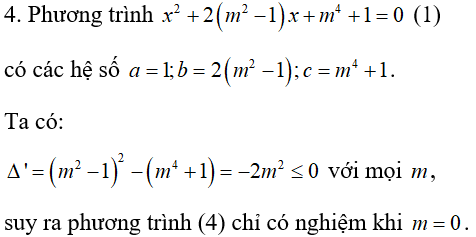Cách xét dấu các nghiệm của phương trình bậc hai cực hay, có đáp án | Toán lớp 9

Cách xét dấu các nghiệm của phương trình bậc hai cực hay, có đáp án

Với Cách xét dấu các nghiệm của phương trình bậc hai cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xét dấu các nghiệm của phương trình bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Cho phương trình ax² + bx + c = 0 (a ≠ 0)

Bước 1: Xác định hệ số a; b; c.

Bước 2: Tính Δ = b² - 4ac (hoặc Δ' = b'² - ac) để kiểm tra phương trình có nghiệm hay không.

Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ' ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình: .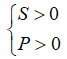

+) Phương trình có hai nghiệm cùng dấu: P > 0.

+) Phương trình có hai nghiệm dương: .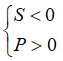

+) Phương trình có hai nghiệm âm: .

+) Phương trình có hai nghiệm trái dấu: P < 0.

Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0. hoặc a.c < 0.

Bước 4: Kết luận.

B. Các ví dụ điển hình

Ví dụ 1: Cho phương trình x² - 2x + 1 - m² = 0 với m là tham số. Khẳng định nào sau đây là đúng?

Lời giải

Chọn D

Ví dụ 2: Giá trị nguyên nhỏ nhất của tham số m để phương trình x² - 2(m + 7)x + m² - 4 = 0 có hai nghiệm trái dấu là:

Lời giải

Chọn C

Ví dụ 3: Phương trình 2x² + (2m - 1)x + m - 1 = 0 có hai nghiệm bằng nhau về giá trị tuyệt đối nhưng trái dấu nhau khi:

Lời giải

Chọn C

C. Bài tập vận dụng

Bài 1: Cho phương trình bậc hai (m - 1)x² - 2mx + m + 2 = 0 (với m là tham số). Chọn khẳng định sai trong các khẳng định sau:

Lời giải:

Đáp án A

Bài 2: Phương trình nào sau đây luôn có hai nghiệm trái dấu với mọi tham số m?

Lời giải:

Đáp án D

Bài 3: Chọn khẳng định đúng trong các khẳng định sau:

Lời giải:

Đáp án C

Bài 4: Cho các phương trình:

Số phương trình có hai nghiệm âm phân biệt là:

Lời giải:

Đáp án B

Bài 5: Giá trị của m để phương trình 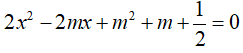có nghiệm âm là:

Lời giải:

Đáp án C

Bài 6: Biết rằng phương trình 3x² - mx - m² + 2m - 4 = 0 luôn có nghiệm với mọi tham số m. Chọn khẳng định đúng.

Lời giải:

Đáp án D

Bài 7: Tìm m để phương trình x² - (3m - 1)x + 10m = 0 có hai nghiệm x₁, x₂ là độ dài hai cạnh của tam giác vuông có cạnh huyền là 13.

Lời giải:

Đáp án B

Bài 8: Cho phương trình x² + (3m - 1)x + m² = 0 (với m là tham số). Giá trị nguyên nhỏ nhất của m để phương trình có hai nghiệm âm phân biệt là:

Lời giải:

Đáp án A

Bài 9: Tìm m để phương trình x² + 3mx + 2m² + 6 = 0 (m là tham số) có hai nghiệm là độ dài hai cạnh của hình chữ nhật có diện tích bằng 104.

Lời giải:

Đáp án A

Bài 10: Phương trình nào sau đây luôn có hai nghiệm âm với mọi tham số m?

Lời giải:

Đáp án B