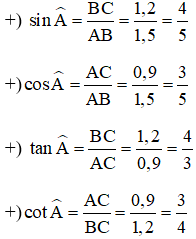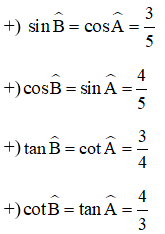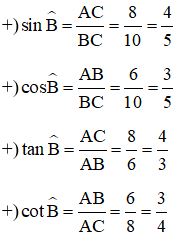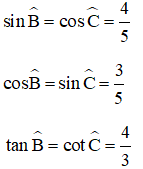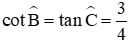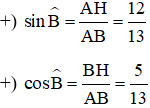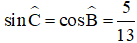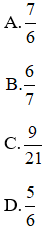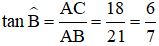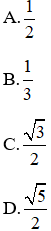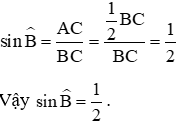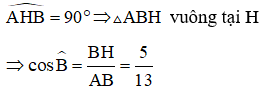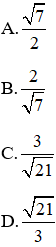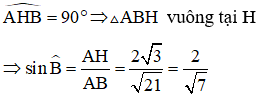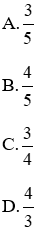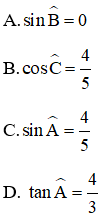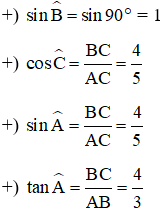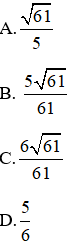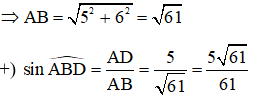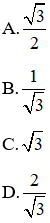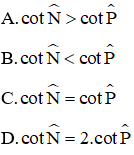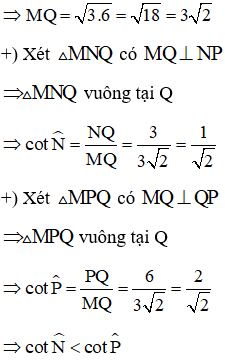Công thức, cách tính tỉ số lượng giác của góc nhọn cực hay | Toán lớp 9

Công thức, cách tính tỉ số lượng giác của góc nhọn cực hay

Với Công thức, cách tính tỉ số lượng giác của góc nhọn cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Công thức, cách tính tỉ số lượng giác của góc nhọn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

I/ Công thức tính tỉ số lượng giác của góc nhọn

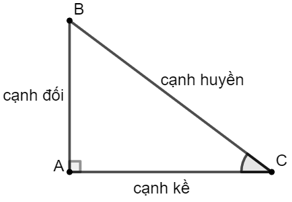
1. Cho góc nhọn α, từ một điểm bất kì trên một cạnh của góc α, kẻ đường vuông góc với cạnh kia.

Khi đó:

2. Nếu hai góc phụ nhau (có tổng số đo bằng 90⁰) thì: sin góc này bằng cos góc kia, tan góc này bằng cot góc kia

• Xác định cạnh đối, cạnh kề, cạnh huyền, viết tỉ số lượng giác theo định nghĩa

• Tính cạnh còn lại nhờ hệ thức Py – ta – go hoặc hệ thức về cạnh, đường cao

• Tính tỉ số lượng giác còn lại theo định lí tỉ số lượng giác hai góc phụ nhau

B. Ví dụ minh họa

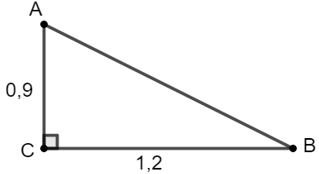
Ví dụ 1: Cho tam giác ABC vuông tại C, có BC = 1,2 cm, CA = 0,9 cm. Tính các tỉ số lượng giác của góc A, từ đó suy ra các tỉ số lượng giác của góc B.

Hướng dẫn giải:

Áp dụng định lí Py – ta – go cho tam giác ABC vuông tại C ta có:

⇔ AB² = AC² = BC²

⇒ AB² = 0,9² + 1,2² = 0,81 + 1,44 = 2,25

AB = 1,5 (cm)

Ta có:

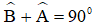
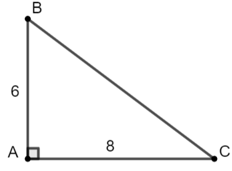
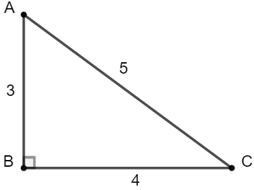
Do (tổng hai góc nhọn trong tam giác vuông) nên suy ra:

Ví dụ 2: Cho tam giác ABC vuông tại A, có AB = 6, AC = 8. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.

Hướng dẫn giải:

Áp dụng định lý Py – ta – go cho tam giác vuông ABC có:

BC² = AB² + AC²

⇔ BC² = 6² + 8²

⇔ BC² = 36 + 64 = 100

⇒ BC = 10

Ta có:

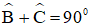
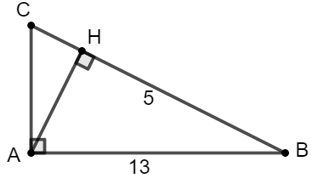
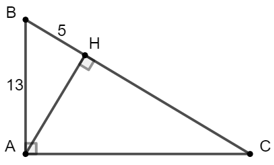
Do (tổng hai góc nhọn trong tam giác vuông) nên suy ra:

Ví dụ 3: Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính 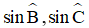biết rằng AB = 13, BH = 5

Hướng dẫn giải:

Xét tam giác ABH vuông tại H nên:

AH² = AB² - BH² (Định lý Py – ta – go)

⇔ AH² = 13² - 5² = 169 – 25 = 144 ⇒ AH = 12

Xét tam giác vuông ABH có:

Xét tam giác ABC vuông tại A có 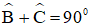(tổng hai góc nhọn trong tam giác vuông) nên suy ra:

Vậy .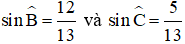

C. Bài tập trắc nghiệm

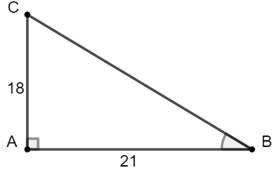
Bài 1: Cho tam giác ABC vuông tại A có AB = 21 cm, AC = 18 cm. Tính .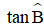

Hướng dẫn giải:

Xét tam giác ABC vuông tại A ta có:

Đáp án B.

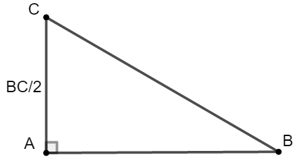
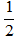
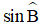
Bài 2: Tam giác ABC vuông tại A có AC = BC. Tính .

Hướng dẫn giải:

Xét ΔABC vuông tại A nên:

Đáp án A.

Bài 3: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Tính 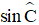của tam giác ABC biết rằng AB = 13; BH = 5.

Hướng dẫn giải:

Xét tam giác ABH có:

Xét tam giác ABC vuông tại A có 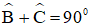(tổng hai góc nhọn trong tam giác vuông) nên suy ra:

Đáp án C.

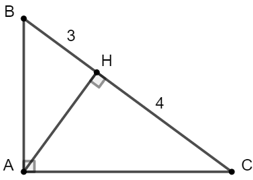
Bài 4: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Tính 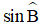của tam giác ABC biết rằng BH = 3; CH = 4.

Hướng dẫn giải:

Xét ΔABC vuông tại A có AH ⊥ BC tại H

+) AH² = BH.CH (Hệ thức lượng trong tam giác vuông)

⇔ AH² = 3.4 = 12 ⇒ AH =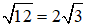

+) BC = BH + HC = 3 + 4 = 7

+) AB² = BH.BC (Hệ thức lượng trong tam giác vuông)

⇒ AB² = 3.7 = 21 ⇒ AB =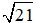

Xét tam giác ABH có:

Đáp án B.

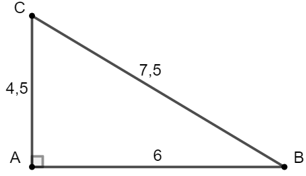
Bài 5: Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Tính 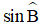của tam giác ABC.

Hướng dẫn giải:

Xét tam giác ABC có:

AB² + AC² = 6² + 4,5² = 56,25

BC = 7,5² = 56,25

⇒ AB² + AC² = BC²

Theo định lí Py – ta – go đảo suy ra tam giác ABC vuông tại A

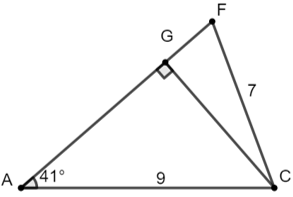
Bài 6: Cho tam giác ACF có = 41⁰, AC = 9, CF = 7. Tính ?

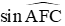
Hướng dẫn giải:

Bài 7: Cho tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 4 cm. Khẳng định nào sau đây là sai?

Hướng dẫn giải:

Xét ΔABC có:

AB² + BC² = 3² + 4² = 25

AC² = 5² = 25

⇒ AC² = AB² + BC² ⇒ ΔABC là tam giác vuông tại B.

Đáp án A.

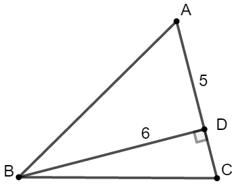
Bài 8: Cho ΔABC là tam giác nhọn có đường cao BD = 6. Biết AD = 5. Tính .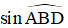

Hướng dẫn giải:

Xét ΔABD vuông tại D có:

AB² = AD² + BD² (Định lý Py – ta – go)

Đáp án B.

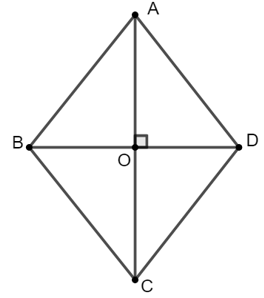
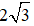
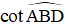
Bài 9: Cho hình thoi ABCD có độ dài hai đường chéo AC và BD lần lượt là 2, . Tính .

Hướng dẫn giải:

Ta có:

Đáp án B.

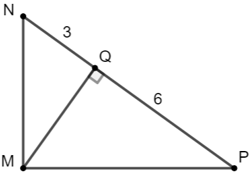
Bài 10: Đường cao MQ của ΔMNP vuông tại M chia cạnh huyền NP thành hai đoạn NQ = 3; PQ = 6. Khẳng định nào dưới đây là đúng?

Hướng dẫn giải:

+) Xét ΔMNP vuông tại M có MQ ⊥ NP (gt)

⇒ MQ² = NQ.PQ (hệ thức lượng trong tam giác vuông)

Đáp án B.