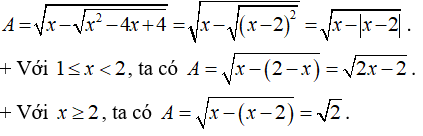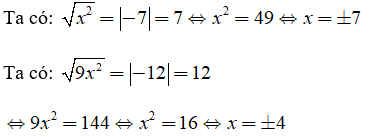Lý thuyết Căn thức bậc hai và hằng đẳng thức hay, chi tiết | Toán lớp 9
Lý thuyết Căn thức bậc hai và hằng đẳng thức hay, chi tiết
Tài liệu Lý thuyết Căn thức bậc hai và hằng đẳng thức hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Căn thức bậc hai và hằng đẳng thức từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.
A. Lý thuyết
I. CĂN THỨC BẬC HAI
1. Định nghĩa
Với A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.
2. Điều kiện có nghĩa(hay có nghĩa) của một căn thức bậc hai
√A xác định(có nghĩa) ⇔ A ≥ 0
3. Ví dụ cụ thể
- 
xác định ⇔ 3x ≥ 0 ⇔ x ≥ 0.
- 
xác định ⇔ 3 - 7x ≥ 0 ⇔ x ≤ 3/7.
- 
xác định ⇔ 2 - 3x ≥ 0 ⇔ x ≤ 2/3.
- 
xác định ⇔ x - 6 ≥ 0 ⇔ x ≥ 6.
- 
xác định.
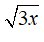
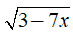
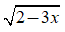
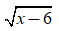
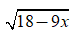
II. HẰNG ĐẲNG THỨC
Muốn khai căn một biểu thức, ta dùng hằng đẳng thức √(A2) = |A|.
Ví dụ 1: Rút gọn biểu thức
với a < 2
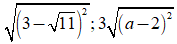
Giải:
Ví dụ 2: Tìm x biết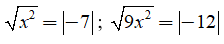 
Giải:
III. MỘT SỐ KIẾN THỨC CẦN NHỚ
1. Giá trị tuyệt đối
• Định nghĩa 
• Hệ quả
|A| ≥ 0, ∀ A
|A| = |-A|
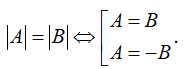
|A| = A ⇔ A ≥ 0; |A| = -A ⇔ A ≤ 0; |A| = 0 ⇔ A = 0
2. Dấu của một tích, một thương
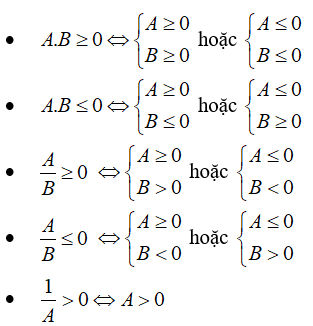
B. PHƯƠNG PHÁP GIẢI TOÁN
DẠNG 1: Tìm điều kiện để một để một căn thức bậc hai xác định.
• √A xác định (hay có nghĩa) ⇔ A ≥ 0
• Giải bất phương trình A ≥ 0
• Kết luận.
DẠNG 2: Khai căn một biểu thức – Tính giá trị một biểu thức chứa căn
• Khai căn nhờ hằng đẳng thức √(A2) = |A|
• Rút gọn
DẠNG 3: Phân tích thành nhân tử
• Viết A ≥ 0 thành (√A)2
• Sử dụng A2 - B2 = (A - B)(A + B)
• Sử dụng A2 ± 2AB + B2 = (A ± B)2
• Thêm, bớt tạo thành hằng đẳng thức
DẠNG 4: Giải phương trình
• Khai căn một biểu thức
• Giải phương trình chứa dấu giá trị tuyệt đối
B. Bài tập tự luận
Câu 1: Rút gọn các biểu thức sau:
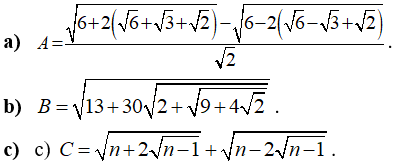
Lời giải:
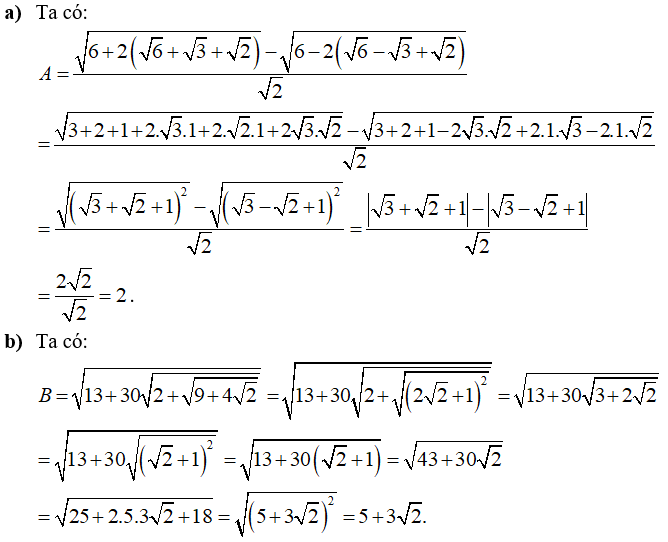
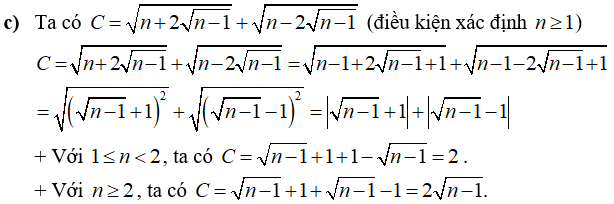
Câu 2: Giải các phương trình sau
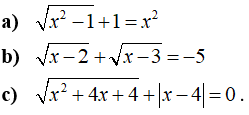
Lời giải:
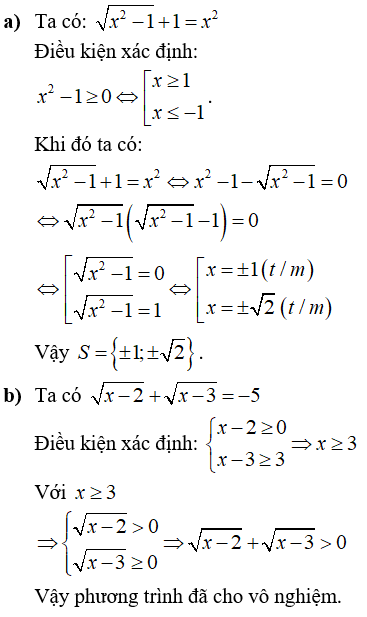
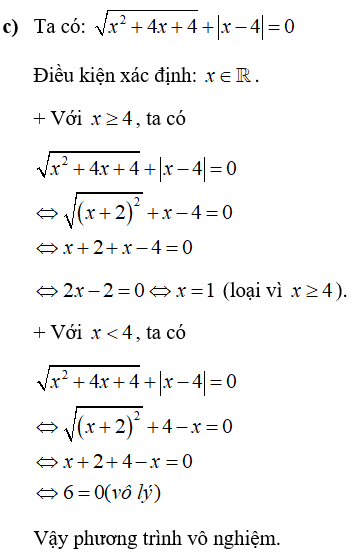
Câu 3: Cho biểu thức:
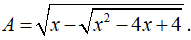
a) Tìm tập xác định của biểu thức.
b) Rút gọn biểu thức A.
Lời giải:
a) Điều kiện xác định:
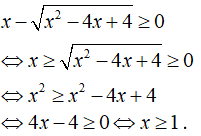
Vậy tập xác định là D = [1; +∞].
b) Ta có: .
