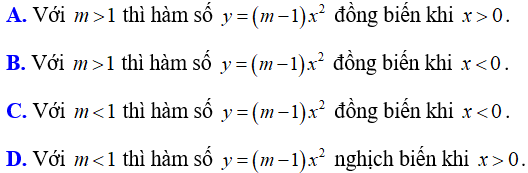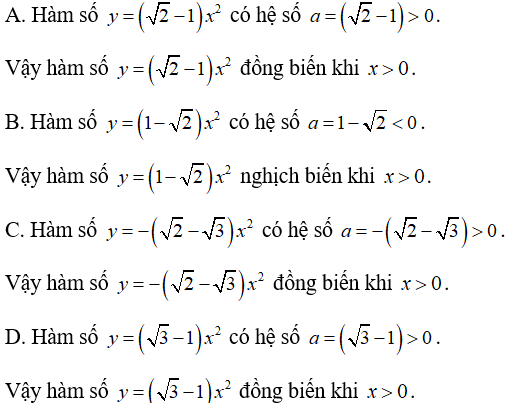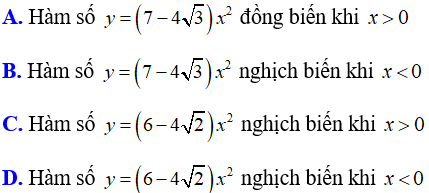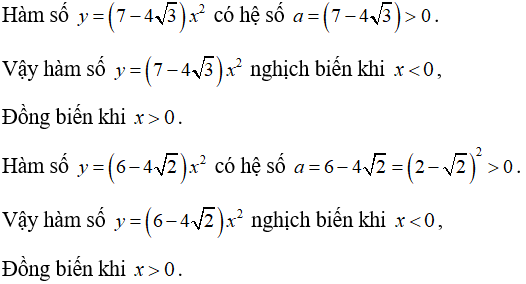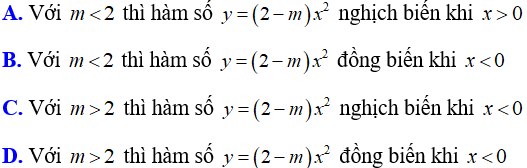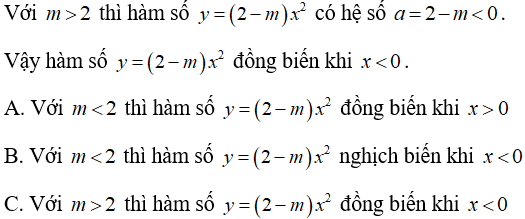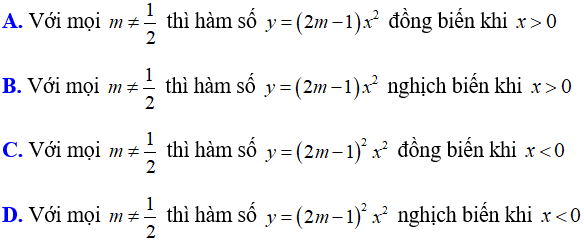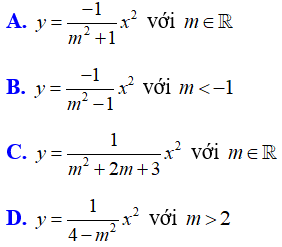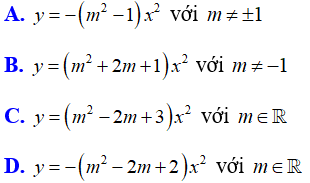Xét tính đồng biến, nghịch biến của hàm số cực hay, có đáp án | Toán lớp 9
Xét tính đồng biến, nghịch biến của hàm số cực hay, có đáp án
Với Xét tính đồng biến, nghịch biến của hàm số cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Xét tính đồng biến, nghịch biến của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
A. Phương pháp giải
Cho hàm số y = ax2 (a ≠ 0).
Bước 1: Xét dấu của hệ số a.
- Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
- Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Bước 2: Kết luận.
B. Các ví dụ điển hình
Ví dụ 1:Hàm số nào sau đây đồng biến khi x > 0?
Lời giải
Chọn A
Hàm số y = 2x2 có hệ số a = 2 > 0. Vậy hàm số y = 2x2 đồng biến khi x > 0.
Ví dụ 2: Cho hàm số y = (m - 1)x2 với m là tham số, m ≠ 1. Khẳng định nào sau đây sai?
Lời giải
Chọn B
Với m > 1 thì hàm số y = (m - 1)x2 có hệ số a = m - 1 > 0. Vậy hàm số y = (m - 1)x2 nghịch biến khi x < 0.
Ví dụ 3: Hàm số nào sau đây nghịch biến khi x < 0?
Lời giải
Chọn A
Hàm số y = m2x2 có hệ số a = m2 > 0 với mọi m < 0. Vậy hàm số y = m2x2 nghịch biến khi x < 0.
C. Bài tập vận dụng
Bài 1: Hàm số nào sau đây đồng biến khi x < 0?
Lời giải:
Đáp án C
Bài 2: Hàm số nào sau đây nghịch biến khi x < 0?
Lời giải:
Đáp án D
Bài 3: Hàm số nào sau đây nghịch biến khi x > 0?
Lời giải:
Đáp án B
Bài 4: Chọn khẳng định sai trong các khẳng định sau:
Lời giải:
Đáp án C
Bài 5: Cho hàm số y = (2 - m)x2 với m là tham số, m ≠ 2. Khẳng định nào sau đây đúng?
Lời giải:
Đáp án D
Bài 6: Cho hàm số y = (2m - 1)x2 với m là tham số,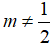 
. Chọn khẳng định đúng trong các khẳng định sau:
Lời giải:
Đáp án D
Bài 7: Với giá trị nào của m thì hàm số y = (3 + 2m)2 (với m là tham số, m ≠ -1,5) đồng biến khi x < 0?
Lời giải:
Đáp án
Bài 8: Tập hợp tất cả các giá trị của tham số m để hàm số y = (m2 + 4)x2 nghịch biến khi x > 0 là:
Lời giải:
Đáp án A
Bài 9: Hàm số nào sau đây đồng biến khi x > 0?
Lời giải:
Đáp án C
Bài 10: Hàm số nào sau đây luôn đồng biến khi x < 0?
Lời giải:
Đáp án D
