Lý thuyết Phương trình bậc nhất hai ẩn hay, chi tiết | Toán lớp 9

Lý thuyết Phương trình bậc nhất hai ẩn hay, chi tiết

Tài liệu Lý thuyết Phương trình bậc nhất hai ẩn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Phương trình bậc nhất hai ẩn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

I. ĐỊNH NGHĨA

Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng: ax + by = c, trong đó a, b, c là các số đã biết (trong đó a ≠ 0 hoặc b ≠ 0 ).

* Trong phương trình ax + by = c, nếu giá trị của vế trái tại x = x₀ và y =y₀ bằng vế phải thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình.

Chú ý: Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x₀; y₀) được biểu diễn bởi điểm có tọa độ (x₀; y₀).

Ví dụ: Các phương trình bậc nhất hai ẩn là 2x + y = 1; x - y = 2; ....

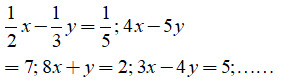
II. TẬP NGHIỆM CỦA PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c kí hiệu là (d).

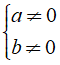
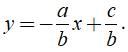
Nếu thì (d) là đồ thị của hàm số bậc nhất

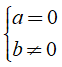
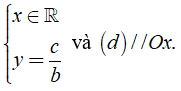
Nếu thì công thức nghiệm là

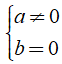
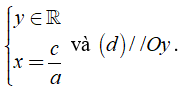
Nếu thì công thức nghiệm là

III. VÍ DỤ CỤ THỂ

Câu 1: Tìm hai nghiệm của phương trình x + y = 2 (1)

Hướng dẫn:

    + Cho y = 0 ⇒ x = 2 → (2; 0) là một nghiệm của phương trình (1).

    + Cho y = 1 ⇒ x = 1 → (1; 1) là một nghiệm của phương trình (1).

⇒ (2; 0); (1; 1) là hai nghiệm cần tìm của phương trình x + y = 2.

Câu 2: Cho hai cặp số (1; 2) và (0; 1). Hỏi cặp nào là nghiệm của phương trình 2x + 3y = 8 ?

Hướng dẫn:

    + Ta có 2.1 + 3.2 = 8 ⇒ (1; 2) là cặp nghiệm của phương trình 2x + 3y = 8.

    + Ta có 2.0 + 3.1 = 3 ≠ 8 ⇒ (0; 1) không phải là cặp nghiệm của phương trình 2x + 3y = 8

Câu 3: Cặp số (1:1) có phải là nghiệm của phương trình x + y = 1 không?

Hướng dẫn:

Ta có: 1 + 1 = 2 ≠ 1 nên (1;1) không là nghiệm của phương trình x + y = 1

B. Bài tập tự luận

Câu 1: Cho phương trình (m - 2)x + (m - 1)y = 1 (m là tham số). Chứng minh rằng đường thẳng biểu diễn tập nghiệm của phương trình này luôn đi qua một điểm cố định với mọi giá trị của m

Lời giải:

Gọi (d) là đường thẳng biểu diễn tập nghiệm của phương trình

Vậy (d) luôn đi qua một điểm cố định là M(-1; 1)

Câu 2: Tìm các điểm nằm trên đường thẳng 8x + 9y = -79 , có hoành độ và tung độ là các số nguyên và nằm trong góc vuông phần tư thứ III

Lời giải:

Ta cần tìm nghiệm nguyên của phương trình 8x + 9y = -79 , rút x từ phương trình ta được:

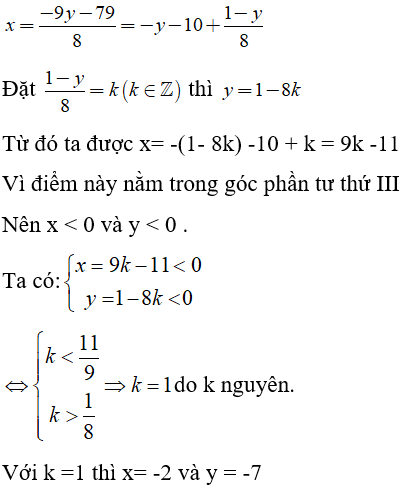
Vậy có 1 điểm duy nhất phải tìm là (-2; -7)