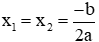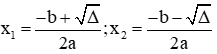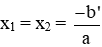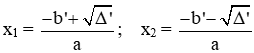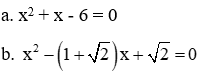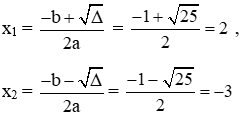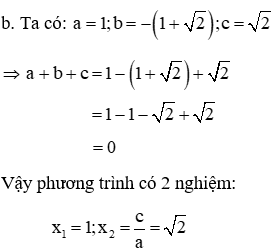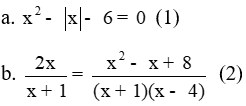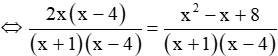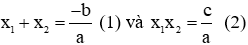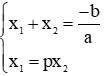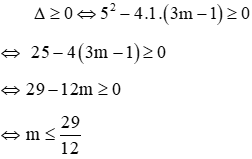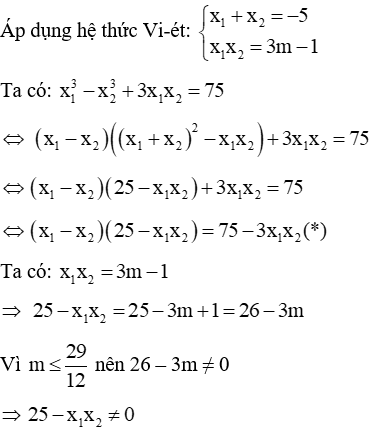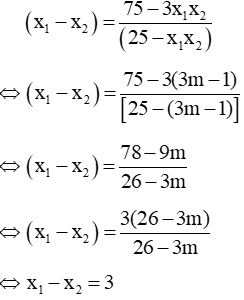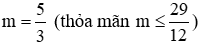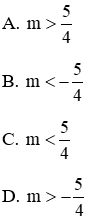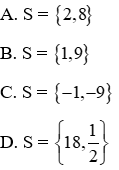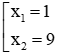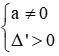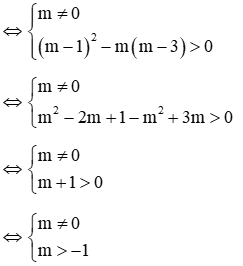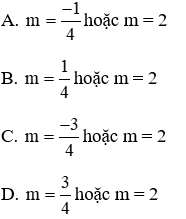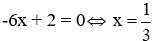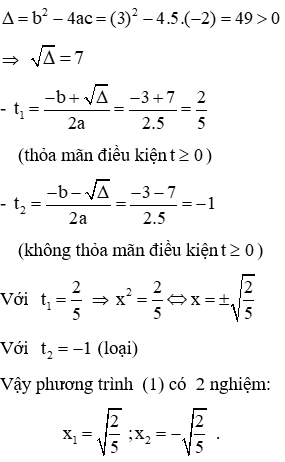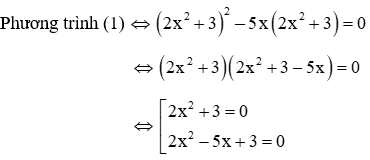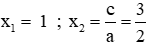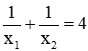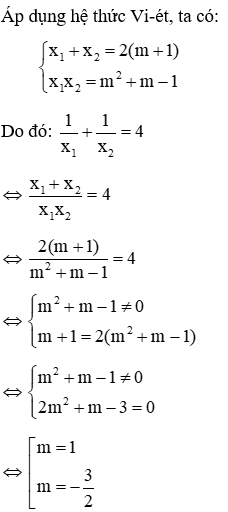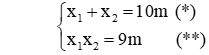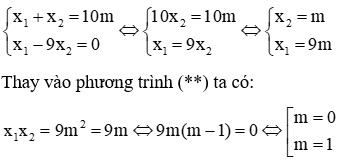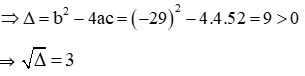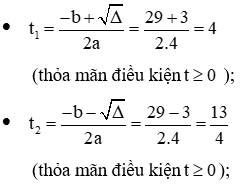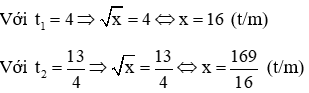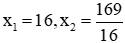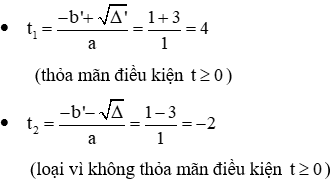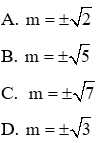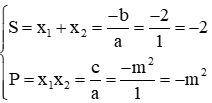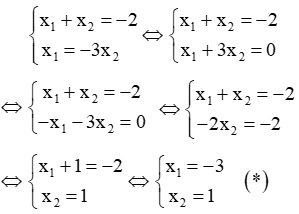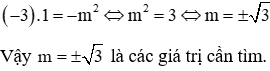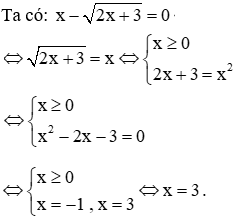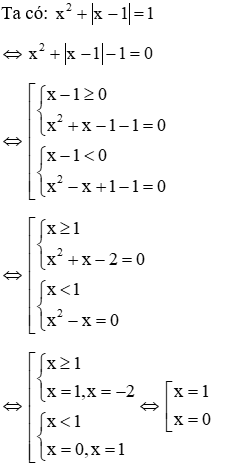Cách giải các dạng toán giải phương trình bậc hai một ẩn cực hay | Toán lớp 9

Cách giải các dạng toán giải phương trình bậc hai một ẩn cực hay

Với Cách giải các dạng toán giải phương trình bậc hai một ẩn cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập các dạng toán giải phương trình bậc hai một ẩn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Dạng 1: Giải phương trình bậc hai ax² + bx + c = 0 (a ≠ 0)

1. Phương pháp.

- Xác định các hệ số a, b, c của phương trình bậc hai.

- Nếu a + b + c = 0 thì phương trình có 2 nghiệm: x₁ = 1, 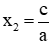(1)

- Nếu a – b + c = 0 thì phương trình có 2 nghiệm: x₁ = 1, 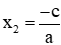(2)

- Nếu không rơi vào trường hợp (1) và (2) thì tính ∆ = b² – 4ac

+ ∆ < 0 thì phương trình vô nghiệm

+ ∆ = 0 thì phương trình có nghiệm kép:

+ ∆ < 0 thì phương trình có 2 nghiệm phân biệt

Lưu ý: Nếu b = 2bꞌ thì giải phương trình theo công thức nghiệm thu gọn

Ta có ∆ꞌ = (bꞌ)² – ac

+ Nếu ∆ꞌ < 0 thì phương trình vô nghiệm

+ Nếu ∆ꞌ = 0 thì phương trình có nghiệm kép:

+ Nếu ∆ꞌ > 0 thì phương trình có 2 nghiệm phân biệt

2. Ví dụ

Giải các phương trình sau

Giải

a. Ta có: a = 1; b = 1; c = - 6 ⇒ ∆ = b² – 4ac = 1 + 24 = 25 > 0

Vậy phương trình có hai nghiệm phân biệt:

Dạng 2: Tìm 2 số khi biết tổng và tích của hai số đó

1. Phương pháp:

Nếu hai số x₁; x₂ có x₁ + x₂ = S ; x₁.x₂ = P thì x₁ và x₂ có thể là hai nghiệm của phương trình bậc hai: x² - Sx + P = 0

Tính ∆ = (-S)² – 4P = S² – 4P = ?

+ Nếu S² – 4P < 0 thì không tồn tại x₁ và x₂.

+ Nếu S² – 4P ³ 0 thì tồn tại hai nghiệm x₁ và x₂ tính theo công thức nghiệm

Hoặc tính Tính ∆ꞌ = (-Sꞌ)² – P = (Sꞌ)² – P = ? ( với S = 2Sꞌ)

+ Nếu (Sꞌ)² – P < 0 thì không tồn tại x₁ và x₂.

+ Nếu (Sꞌ)² – 4P ³ 0 thì tồn tại hai nghiệm x₁ và x₂ tính theo công thức nghiệm thu gọn

2. Ví dụ

Tìm hai số u và v biết: u + v = 42 và u.v = 441

Giải

Ta có: u + v = 42 và u.v = 441 nên u và v có thể là nghiệm của phương trình bậc hai:

x² – 42x + 441 = 0 (*)

Ta có: ∆ꞌ = (- 21)² - 441 = 0

Phương trình (*) có nghiệm x₁ = x₂ = 21

Vậy u = v = 21

Dạng 3: Phương trình quy về phương trình bậc hai

1. Phương pháp.

- Xác định điều kiện của phương trình nếu có

- Quy đồng, biến đổi, đặt ẩn phụ...để đưa phương trình đã cho về phương trình bậc hai.

2. Ví dụ

Giải phương trình sau

Giải

a. Đặt t = |x| (t ≥ 0) ⇒ t² = x². Khi đó phương trình (1) trở thành: t² – t – 6 =0

Ta có: ∆ = b² – 4ac = (-1)² – 4.1 .(-6) = 25 > 0

Do đó phương trình (1) có 2 nghiệm phân biệt

(thỏa mãn t ≥ 0)

(không thỏa mãn t ≥ 0)

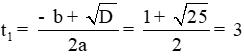
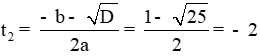
Với t = 3 ⇔ |x| = 3 ⇔ x = 3 hoặc x = -3

Vậy phương trình có 2 nghiệm: x = 3 hoặc x = -3

b. ĐK: x ≠ -1; x ≠ 4

Phương trình (2)

⇒ 2x(x- 4) = x² – x + 8

⇔ x² – 7x – 8 = 0 (*)

Do a – b + c = 1- (-7) + (- 8) = 0 nên phương trình (*) có hai nghiệm

x₁ = -1(không thoả mãn ĐK) ; x₂ = 8 (thoả mãn ĐK)

Vậy phương trình (2) có nghiệm x = 8

Dạng 4: Phương trình bậc hai chứa tham số

1.Phương pháp: cho phương trình ax² + bx + c =0(a ≠ 0)

a. Điều kiện để phương trình

1. Có nghiệm ⇔ Δ ≥ 0

2. Vô nghiệm ⇔ Δ < 0

3. Có nghiệm kép ⇔ Δ = 0

4. Có hai nghiệm phân biệt (khác nhau) ⇔ Δ > 0

5. Hai nghiệm cùng dấu ⇔ Δ ≥ 0 và P > 0

6. Hai nghiệm trái dấu khi a.c < 0

7. Hai nghiệm dương (lớn hơn 0) ⇔ Δ ≥ 0 ; S > 0 và P > 0

8. Hai nghiệm âm (nhỏ hơn 0) ⇔ Δ ≥ 0 ; S < 0 và P > 0

9. Hai nghiệm đối nhau ⇔ Δ ≥ 0 và S = 0

10. Hai nghiệm nghịch đảo của nhau ⇔ Δ ≥ 0 và P = 1

11. Hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn khi ac < 0 và S < 0

12. Hai nghiệm trái dấu và nghiệm dương có giá trị tuyệt đối lớn hơn khi

ac < 0 và S > 0

b. Điều kiện để phương trình có hai nghiệm phân biệt sao cho x₁ = px₂ (với p là một số thực)

B1- Tìm điều kiện để phương trình có hai nghiệm phân biệt .

B2- Áp dụng định lý Vi - ét tìm:

B3- Kết hợp (1) và (3) giải hệ phương trình:

⇒ x₁ và x₂

B4- Thay x₁ và x₂ vào (2) ⇒ Tìm giá trị tham số.

c. Điều kiện để phương trình có hai nghiệm thỏa mãn điều kiện: |x₁ - x₂|= k (k ∈ R)

- Bình phương trình hai vế: (x₁ - x₂)² = k² ⇔ ... ⇔ (x₁ + x₂)²-4x₁x₂ = k²

- Áp dụng định lý Vi-ét tính x₁ + x₂ và x₁x₂ thay vào biểu thức ⇒ kết luận.

d. So sánh nghiệm của phương trình bậc hai với một số bất kỳ:

B1: Tìm điều kiện để phương trình có nghiệm (∆ ≥ 0)

B2: Áp dụng Vi-ét tính x₁ + x₂ và x₁x₂ (*)

+/ Với bài toán: Tìm m để phương trình có hai nghiệm > α

Ta có 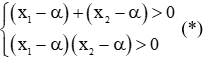. Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm < α

Ta có 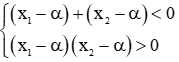(*). Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm: x₁ < α < x₂

Ta có (x₁ - α)(x₂ - α) < 0 (*) .Thay biểu thức Vi-ét vào (*) để tìm m

2. Ví dụ

Cho phương trình x² + 5x + 3m - 1 = 0 (x là ẩn số, m là tham số)

a. Tìm m để phương trình có hai nghiệm

b. Tìm m để phương trình có hai nghiệm thỏa mãn x₁³ - x₂³ + 3x₁x₂ = 75

Giải

a. Phương trình có 2 nghiệm khi:

Vậy với 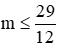thì phương trình có hai nghiệm

b. Với 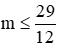thì phương trình có 2 nghiệm x₁, x₂

Chia hai vế của (*) cho 25 - x₁x₂ ≠ 0 ta được:

Kết hợp x₁ + x₂ = -5 suy ra x₁ = -1; x₂ = -4. Thay vào x₁x₂ = 3m - 1 suy ra

Vậy 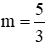là giá trị cần tìm.

B. Bài tập

Câu 1: Cho phương trình x² - (2m - 1)x + m² - 1 = 0 (x là ẩn số)

Tìm điều kiện của m để phương trình đã cho có hai nghiệm phân biệt.

Giải

Δ = (2m - 1)² - 4.(m² - 1) = 5 - 4m

Phương trình có hai nghiệm phân biệt khi Δ > 0 ⇔ 5 - 4m > 0 ⇔ m < 5/4

Đáp án là C

Câu 2: Tập nghiệm của phương trình x² - 10x + 9 = 0 là

Giải

Phương trình x² - 10x + 9 = 0 có a + b + c = 1 + (-10) + 9 = 0 nên phương trình có hai nghiệm phân biệt là

Vậy tập nghiệm của phương trình là: S = {1,9}

Đáp án B

Câu 3: Tìm m để phương trình mx² –2(m – 1)x + m - 3 = 0 (1) có 2 nghiệm phân biệt

A. m > -2 và m ≠ 0

B. m > -1 và m ≠ 0

C. m > 2 và m ≠ 1

D. m > 3 và m ≠ 0

Giải

Điều kiện để phương trình (1) có 2 nghiệm phân biệt là

Vậy với m > -1 và m ≠ 0 thì phương trình có hai nghiệm phân biệt

Đáp án là B

Câu 4: Tìm m để phương trình (m – 2)x² –2(m + 1)x + m = 0 (1) có 1 nghiệm

Giải

TH1: m-2 = 0 ⇔ m = 2, thay m = 2 vào phương trình (1) ta được:

-6x + 2 = 0

với m = 2 phương trình (1) có nghiệm duy nhất nên m = 2 nhận

TH2: m - 2 ≠ 0 ⇔ m ≠ 2, khi đó (1) là phương trình bậc hai.

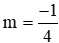
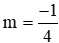
với phương trình (1) có nghiệm duy nhất nên nhận

Vậy với 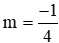hoặc m = 2 thì phương trình (1) có nghiệm duy nhất

Đáp án A

Câu 5: Cho phương trình x² –(m - 1)x - m = 0 (1), kết luận nào sau đây đúng về phương trình (1)

Phương trình vô nghiệm với mọi m

B. Phương trình có nghiệm kép với mọi m

C. Phương trình có 2 nghiệm phân biệt với mọi m

D. Phương trình có nghiệm với mọi m

Giải

Phương trình (1) là phương trình bậc hai có hệ số a = 1, b = -m + 1, c = -m

⇒ a – b + c = 1 + m – 1 – m = 0

Do đó (1) có 2 nghiệm x = -1, x = m

Vì nếu m = -1 thì (1) có 1 nghiệm x = -1 nên ta chỉ có thể khẳng định (1) có nghiệm với mọi m

Đáp án D

Câu 6: Số nghiệm của phương trình: 5x⁴ + 3x² – 2 = 0 (1)

A. 1

B. 2

C. 3

D. 4

Giải

Đặt t = x² (điều kiện: t ≥ 0), phương trình (1) có dạng: 5t² + 3t – 2 = 0

Ta có: a = 5, b = 3, c = -2

Đáp án B

Câu 7: Số nghiệm của phương trình (2x² + 3)² – 10x³ – 15x = 0 (1)

A. 1

B. 2

C. 3

D. 4

Giải

+) 2x² + 3 = 0 ⇔ 2x² = –3 ⇒ x² = 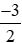(vô nghiệm)

+) 2x² – 5x + 3 = 0, đây là phương trình bậc hai có: a + b + c = 2 – 5 + 3 = 0

nên có 2 nghiệm:

Vậy phương trình đã cho có 2 nghiệm:

Đáp án B

Câu 8: Cho phương trình x² - 2(m + 1)x + m² + m - 1 = 0 (m là tham số)

Tìm m để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn điều kiện

A. m = 2

B. m = 3

C. m = 0

D. m = 1

Giải

Ta có: Δ' = (m + 1)² - m² - m + 1 = m² + 2m + 1 - m² - m + 1 = m+ 2

Phương trình đã cho có hai nghiệm phân biệt ⇔ Δ' > 0 ⇔ m + 2 > 0 ⇔ m > -2

Kết hợp với điều kiện m > -2 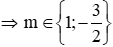là các giá trị cần tìm.

Đáp án D

Câu 9: Tìm m để phương trình x² – 10mx + 9m = 0 có hai nghiệm phân biệt thỏa mãn x₁ - 9x₂ = 0

A. m = 1

B. m = 2

C. m = 3

D. m = 4

Giải

Ta có: Δ' = (-5m)² - 1.9m = 25m² - 9m

Điều kiện phương trình đã cho có hai nghiệm phân biệt là: Δ' > 0 ⇔ 25m² - 9m > 0

Theo hệ thức Vi-ét ta có:

từ (*) và giả thiết ta có hệ phương trình:

Với m = 0 ta có Δ' = 25m² - 9m = 0 không thỏa mãn điều kiện phương trình có 2 nghiệm phân biệt.

Với m = 1 ta có Δ' = 25m² - 9m = 16 > 0 thỏa mãn điều kiện để phương trình có 2 nghiệm phân biệt.

Kết luận: Vậy với m = 1 thì phương trình đã cho có 2 nghiệm phân biệt x₁, x₂ thỏa mãn điều kiện x₁ - 9x₂ = 0.

Đáp án A

Câu 10: Tổng các nghiệm của phương trình x² – x + 5 = 0 là

A. -1

B. 1

C. Không tồn tại

D. 5

Giải

Phương trình x² – x + 5 = 0 có ∆ = (-1)² – 4.1.5 = 1 – 20 = -19 < 0

phương trình vô nghiệm nên không tồn tại tổng các nghiệm

Đáp án là C

Câu 11: Số nghiệm của phương trình 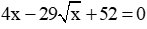là

A. 1

B. 2

C. 3

D. 4

Giải

Điều kiện: x ≥ 0

Đặt √x = t (điều kiện: x ≥ 0), khi đó phương trình đã cho trở thành: 4t² - 29t + 52 = 0 (1)

có a = 4, b = -29, c = 52

Phương trình (1) có hai nghiệm phân biệt:

KL: Vậy phương trình đã cho có 2 nghiệm là:

Đáp án B

Câu 12: Tổng các nghiệm của phương trình 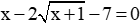là

A. 13

B. 14

C. 15

D. 16

Giải

Phương trình (1) có hai nghiệm phân biệt:

Với t = 4 ⇒ √(x+1) = 4 ⇔ x + 1 = 16 ⇔ x = 15 (t/m)

Vậy phương trình đã cho có nghiệm x = 15, do đó tổng các nghiệm bằng 15

Đáp án C

Câu 13: Cho phương trình x² + 2x - m² - 1 = 0 (m là tham số). Khẳng định nào sau đây đúng

A. Phương trình luôn có hai nghiệm phân biệt với mọi m.

B. Phương trình vô nghiệm

C. Phương trình có nghiệm kép khi m = 2

D. Phương trình có một nghiệm x = -3 khi m = 1

Giải

Ta có: Δ' = 1² - 1.(-m² - 1) = 1 + m² + 1 = m² + 2 > 0, với mọi m

Vì Δ' > 0 với mọi m nên phương trình luôn có hai nghiệm phân biệt với mọi m.

Đáp án A

Câu 14: Cho phương trình x² + 2x - m² = 0

Tìm m để phương trình trên có hai nghiệm thỏa: x₁ = -3x₂

Giải

Ta có: Δ' = 1² - 1.(-m²) = 1 + m² = m² + 1 > 0, với mọi m

Vì Δ' > 0 với mọi m nên phương trình luôn có hai nghiệm phân biệt x₁, x₂ với mọi m.

theo Vi-ét ta có:

Ta có x₁ + x₂ = -2 (do trên) và x₁ = -3x₂ nên ta có hệ phương trình sau:

Thay (*) vào biểu thức x₁x₂ = -m² ta được:

Đáp án D

Câu 15: Cho phương trình 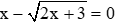. Chọn khẳng định sai

A. Phương trình có nghiệm dương

B. Phương trình có một nghiệm

C. Phương trình có nghiệm là số chia hết cho 3

D. Phương trình có nghiệm âm

Giải

Vậy phương trình đã cho có nghiệm là x = 3

Đáp án D

Câu 16: Số nghiệm của phương trình x² + |x - 1| = 1 là

A. 1

B. 2

C. 3

D. 4

Giải

Vậy phương trình có hai nghiệm

Đáp án B