Bài tập Hệ thức về góc và cạnh trong tam giác vuông chọn lọc, có lời giải | Toán lớp 9

Bài tập Hệ thức về góc và cạnh trong tam giác vuông chọn lọc, có lời giải

Với Bài tập Hệ thức về góc và cạnh trong tam giác vuông chọn lọc, có lời giải Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ thức về góc và cạnh trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Bài 1: Giải tam giác ABC vuông tại A, biết AB = 3,8 cm ; góc B bằng 51⁰

Bài 2: Giải tam giác ABC vuông tại A, biết AB = 2,7 cm; AC = 3,5 cm

Bài 3: Giải tam giác ABC, biết AB = 4 cm; góc B bằng 60⁰, góc C bằng 45⁰

Bài 4: Cho tam giác ABC nhọn, BC = a; CA = b; AB = c. Chứng minh rằng:

    a = b.cos⁡C + c.cosB

Bài 5: Cho đoạn thẳng AB có trung điểm O. Vẽ về một phía của AB các tia Ax, By vuông góc với AB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho góc COD bằng 90⁰. Chứng minh rằng AB² = 4AC.BD

Bài 6: Cho tam giác ABC vuông tại A, đường cao AD (D ∈ BC). Gọi E, F theo thứ tự là trung điểm của D trên AB, AC. Chứng minh rằng

    DB.DC = EA.EB + FA.FC

Đáp án và hướng dẫn giải

Bài 1:

    góc C bằng 39⁰; AC = 4,7 cm; BC = 6 cm

Bài 2:

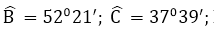
    BC = 4,4 cm

Bài 3:

    Vẽ đường cao AH

    AH = 2√3 cm; BH = 2cm; CH = 2√3 cm

    BC = BH + CH = 2 + 2√3 (cm)

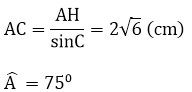
Bài 4:

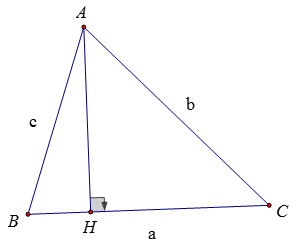
    Vẽ đường cao AH, điểm H nằm giữa B và C (vì tam giác ABC nhọn)

    Xét tam giác ABH vuông tại H có:

    BH = AB.cosB = c.cosB

    Xét tam giác ACH vuông tại H có:

    CH = AC.cosC = b.cosC

    ⇒ a = BH + CH = c.cosB + b.cosC

Bài 5:

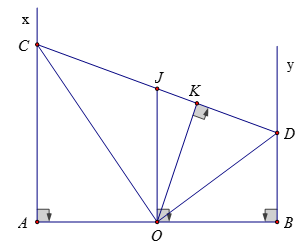
    Kẻ OJ ⊥ AB tại O; OK ⊥ CD tại K

    ⇒ OJ // AC // BD và JC = JD = OJ = CD/2

    ΔCJO cân tại J

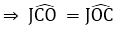
    Lại có:

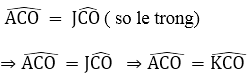
    Xét ΔACO và ΔKCO có:

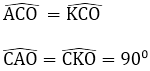
    CO : cạnh chung

    ⇒ ΔACO = ΔKCO (cạnh huyền – góc nhọn)

    ⇒ AC = CK; KO = AO = ½ AB ( O là trung điểm của AB)

    Chứng minh tương tự, ta có: KD = DB

    Xét tam giác vuông COD có:

    KO² = KC.KD = AC.BD

    ⇔ 1/4.AB² = AC.BD ⇔ 4AC.BD = AB²

Bài 6:

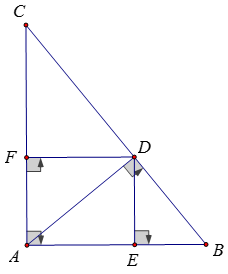
    Xét tam giác ADB vuông tại D có DE là đường cao nên

    EA.EB = DE²

    Xét tam giác ADC vuông tại D có DF là đường cao nên

    FA.FC = DF²

    ⇒ EA.EB + FA.FC = DE² + DF² = DE² + AE² = AD²

    Xét tam giác ABC vuông tại A có AD là đường cao nên

    DC.DB = AD²

    Do đó: EA.EB + FA.FC = DC.DB